
|
今天继续给大家分享排序算法里面的另外一种排序算法:归并排序!
一、归并排序: 1、归并排序操作的核心思想:
a、确定分界点:mid=(l+r)/2 b、递归排序左边和右边(排完左右两边的数,就会成为两个有序的序列了) c、归并(把上面的两个有序序列合并成一个有序的序列,用一个简单的词来说,就是合二为一!) 2、举例:
比如上图我们有两组已经排好的序列数字,我们要进行第三步合并,该如何进行呢?思路如下: a、这里先定义一个空的数组res,它主要是为了临时存放合并序列排序好的数字;我们从图中可以看到,第一个序列指针i指向数字1,第二序列指针j指向2,这个时候我们要比较两个数字的大小,小的数字就放到临时数组res里面去,这里我们明显知道数字1小于2,所以把1放到临时数组res里去 b、然后指针i往下移动,如下图所示,再次进行比较,明显发现指针j指向的数字2更小,把它放到res里面去,然后指针j往下移动,指针i不动,后面依次类推 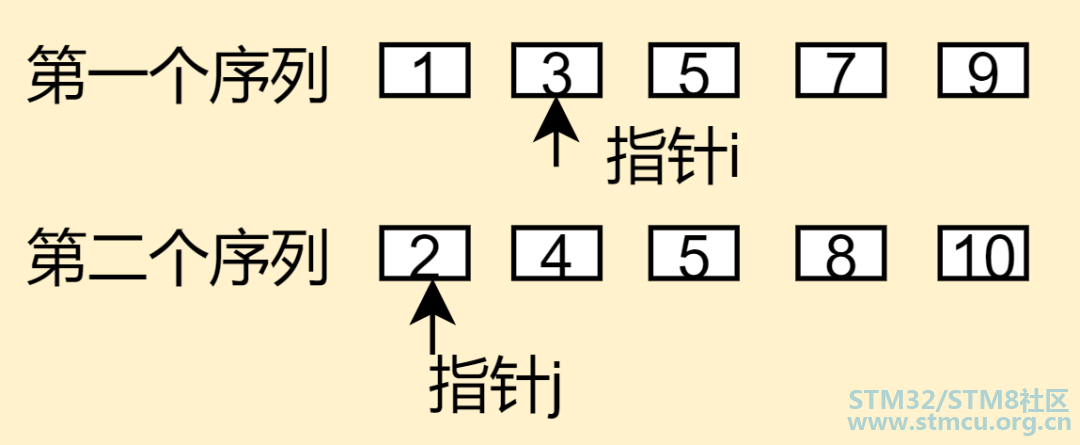
c、如下图所示,两个指针都指向了数字5,如果遇到两个数字一样的话,一般是把第一个序列的数字放到临时数组res里面去,这点稍微要注意一下
d、最后把临时数组里面的是数字放到原来的数组里面去 注意:一个算法稳定,并不能说它的时间效率是稳定的;这里的稳定是说两个序列中有两个数是相同的,如果在排完序之后,他们的位置还是没有发生变化的话,那么这个排序就是稳定的,反之亦然! 3、归并排序的平均时间复杂度的计算推导: 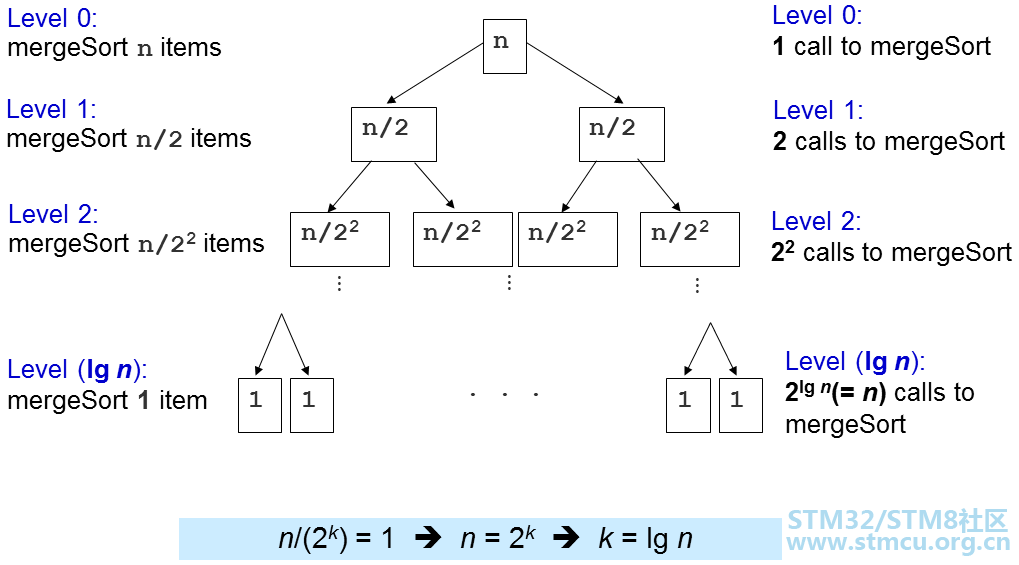
从图片的纵性来分析,当拆解到1的时候,这个时候什么数等于n除于它等于1,通过计算,我们知道是logn,然后再从横向分析,我们要最多比较n个数字,所以归并排序的时间复杂度就是:nlogn 二、代码示例:
代码: #include <iostream>using namespace std; const int N = 1e5 + 10; int n; int q[N], tmp[N]; void merge_sort(int q[],int l, int r) { if(l>=r)return;//判断序列中是否为空或者只有一个数字,如果是的话,我们就不用排序了 //确定分界点 int mid = l + r >> 1; //递归处理 merge_sort(q,l,mid); merge_sort(q,mid+1,r); //定义双指针 int k =0,i = l, j= mid+1; //归并处理 while(i <= mid && j <= r) if(q < q[j])tmp[k++] = q[i++]; else tmp[k++] = q[j++]; //把源数组中剩余的数字(注意这里的数字一定是最小的)放到临时数组后面去 while(i <= mid)tmp[k++] = q[i++]; while(j <= r)tmp[k++] = q[j++]; //把临时数组中排好序的数字放到源数组中去 for(i = l, j =0;i<=r;i++,j++)q=tmp[j]; } int main() { scanf("%d",&n); for(int i = 0;i<n;i++) { scanf("%d",&q); } merge_sort(q,0,n-1); for(int i = 0; i<n;i++) { printf("%d ",q); } return 0; } 结果:
最后来一个更加生动形象的归并排序演示视频(来源:https://visualgo.net/en/sorting): https://mp.weixin.qq.com/s/iadRSR7EmvxAKM65oMmJTg |
 微信公众号
微信公众号
 手机版
手机版
