特别说明：完整45期数字信号处理教程，原创高性能示波器代码全开源地址：链接
3 N! j4 x5 {. `6 R" H" Z% j7 a

第18章 ComplexMathFunctions的使用（二）

6 f6 u( Z8 r/ _8 R8 s; J3 z' L4 D

    本期教程主要讲解复数运算中的模平方，复数乘法和复数乘实数的求解。

    18.1 复数模平方 ComplexMagSquared

    18.2 复数乘法 ComplexMultComplex

    18.3 复数乘实数 ComplexMultComplex

    18.4 总结

18.1 复数模平方 ComplexMagSquared18.1.1 arm_cmplx_mag_squared_f32

公式描述：

    for(n=0; n<numSamples; n++) {        

            pDst[n] = pSrc[(2*n)+0]^2 + pSrc[(2*n)+1]^2;        

     }  

函数定义如下：

    void arm_cmplx_mag_squared_f32(float32_t * pSrc, float32_t * pDst, uint32_t numSamples)

参数定义：

    [in]  *pSrc   points to the complex input vector        

    [out]  *pDst  points to the real output vector        

    [in]  numSamples  number of complex samples in the input vector  

注意事项：

    1. 数组pSrc和pDst中存储的数据格式是（实部，虚部，实部，虚部……………）

18.1.2 arm_cmplx_mag_squared_q31

公式描述：

    for(n=0; n<numSamples; n++) {        

            pDst[n] = pSrc[(2*n)+0]^2 + pSrc[(2*n)+1]^2;        

     }  

函数定义如下：

    void arm_cmplx_mag_squared_q31(q31_t * pSrc, q31_t * pDst, uint32_t numSamples)

参数定义：

    [in]  *pSrc   points to the complex input vector        

    [out]  *pDst  points to the real output vector        

    [in]  numSamples  number of complex samples in the input vector  

注意事项：

    1. 数组pSrc和pDst中存储的数据格式是（实部，虚部，实部，虚部……………）

* g6 u( _% w& l18.1.3 arm_cmplx_mag_squared_q15

公式描述：

    for(n=0; n<numSamples; n++) {        

            pDst[n] = pSrc[(2*n)+0]^2 + pSrc[(2*n)+1]^2;        

     }  

函数定义如下：

    void arm_cmplx_mag_squared_q15(q15_t * pSrc, q15_t * pDst, uint32_t numSamples)

参数定义：

    [in]  *pSrc   points to the complex input vector        

    [out]  *pDst  points to the real output vector        

    [in]  numSamples  number of complex samples in the input vector  

注意事项：

    1. 数组pSrc和pDst中存储的数据格式是（实部，虚部，实部，虚部……………）

/ ^- i8 R; @9 e5 p18.1.4 实例讲解

实验目的：

     1. 学习ComplexMathFunctions中模平方的求解

实验内容：

    1. 按下按键K1, 串口打印函数DSP_MagSquared的输出结果

实验现象：

    通过窗口上位机软件SecureCRT（V5光盘里面有此软件）查看打印信息现象如下：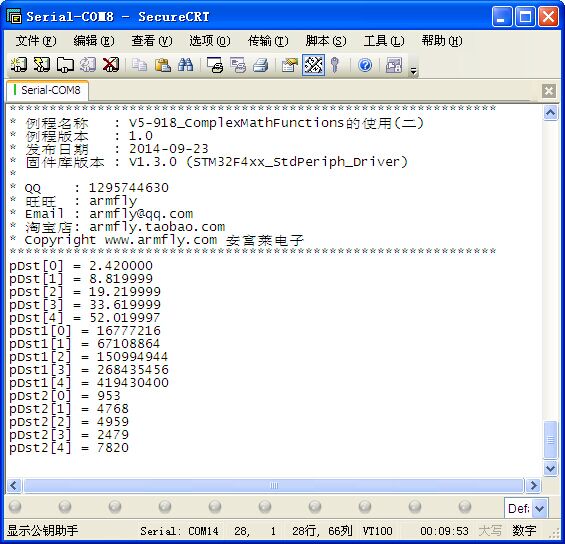

程序设计：

1. /*
   1 x+ z' y6 v; m+ o8 Z
2. *********************************************************************************************************
   . g6 L/ L" E1 M7 a' M
3. *        函 数 名: DSP_MagSquared
   ) a& g& \" a4 Y! ~2 z; a1 k* w
4. *        功能说明: 复数模的平方
   
5. *        形    参：无
   - r& d5 n" y  z& _& r
6. *        返 回 值: 无
   
7. *********************************************************************************************************
   
8. */
   
9. static void DSP_MagSquared(void)
   6 i0 O: f5 u! O  x: q  c
10. {
    
11. uint8_t i;
    
12. float32_t pSrc[10] = {1.1f, 1.1f, 2.1f, 2.1f, 3.1f, 3.1f, 4.1f, 4.1f, 5.1f, 5.1f};
    + M: N( R" U' S, s) h. Z
13. float32_t pDst[10];
    
14. q31_t pSrc1[10] = {1*268435456, 1*268435456, 2*268435456, 2*268435456, 3*268435456, 3*268435456,
    
15.                     4*268435456, 4*268435456, 5*268435456, 5*268435456};
    
16. q31_t pDst1[10];
    % f# @+ M2 F! U. i
17. 
    2 C4 @2 t0 T' N% K3 ]5 a" d# Y
18. q15_t pSrc2[10] = {5000, 10000, 15000, 20000, 25000,  5000, 10000, 15000, 20000, 25000};
    
19. q15_t pDst2[10];
    5 I' @& d6 Z7 k0 }/ u
20. /***浮点数模平方*******************************************************************************/
    
21. arm_cmplx_mag_squared_f32(pSrc, pDst, 5);
    ' y7 g/ l; m( A3 L
22. for(i = 0; i < 5; i++)
    9 k4 j5 S: w2 ^7 ^1 {3 b+ M5 ?
23. {
    5 e% E8 k% ^2 ~1 l* F, c% }4 L4 D
24. printf("pDst[%d] = %f\r\n", i, pDst[i]);
    3 _. @* v1 x3 _( L0 W" p
25. }
    6 b1 ?. T# K2 n+ z3 I
26. /***定点数模平方Q31*******************************************************************************/
    . {4 ~7 e/ V, |
27. arm_cmplx_mag_squared_q31(pSrc1, pDst1, 5);
    & v5 w) i  z1 r% C; b% z& B. h
28. for(i = 0; i < 5; i++)
    
29. {
    + e. F) H7 l; b9 W! A8 q
30. printf("pDst1[%d] = %d\r\n", i, pDst1[i]);
    0 n, S4 |6 x  d1 \4 P7 B7 K: s3 ^
31. }
      Z1 V8 I$ y, H1 v) r4 r
32. /***定点数模平方Q15*******************************************************************************/
    
33. arm_cmplx_mag_squared_q15(pSrc2, pDst2, 5);
    
34. for(i = 0; i < 5; i++)
    4 V( b/ n5 |1 |8 |2 }
35. {
      G" I  D$ w+ F) @8 T
36. printf("pDst2[%d] = %d\r\n", i, pDst2[i]);
    5 |% U2 X1 `1 L+ Y2 r
37. }
    
38. }

复制代码

0 x. [& U# z. C9 i5 d

18.2 复数乘法 ComplexMultComplex

18.2.1 arm_cmplx_mult_cmplx_f32

公式描述：

    for(n=0; n<numSamples; n++) {        

            pDst[(2*n)+0] = pSrcA[(2*n)+0] * pSrcB[(2*n)+0] - pSrcA[(2*n)+1] * pSrcB[(2*n)+1];        

            pDst[(2*n)+1] = pSrcA[(2*n)+0] * pSrcB[(2*n)+1] + pSrcA[(2*n)+1] * pSrcB[(2*n)+0];        

    }  

函数定义如下：

    void arm_cmplx_mult_cmplx_f32(

      float32_t * pSrcA,

         float32_t * pSrcB,

        float32_t * pDst,

        uint32_t numSamples)

参数定义：

    [in]  *pSrcA   points to the first input vector        

    [in]  *pSrcB   points to the second input vector        

    [out]  *pDst   points to the output vector        

    [in]  numSamples number of complex samples in each vector   

注意事项：

    1. 数组pSrcA, pSrcB和pDst中存储的数据格式是（实部，虚部，实部，虚部……………）

  e; |3 F; s' n# q5 U  P18.2.2 arm_ cmplx_mult_cmplx_q31

公式描述：

    for(n=0; n<numSamples; n++) {        

            pDst[(2*n)+0] = pSrcA[(2*n)+0] * pSrcB[(2*n)+0] - pSrcA[(2*n)+1] * pSrcB[(2*n)+1];        

            pDst[(2*n)+1] = pSrcA[(2*n)+0] * pSrcB[(2*n)+1] + pSrcA[(2*n)+1] * pSrcB[(2*n)+0];        

    }

函数定义如下：

    void arm_cmplx_mult_cmplx_q31(

        q31_t * pSrcA,

        q31_t * pSrcB,

        q31_t * pDst,

        uint32_t numSamples)

参数定义：

    [in]  *pSrc   points to the complex input vector        

    [out]  *pDst  points to the real output vector        

    [in]  numSamples  number of complex samples in the input vector  

注意事项：

    1. 数组pSrcA, pSrcB和pDst中存储的数据格式是（实部，虚部，实部，虚部……………）

0 W* b) _# ~, G) s* `18.2.3 arm_cmplx_mult_cmplx_q15

公式描述：

    for(n=0; n<numSamples; n++) {        

            pDst[(2*n)+0] = pSrcA[(2*n)+0] * pSrcB[(2*n)+0] - pSrcA[(2*n)+1] * pSrcB[(2*n)+1];        

            pDst[(2*n)+1] = pSrcA[(2*n)+0] * pSrcB[(2*n)+1] + pSrcA[(2*n)+1] * pSrcB[(2*n)+0];        

    }   

函数定义如下：

    void arm_cmplx_mult_cmplx_q15(

        q15_t * pSrcA,

        q15_t * pSrcB,

        q15_t * pDst,

        uint32_t numSamples)

参数定义：

    [in]  *pSrc   points to the complex input vector        

    [out]  *pDst  points to the real output vector        

    [in]  numSamples  number of complex samples in the input vector  

注意事项：

    1. 数组pSrcA, pSrcB和pDst中存储的数据格式是（实部，虚部，实部，虚部……………）

18.2.4 实例讲解

实验目的：

    1. 学习ComplexMathFunctions中复数乘法的求解

实验内容：

    1. 按下按键K2, 串口打印函数DSP_CmplxMult的输出结果

实验现象：

    通过窗口上位机软件SecureCRT（V5光盘里面有此软件）查看打印信息现象如下：

程序设计：

1. /*
   2 k/ ]! L2 W; N( P! F) v1 Z. n
2. *********************************************************************************************************
   
3. *        函 数 名: DSP_CmplxMult
   ( w7 k1 G  w6 |: {
4. *        功能说明: 复数乘法
   " u$ E- g/ S9 e4 F+ k9 ^
5. *        形    参：无
   & H! r; a  I0 D  O7 I
6. *        返 回 值: 无
   
7. *********************************************************************************************************
   
8. */
   
9. static void DSP_CmplxMult(void)
   " ]0 [' a8 h  |9 j- d
10. {
    
11. uint8_t i;
    
12. float32_t pSrcA[10] = {1.1f, 1.2f, 2.1f, 2.2f, 3.1f, 3.2f, 4.1f, 4.2f, 5.1f, 5.2f};
    5 c; u4 n% _1 O7 J$ o# s5 ^3 Y
13. float32_t pSrcB[10] = {1.2f, 1.2f, 2.2f, 2.2f, 3.2f, 3.2f, 4.2f, 4.2f, 5.2f, 5.2f};
    
14. float32_t pDst[10];
    
15. q31_t pSrcA1[10] = {1*268435456, 1*268435456, 2*268435456, 2*268435456, 3*268435456, 3*268435456,
    * d3 Z' d& O$ ^" c8 I6 @
16.                     4*268435456, 4*268435456, 5*268435456, 5*268435456};
    
17. q31_t pSrcB1[10] = {1*268435456, 1*268435456, 2*268435456, 2*268435456, 3*268435456, 3*268435456,
    ' |3 r0 w2 g' {( s
18.                     4*268435456, 4*268435456, 5*268435456, 5*268435456};
    
19. q31_t pDst1[10];
    ) `6 ?! T, Q$ I2 G, X
20. q15_t pSrcA2[10] = {5000, 10000, 15000, 20000, 25000,  5000, 10000, 15000, 20000, 25000};
    4 Y$ J5 c, V: r+ L; U: d3 L
21. q15_t pSrcB2[10] = {6000, 11000, 15000, 20000, 25000,  5000, 10000, 15000, 20000, 25000};
    7 w- \4 U! B+ i- {; N& F
22. q15_t pDst2[10];
    
23. /***浮点数乘法*******************************************************************************/
    ! X0 P  H4 Q# n) e3 J4 H% L
24. arm_cmplx_mult_cmplx_f32(pSrcA, pSrcB, pDst, 5);
    
25. for(i = 0; i < 5; i++)
    
26. {
    
27. printf("pDst[%d] = %f %fj\r\n", i, pDst[2*i], pDst[2*i+1]);
    
28. }
      Q0 \4 ?6 a% F* T
29. /***定点数乘法Q31*******************************************************************************/
    ( Z2 v" ?; Y! W1 @, N9 j$ ~
30. arm_cmplx_mult_cmplx_q31(pSrcA1, pSrcB1, pDst1, 5);
    1 t1 M- R6 p2 p* v& ?
31. for(i = 0; i < 5; i++)
    
32. {
    
33. printf("pDst1[%d] = %d %dj\r\n", i, pDst1[2*i], pDst1[2*i+1]);
    
34. }
    ' q- B" I  r' h. B% z
35. /***定点数乘法Q15*******************************************************************************/
    : N  ]; |) Z7 _) l4 S  x# P+ D7 A. _
36. arm_cmplx_mult_cmplx_q15(pSrcA2, pSrcB2, pDst2, 5);
    
37. for(i = 0; i < 5; i++)
    
38. {
    
39. printf("pDst1[%d] = %d %dj\r\n", i, pDst2[2*i], pDst2[2*i+1]);
    
40. }
    
41. }

复制代码

* e  K! F/ e( O, ]9 w" Z# A
) q' i4 Z0 k: N

18.3 复数乘实数 ComplexMultComplex

" l, X0 {- @3 [! J+ m& \, `) e18.3.1 arm_cmplx_mult_cmplx_f32

公式描述：

    for(n=0; n<numSamples; n++) {        

           pCmplxDst[(2*n)+0] = pSrcCmplx[(2*n)+0] * pSrcReal[n];        

           pCmplxDst[(2*n)+1] = pSrcCmplx[(2*n)+1] * pSrcReal[n];        

     }   

函数定义如下：

    void arm_cmplx_mult_real_f32(

        float32_t * pSrcCmplx,

        float32_t * pSrcReal,

        float32_t * pCmplxDst,

        uint32_t numSamples)

参数定义：

     [in]  *pSrcCmplx   points to the complex input vector        

     [in]  *pSrcReal     points to the real input vector        

     [out]  *pCmplxDst  points to the complex output vector        

     [in]  numSamples  number of samples in each vector

注意事项：

    1. 数组pSrcCmplx, pCmplxDst中存储的数据格式是（实部，虚部，实部，虚部……………）

18.3.2 arm_ cmplx_mult_cmplx_q31

公式描述：

     for(n=0; n<numSamples; n++) {        

           pCmplxDst[(2*n)+0] = pSrcCmplx[(2*n)+0] * pSrcReal[n];        

           pCmplxDst[(2*n)+1] = pSrcCmplx[(2*n)+1] * pSrcReal[n];        

     }  

函数定义如下：

    void arm_cmplx_mult_real_q31(

        q31_t * pSrcCmplx,

        q31_t * pSrcReal,

        q31_t * pCmplxDst,

        uint32_t numSamples)

参数定义：

    [in]  *pSrcCmplx   points to the complex input vector        

    [in]  *pSrcReal     points to the real input vector        

    [out]  *pCmplxDst  points to the complex output vector        

    [in]  numSamples  number of samples in each vector

注意事项：

    1. 数组pSrcCmplx, pCmplxDst中存储的数据格式是（实部，虚部，实部，虚部……………）

18.3.3 arm_cmplx_mult_cmplx_q15

公式描述：

     for(n=0; n<numSamples; n++) {        

           pCmplxDst[(2*n)+0] = pSrcCmplx[(2*n)+0] * pSrcReal[n];        

           pCmplxDst[(2*n)+1] = pSrcCmplx[(2*n)+1] * pSrcReal[n];        

     }

函数定义如下：

    void arm_cmplx_mult_real_q15(

        q15_t * pSrcCmplx,

        q15_t * pSrcReal,

        q15_t * pCmplxDst,

        uint32_t numSamples)

参数定义：

    [in]  *pSrcCmplx   points to the complex input vector        

    [in]  *pSrcReal     points to the real input vector        

    [out]  *pCmplxDst  points to the complex output vector        

    [in]  numSamples  number of samples in each vector

注意事项：

    1. 数组pSrcCmplx, pCmplxDst中存储的数据格式是（实部，虚部，实部，虚部……………）

18.3.4 实例讲解

实验目的：

    1. 学习ComplexMathFunctions中复数乘法的求解

实验内容：

    1. 按下按键K3, 串口打印函数DSP_CmplxMultReal的输出结果

实验现象：

    通过窗口上位机软件SecureCRT（V5光盘里面有此软件）查看打印信息现象如下：

程序设计：

1. /*
   5 E& D, E2 j- n4 V& k6 n) w; D) [
2. *********************************************************************************************************
   
3. *        函 数 名: DSP_CmplxMultReal
   
4. *        功能说明: 复数乘实数
   & u. w/ `" I! U
5. *        形    参：无
   
6. *        返 回 值: 无
   * B/ d! ^  U% C0 r; N$ n- i0 l
7. *********************************************************************************************************
   
8. */
   , m3 Y* `. D1 k2 D2 l3 v
9. static void DSP_CmplxMultReal(void)
   
10. {
    
11. uint8_t i;
      p) {% V& p% D
12. float32_t pSrcCmplx[10] = {1.1f, 1.2f, 2.1f, 2.2f, 3.1f, 3.2f, 4.1f, 4.2f, 5.1f, 5.2f};
    # s4 n4 H: }+ h4 u: `
13. float32_t pSrcReal[5] = {1.2f, 1.2f, 2.2f, 2.2f, 3.2f};
    ! [9 M& ]5 r. N# _
14. float32_t pCmplxDst[10];
    
15. q31_t pSrcCmplx1[10] = {1*268435456, 1*268435456, 2*268435456, 2*268435456, 3*268435456, 3*268435456,
    
16.                     4*268435456, 4*268435456, 5*268435456, 5*268435456};
    
17. q31_t pSrcReal1[10] = {1*268435456, 1*268435456, 2*268435456, 2*268435456, 3*268435456};
    6 S! ^1 v& p) w& M' Q+ {/ Y8 X
18. q31_t pCmplxDst1[10];
    " ?# l" p4 @+ U6 T0 ^- z5 n; m) A
19. q15_t pSrcCmplx2[10] = {14000, 16000, 20000, 20000, 30000, 31000, 12000, 13000, 14000, 25000};
    ( W! w5 V/ u& H0 ?9 _
20. q15_t pSrcReal2[10] =  {15000, 17000, 20000, 20000, 30000};
    3 l0 i+ d% s8 ^2 ?* K- ]
21. q15_t pCmplxDst2[10];
    
22. /***浮点数*******************************************************************************/
    
23. arm_cmplx_mult_cmplx_f32(pSrcCmplx, pSrcReal, pCmplxDst, 5);
    
24. for(i = 0; i < 5; i++)
    
25. {
    ; T) j) G5 h  J
26. printf("pCmplxDst[%d] = %f %fj\r\n", i, pCmplxDst[2*i], pCmplxDst[2*i+1]);
    ) e7 r9 w: B6 r& Y% l+ X7 g) {
27. }
    * x0 h+ s$ `! C- N( P) {: f' k
28. /***定点数Q31*******************************************************************************/
    
29. arm_cmplx_mult_cmplx_q31(pSrcCmplx1, pSrcReal1, pCmplxDst1, 5);
    
30. for(i = 0; i < 5; i++)
    : p+ V5 M# v$ h
31. {
    
32. printf("pCmplxDst1[%d] = %d %dj\r\n", i, pCmplxDst1[2*i], pCmplxDst1[2*i+1]);
    0 a5 `0 {7 K, a, [& g& e# w
33. }
    8 O$ K8 Z4 f  t% U  O( M- [
34. /***定点数Q15*******************************************************************************/
    
35. arm_cmplx_mult_cmplx_q15(pSrcCmplx2, pSrcReal2, pCmplxDst2, 5);
    
36. for(i = 0; i < 5; i++)
    $ P* n2 b6 ?/ V2 X# p
37. {
    
38. printf("pCmplxDst2[%d] = %d %dj\r\n", i, pCmplxDst2[2*i], pCmplxDst2[2*i+1]);
    
39. }
    
40. }

复制代码

18.4 总结

    本期教程就跟大家讲这么多，有兴趣的可以深入研究下算法的具体实现。

& ?& s5 n: |1 Z! p

学习了啊

好好的学习下！

正在学习中，顶一下