|
基于STM32和PID算法的小车车速控制 ( Z4 M/ q" v* b; D 四轴飞行器飞行原理与双闭环PID控制 5 u, [$ M9 D/ T+ i* w& d2 M5 U PID程序实例 + Z$ j k/ P) ^) R- n" }$ U1 Z# ^* g ! f$ g+ M+ S# l2 m& R 该文档总结于以下两个博文：: @1 d/ y4 R" ]( T http://www.moz8.com/thread-36004-1-1.html 和http://www.eeboard.com/bbs/thread-32321-1-3.html6 d$ F0 u4 s5 p2 {0 D Q 5 Q5 W; r* X- k+ i# x; S4 L 为了更好的理解这个视频和PID参数的作用，特意根据多轴飞行器的原理和PID理论，编写了一个EXCEL图表，直观的来理解PID参数的作用。, N6 V- l: j. t2 n 在这个模型中： 1、假设输出是力，作用在一个质块上，使用加速度、速度、位移积分计算，评估输出对测量值产生的影响，跟多轴飞行器的运动模式比较接近。 2、让速度响应慢一个拍子，模拟电调和电机的响应滞后。 3、加入阻尼，模拟空气的衰减作用) a7 P* W9 S j( ^ 4、引入偏差，用于体现I的作用，从中间加入，代表一个系统误差或外作用力 # G( y3 B) D& c# k PID的作用概述：4 b, V# n. D' d& A+ c* P/ Z4 ` 1、P产生响应速度和力度，过小响应慢，过大会产生振荡，是I和D的基础。 2、I在有系统误差和外力作用时消除偏差、提高精度，同时也会增加响应速度，产生过冲，过大会产生振荡。. I/ }2 s( Z+ C' Y+ D 3、D抑制过冲和振荡，过小系统会过冲，过大会减慢响应速度。D的另外一个作用是抵抗外界的突发干扰，阻止系统的突变。 通过这个模型和图表，一步步演示PID参数的作用和调试方法： 1、逐步增大P，看P对响应速度和力度的影响，调到系统发生振荡，再减少一点P3 R. I n! d* y8 F6 | v9 u: y% ^ - n+ L, Y& _9 H 当P=0.1时，响应很慢，但不会振荡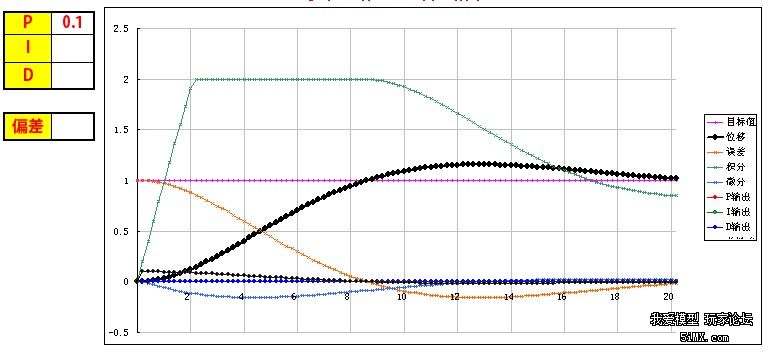: B, n' @3 E8 S5 T& h0 V" D- R9 q  粗黑线是系统响应，洋红线是目标值。* D0 U q" h7 r- N- Z% } 逐步增大P，P=1，有振荡，但慢慢在衰减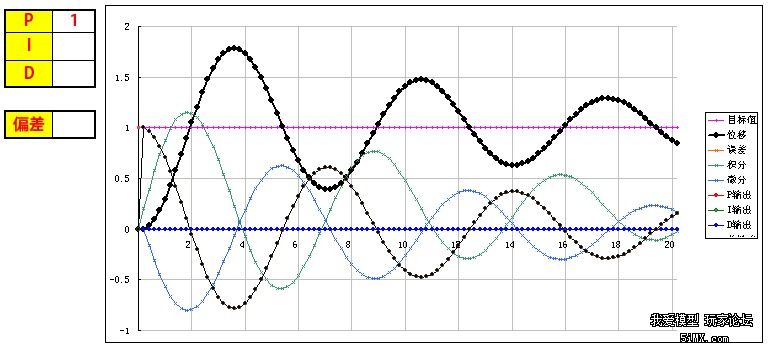8 ?. W% r9 Z- K' q5 F! a  ) }2 D" M) R) H4 c+ N 继续增大P，P=3，振荡会逐步加大  取振荡但会衰减的P=1继续调整& n) w9 f8 f( T0 n 在多轴调试时，当振荡发生时，再稍微减小一点P。" D( {) k+ S* ]7 p 2、加入D，看D对振荡的控制能力，D过小会发生过冲，D过大会迟滞，以稍微有点过冲为最佳4 u/ c; N. G x# q2 R D=0.5，有较大的过冲和少量振荡，衰减很快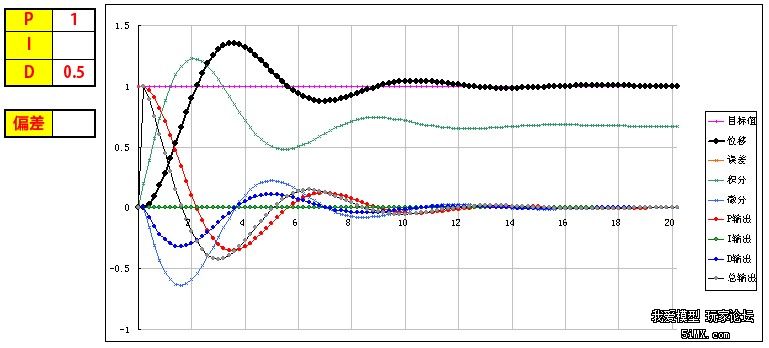8 O0 \8 u* L# M' q! t  # {( R% O2 ^% n' t, Z% y4 U+ d% _D=1.3，基本没过冲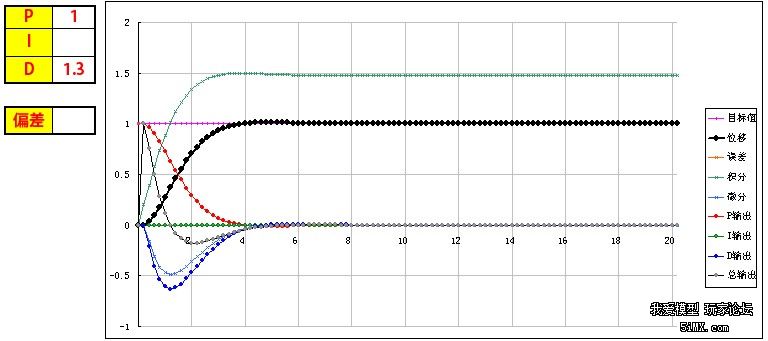5 z9 k3 |: Y5 B6 `9 S% J1 f' e. w  D=2，响应迟滞，减慢了响应速度  4 q& `& ^% `5 ? m6 @取以稍微有点过冲的D=1.3为最佳 在多轴调试时，用手拍一下机臂或倾斜启动，机臂在复位时有少量过冲为宜。（不过我喜欢基本没过冲时的参数，这样在悬停时更稳）) K3 ?# [4 k( B0 `, K/ j : d. S! `: Y2 w/ _8 b 3、可以继续增大P和D，让响应更快但过冲也不大。 P=2 D=1.8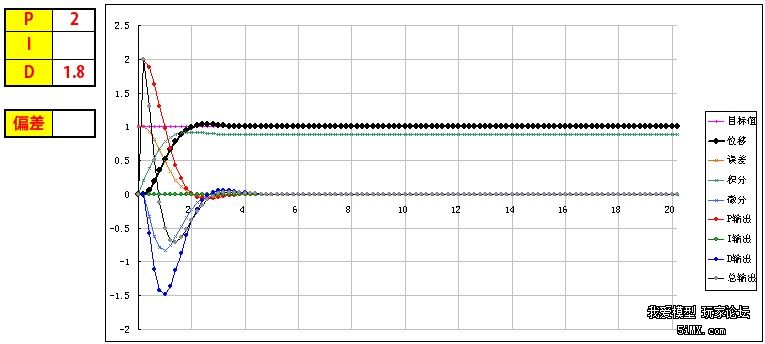# V/ [$ q" c! J  ; X. x( L" j+ v2 O" H 在理论上可以这样演示，但在实际多轴的调试时，这一步一般不做，这是为了更安全和稳定。 0 p8 y' e1 S( _# D2 n, Q9 N( ` 4、加入0.2的偏差，看偏差对位移的影响 从中间加入，代表一个外作用力。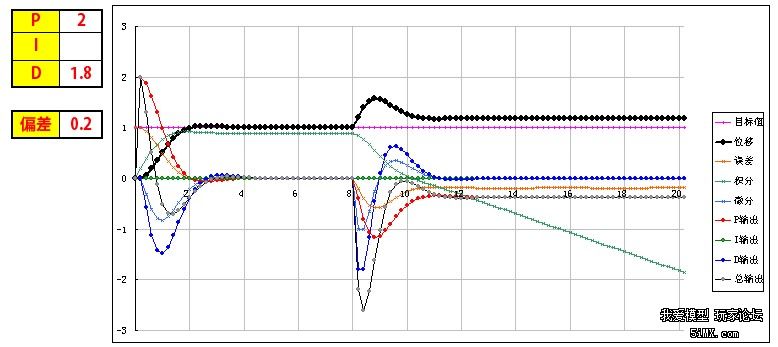5 `( b! _+ f: @9 r  + w3 s( v0 `# Q( @8 U可以看到，如果没有I的作用，偏差将一直存在，尽管P产生了一个抵抗力，但只是阻止了系统继续运动，但偏差一直在。 在多轴调试时，如果持续的抬起一个机臂，机臂会持续的转动，抵抗力很小，放手后也不会回复。6 @* f: }; r7 C1 c, ? 5、加I,看I对偏差的修正能力，I加快了响应速度，但也会导致过冲或振荡9 u- Y# b! t3 N/ ?4 Z; x/ D I=0.3 基本可以消除偏差产生的影响，产生了少量过冲，但提高了在有偏差时系统的精度 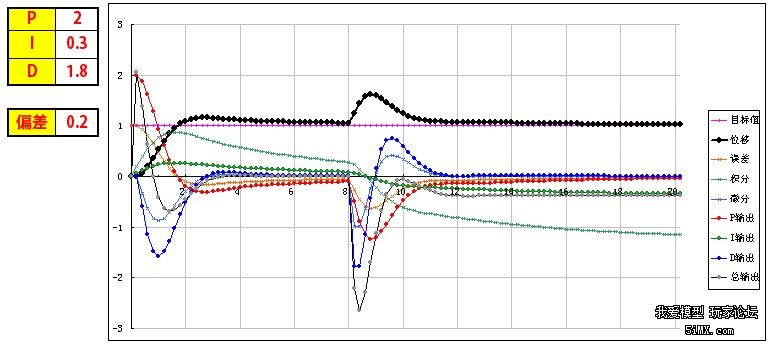 / \6 x/ J1 g& x/ e- ~; B6 x8 S/ G I=3 进一步加快响应速度，但产生了振荡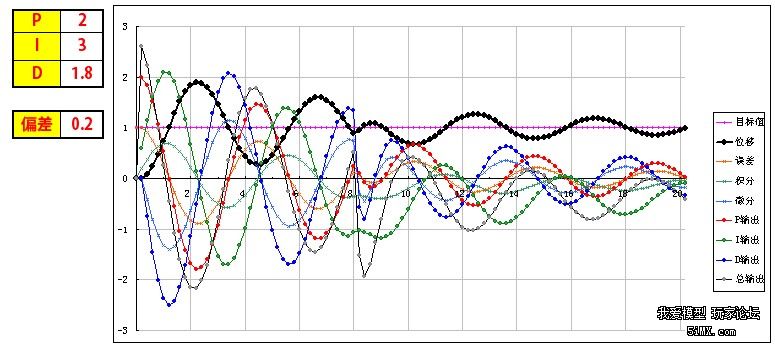4 A) X b0 q w: E2 {' J- M4 u6 `  ; d4 D4 I% b- L: t8 \) \取基本能纠正偏差的I=0.3- \6 |% f* w# k) P3 x% H 在多轴调试时，油门开至悬停油门，用手持续的抬起一个机臂，可以感到随着I的增加，抵抗力会逐步增大，持续时间加长。0 F+ n$ h8 Z2 n$ g' E& x 因为多轴的长期稳定由姿态模式的LEVEL参数来解决，所以I不用太大，取缺省参数就可以了，大概可以抵抗1-2秒左右。& \6 B! j) y G $ F6 w# X, P4 p3 a8 [# X 6、增大一点D，减小一点I产生的过冲 取消偏差，因为I的加入，有一点过冲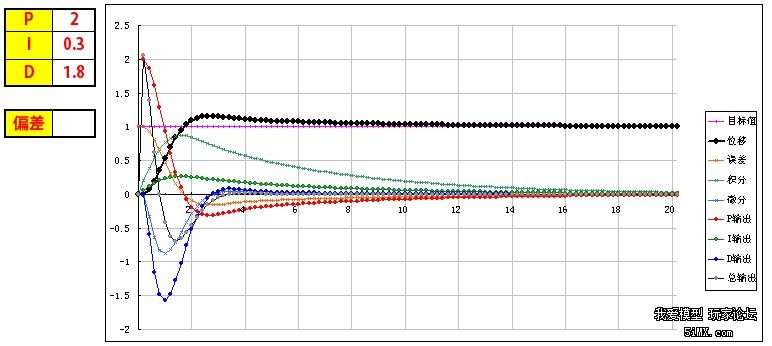! I6 E. O1 u3 ^; f; E4 l  & \5 x/ L( }* y* C/ S2 I* }" u5 |. _+ w8 L& e 增大D，D=2.2，减小过冲 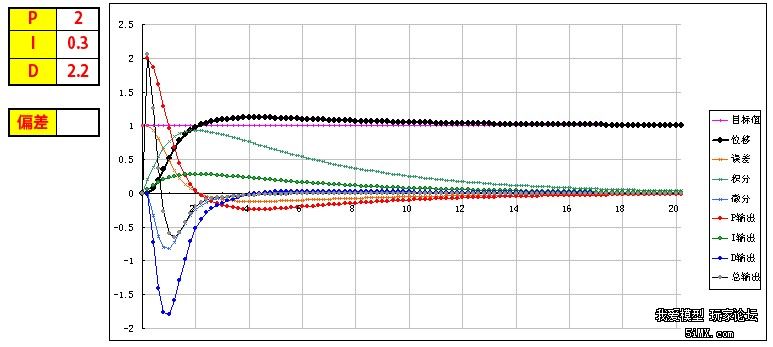 6 Y5 P/ T7 f. x1 |% E) b: B" }& ~9 h# g* ]1 H4 D 在实际多轴调试时，这一步一般不用，但是如果有必要，可以试一下。( Q7 Z* s6 K. N1 E8 S/ h 好了，曲线演示完了，这同时也是多轴PID参数的调试过程，结合视频一起看，能更好的理解这一过程，希望对大家理解PID有所帮助。3 k$ S3 c1 s& w $ O2 R p. g/ V) i 附：多轴飞行器PID调试演示器.xls5 I" j: s$ Z8 ]( \9 ~" g 4 `8 J1 p1 p& G# E& P8 I 另外，试了一下，下载的文件名可能有问题，自己把文件名改为"多轴飞行器PID调试演示器.xls"就可以用了 2 i. l3 X, k) o6 ]( a$ m PID的代码其实也很简单，主要是要了解其中的原理，才能更好地调整参数。为了方便新手们理解，楼主建立了一个数学模型来让大家了解。（只针对新手，老手就算了)8 M! E0 V/ z {; O! n+ m . a- \9 Z& s% X; D) I ========圆点博士小四轴之PID控制模式分析=======+ q2 k8 ^4 K* u+ ]. K PID控制的P是Proportional的缩写, 是比例的意思，I是Integral的缩写，是积分的意思，D是Derivative的缩写，是微分的意思。所以，PID就是我们常说的比例，积分，微分控制。 我们首先来看一个PID控制模型曲线图：& Y. m$ o0 ]7 v) i9 ] 该图包含了比例控制，比例+积分控制，比较+积分+微分控制的电机响应图的对比。 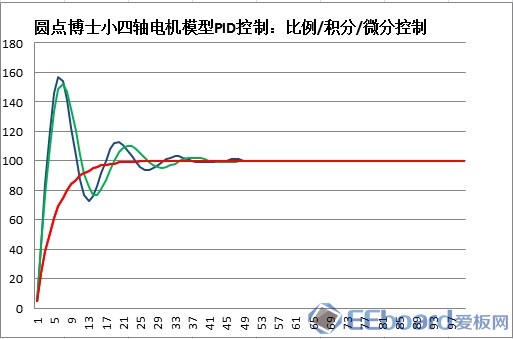3 s7 B: H$ v U# e5 a" e: X5 A  2014-5-29 13:22 上传下载附件 (37.76 KB) PID模型 0 R3 C# p! u: d- r# Y3 n w% ~( U" u# l, P3 p6 u7 m, I! h0 L 下面我们对曲线进行具体分析：$ f8 y* Y& p; ?: [8 \- e2 w. f PID中的比例控制是最容易理解的，比例控制就是把角度的误差乘以一个常数作为输出驱动。假定我们有一个理想模型的电机，1V电压的变化会带来小四轴1度的角度改变。假定现在电机控制电压是5V,小四轴在某一轴上的偏角是5度，目标角度是100度。我们把当前的电压量定义为Vin,把输出控制量定义为Vout。假定P等于0.2，那么比例控制的结果就是： 第一次：Vout=Vin+(100-5)*P=5V+19V=24V，得到电机电压是24V，对应的小四轴角度是24度,距离目标角度的误差是100-24=76度。 第二次：Vout=Vin+(100-24)*P=24V+15V=39V, 从而引起的角度是39度。, P- w6 P* h8 z, V7 o! s 我们看到，在这么的一个比例控制系统下，小四轴角度在慢慢地向目标角度靠近。 / Z6 |, O- |4 p5 [* }4 o; d( j PID中的积分控制就是把把所有角度误差相加起来，然后乘上一个常数作为输出驱动。在上述例子中，假定I=0.2, 我们来看看比例和积分控制同时起作用下的系统反应。 第一次：Vout=Vin+(100-5)*P+(100-5)*I=5V+19V+19V=43V，这时候小四轴角度为43度。 由于第一次控制前的误差是100-5=95,第二次控制前的误差是100-43=57，所以积分结果是152。 第二次：Vout=Vin+(100-43)*P+((100-5)+(100-43)）*I=43V+11V+30V=84V, 这时候小四轴角度变为84度。 第三次：Vout=Vin+(100-84)*P+((100-5)+(100-43)+（100-84））*I=84+3V+33V=120V。这时小四轴角度变为120度。4 R5 g" g8 c3 u. _# T 我们看到，在增加了积分控制后，小四轴角度在快速向目标角度靠近。2 {2 I# S8 j, a6 L$ C9 p ' v' _. l2 w' l& L3 T7 V3 c/ n PID中的微分控制就是把角度的变化乘上一个常数来作为电机驱动输出。在上述例子中，假定D=0.2, 我们来看看比例,积分和微分共同控制下的系统反应。假定第一次前，电机转速保持5转，那么第一次前的角度变化为0。 ^ i6 e: @& E+ p1 o6 W, J6 \ w 第一次：Vout=Vin+(100-5)*P+(100-5)*I-（5-5）*D=5V+19V+19V-0V=43V，这时候小四轴角度为43度。+ Q. q# V8 g* V6 ` 和上一次相比，角度从5度变化到了43度，所以小四周角度变化是43-5=38度。 第二次：Vout=Vin+(100-43)*P+((100-5)+(100-43)）*I-（43-5）*D=43V+11V+30V-7V=77V, 这时候小四周角度77度。 2 U j2 c2 O& U4 w; _8 L 把上述的计算结果列出来，我们看到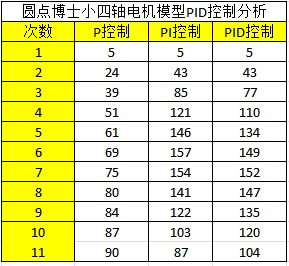：  2014-5-29 13:23 上传5 d* F/ @ m8 _; A7 v$ p下载附件 (39.13 KB) + ?7 K2 q6 \1 w. L PID计算 ' b, d; a& G* \3 {9 g * u1 V& g2 U$ S7 a2 n $ P4 @7 L4 F5 @$ |0 B' {* ]/ j * ]0 g0 u m" } J# O 从上面的数据，我们可以看到：* J' D/ r! C2 E3 p% V- y 1，单独比例控制的时候，数据慢慢接近目标 （图表中的红色线） 2，加入积分控制之后，数据快速接近目标 （图表中的蓝色线） 3，微分控制起到抑制变化的作用。（图表中的绿色线） & H9 W7 x" k) O+ K, d5 Z; V 有了这些理论基础，就可以写PID控制代码拉。- |) w7 L, q; t, O2 O% @6 E ! X0 S W8 h" ]* P; }0 q/ n |
PID.zip
下载23.06 KB, 下载次数: 1561
微信公众号
手机版
中级的pid调节，需要根据控制模型建模，然后零极点对消，等效1型或2型系统，根据最佳整定法计算pi参数，这是掌握一些自控原理的基础了。
高级一些的应该都是用自抗扰控制器，抗饱和积分(anti-windup)等，尤其是飞行器。