特别说明：完整45期数字信号处理教程，原创高性能示波器代码全开源地址：链接

第10章 FastMathFunctions的使用

' Y2 G/ z3 Z0 A

    本期教程开始，我们将不再专门的分析DSP函数的源码，主要是有些DSP函数的公式分析较麻烦，有兴趣的同学可以自行研究，本期教程开始主要讲解函数如何使用。

    10.1 三角函数Cosine

    10.2 三角函数Sine

    10.3 平方根Sqrt

    10.4 实例讲解（Matlab验证）

    10.5 总结

1 g8 u  u; F; y5 n5 H10.1 三角函数Cosine

    三角函数cosine的计算是通过查表并配合三次插补实现的。具体的实现方法大家可以查阅相关资料进行了解。

10.1.1 arm_cos_f32

    此函数的使用比较简单，函数定义如下：

     float32_t  arm_cos_f32(float32_t x)

注意输入参数x是弧度制即可，也就是说cos函数的一个周期对应于弧度[ 0  2*PI）。下面我们先通过Matlab绘制一个周期的cos曲线。新建一个.m格式的脚本文件，并写入如下函数：

           x = 0:0.01:2*pi;

           plot(x, cos(x))

运行后显示效果如下：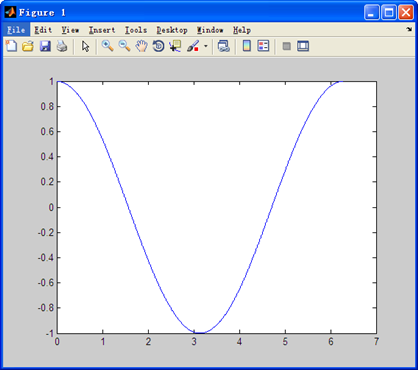

点击上面截图中的Tools->Data statistics，获取数据的分析结果，我们主要看Y轴。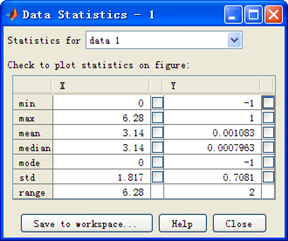

最大值和最小值分别对应1和-1，这个与我们所学的理论知识是相符的。

10.1.2 arm_cos_q31

    函数定义如下：

      q31_t  arm_cos_q31(q31_t x)

    使用中只需注意参数x的数值范围[0 2^31）相当于弧度[0 2*PI)即可。

10.1.3 arm_cos_q15

    函数定义如下：

      q31_t  arm_cos_q15(q15_t x)

    使用中只需注意参数x的数值范围[0 2^15）相当于弧度[0 2*PI)即可。

10.2 三角函数Sine

    三角函数sine的计算是通过查表并配合三次插补实现的。具体的实现方法大家可以查阅相关资料进行了解。

10.2.1 arm_sine_f32

    此函数的使用比较简单，函数定义如下：

       float32_t arm_sin_f32(float32_t x)

注意输入参数x是弧度制即可，也就是说sine函数的一个周期对应于弧度[ 0  2*PI）。下面我们先通过Matlab绘制一个周期的sine曲线。新建一个.m格式的脚本文件，并写入如下函数：

            x = 0:0.01:2*pi;

            plot(x, sine(x))

运行后显示效果如下：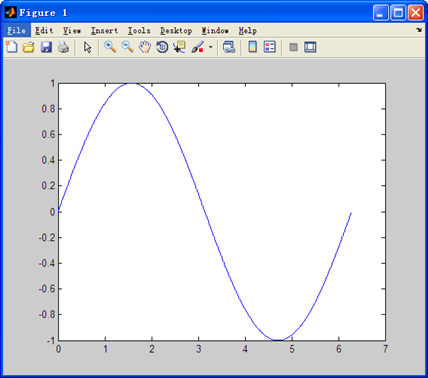

点击上面截图中的Tools->Data statistics，获取数据的分析结果，我们主要看Y轴。

最大值和最小值分别对应1和-1，这个与我们所学的理论知识是相符的。

10.2.2 arm_sin_q31

    函数定义如下：

       q31_t  arm_sin_q31(q31_t x)

    使用中只需注意参数x的数值范围[0 2^31）相当于弧度[0 2*PI)即可。

10.2.3 arm_sin_q15

    函数定义如下：

       q31_t  arm_sin_q15(q15_t x)

    使用中只需注意参数x的数值范围[0 2^15）相当于弧度[0 2*PI)即可。

10.3 平方根sqrt

    浮点数的平方根计算只需调用一条浮点指令即可，而定点数的计算要稍显麻烦。

10.3.1 arm_sqrt_f32

     对于CM4带FPU的处理器来说，浮点数的平方根求解很简单，只需调用指令__sqrtf，仅需要14个时钟周期就可以完成。函数定义如下（在arm_math.h里面）：

                     static __INLINE arm_status arm_sqrt_f32(float32_t in, float32_t * pOut)

10.3.2 arm_sqrt_q31

    函数的定义如下：

     arm_status arm_sqrt_q31(q31_t in, q31_t * pOut)

    这里in的输入范围是0x00000000 到 0x7FFFFFFF，转化成浮点数范围就是[0 +1)。在使用这个函数的时候有一点要特别的注意，比如我们要求1000的平方根，而获得结果是1465429，这是为什么呢，分析如下：

    定点数1000 = 浮点数 1000 /(2^31) = 4.6566e-07 (用Q31表示)。

              对4.6566e-07求平方根可得 6.8239e-04。

        定点数1465429 = 浮点数 1465429/(2^31)  =  6.8239e-04。

简单的总结下上面的意思就是说，求定点数1000的平方根，实际是求浮点数4.6566e-07 (用Q31表示)的平方根。

10.3.3 arm_sqrt_q15

    函数的定义如下：

          arm_status arm_sqrt_q15(q15_t in, q15_t * pOut)

    这里in的输入范围是0x0000 到 0x7FFF，转化成浮点数范围就是[0 +1)

10.4 实例讲解（Matlab验证）

实验目的：

    1. 学习FastMathFunctions中的Sine，Cosine和Sqrt，并配合Matlab进行验证结果

实验内容：

    1. 按下按键K1, 串口打印函数DSP_Cosine的输出结果

    2. 按下按键K2, 串口打印函数DSP_Sine的输出结果

    3. 按下按键K3, 串口打印函数DSP_Sqrt的输出结果

实验现象：

    通过窗口上位机软件SecureCRT（V5光盘里面有此软件）查看打印信息现象如下（以按下K1为例）：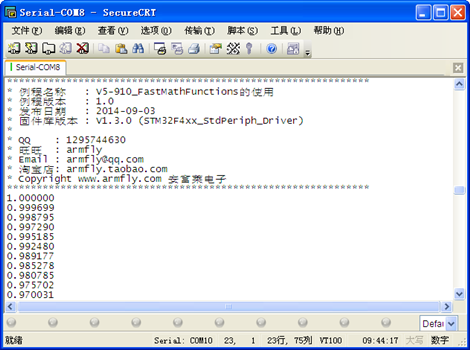

程序设计：

1. /*
   
2. *********************************************************************************************************
   : N: |9 M9 E( a& Z, h0 C9 ~
3. *        函 数 名: DSP_Cosine
   
4. *        功能说明: 求cos函数
   + t2 E. O3 ]' A; g5 G2 }
5. *        形    参：无
   
6. *        返 回 值: 无
   
7. *********************************************************************************************************
   4 h& k& k! A0 l
8. */
   
9. static void DSP_Cosine(void)
   
10. {
    
11. q31_t pOut;
    
12. float32_t pOut1;
    ! c! w( G  x5 k9 U/ G7 Z% B0 V
13. uint16_t i;
    
14. /***************************cos函数*****************************************/
    
15. for(i = 0; i < 256; i++)                                                                       (1)
    : @6 I! D, P" L) a' c# Z
16. {
    " o: E* e5 B0 t( j- J# c
17. /* 参数的输入范围是[0 2*pi) */
    & ]+ S6 E, h" u1 X2 j: L
18. printf("%f\r\n", arm_cos_f32(i * PI / 128));
    9 v) l* T3 n# n
19. }
    & {9 Z8 c: v4 i% d# ?' l
20. printf("***************************************************************\r\n");
    3 W: g. I% j; }: w1 q4 S8 X/ _3 G
21. for(i = 0; i < 256; i++)
    $ a9 D/ _5 n3 F# u7 Q! q  h7 j
22. {
    & h; f; f7 C$ p) l. F
23. /* 这里是0 到 32767 对于[0 2*pi) */
    + Y  g. T4 L+ b) [6 o
24. printf("%d\r\n", arm_cos_q15(i*128));
    
25. }
    
26. printf("***************************************************************\r\n");
    
27. for(i = 0; i < 256; i++)
    
28. {
    
29. /* 这里是0 到 2^31 - 1对应于[0 2*pi) */
    
30. printf("%d\r\n", arm_cos_q31(i*8388608));
    9 k+ S& K3 U' f- `7 i
31. }
    
32. printf("***************************************************************\r\n");
    
33. }
    4 d4 ]3 Z, M  X7 v6 y
34. 
    2 P+ D1 v+ d7 `4 \
35. /*
    
36. *********************************************************************************************************
    
37. *        函 数 名: DSP_Sine
    6 F$ U  G* K: V7 [7 L3 \
38. *        功能说明: 求sine函数
    9 ?( \; ]; ?- k/ ~6 W' c
39. *        形    参：无
    
40. *        返 回 值: 无
    / ?8 @! t5 O. y
41. *********************************************************************************************************
    ' V5 W& \1 A) E
42. */
    7 J# ~$ D( P8 D/ I  X  D
43. static void DSP_Sine(void)
    . B+ T! ~  L# M/ x! T+ Z0 J; S
44. {
    6 z8 p" x# E$ P. l9 k) v/ o% O2 O# f
45. q31_t pOut;
    & h$ X0 @/ P* M- R  F$ g# _
46. float32_t pOut1;
    
47. uint16_t i;
    9 ^; Z4 d* U0 y8 {# |9 v6 Q& \! M
48. /***************************sin函数*****************************************/
    - n% r$ P" z6 g, r( A9 s9 J4 k7 V
49. for(i = 0; i < 256; i++)                                                                        (2)
    
50. {
    
51. /* 参数的输入范围是[0 2*pi) */
    ' T0 X. U8 n* J1 B; y+ K8 |
52. printf("%f\r\n", arm_sin_f32(i * PI / 128));
    - g; }) o  v6 L, ~
53. }
    
54. printf("***************************************************************\r\n");
    ! h; q' O1 y" R
55. for(i = 0; i < 256; i++)
    
56. {
    
57. /* 这里是0 - 32767 对于[0 2*pi) */
    3 i+ W  F- n2 K/ V
58. printf("%d\r\n", arm_sin_q15(i*128));
    
59. }
    
60. printf("***************************************************************\r\n");
    
61. for(i = 0; i < 256; i++)
    2 Z5 m1 J- v/ `7 o' k0 e" ?! X/ N
62. {
    
63. /* 这里是0 - (pow(2, 31) - 1)对应于[0 2*pi) */
    
64. printf("%d\r\n", arm_sin_q31(i*8388608));
    
65. }
    8 ^  ]) b; c5 A
66. printf("***************************************************************\r\n");
    
67. }
    5 ^! C% S$ N) B
68. 
    
69. /*
    
70. *********************************************************************************************************
    : \; F2 [7 l# @9 P
71. *        函 数 名: DSP_Sqrt
    
72. *        功能说明: 求平方根
    
73. *        形    参：无
    1 j" ?" J$ u1 Y+ @3 f2 z; d
74. *        返 回 值: 无
    - J4 c$ }' l6 t9 q# d- w. j: N
75. *********************************************************************************************************
    ; e5 s% ?+ U# O# Z1 c* r+ ^
76. */
    $ ?: h* S/ P0 s' |- [
77. static void DSP_Sqrt(void)
    
78. {
    
79. q31_t pOut;
    
80. float32_t pOut1;
    
81. /* 求平方根 */
    8 I: d8 x% r  }( N$ B* v  D) k8 }0 v
82. arm_sqrt_q31(1000, &pOut);                                                                     (3)
    0 d4 t. Y2 ^' \$ l, z
83. printf("Value = %d\r\n", pOut);
    
84. arm_sqrt_f32(1000, &pOut1);
    8 t' l3 P2 I+ V3 `! u: `
85. printf("Value = %f\r\n", pOut1);
    
86. }

复制代码

1. 这里我们采样了cos曲线一个周期中的256个点。为了验证结果是否正确，我们可以将这些数据保存到txt文档中，复制这256个数据即可，然后保存并关闭文档。通过matlab加载这个txt文档，加载方法如下：

    打开后出现如下界面，点击按钮Next >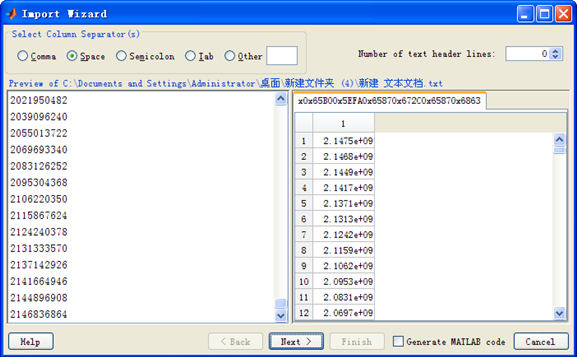

    出现如下界面后点击按钮Finish，即可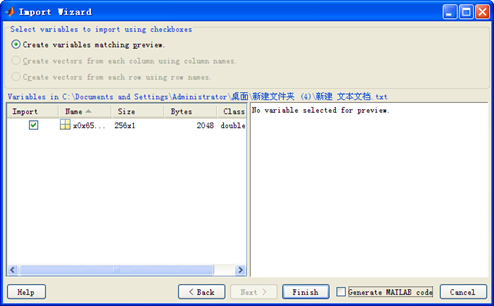

    然后再看工作区（Workspace）就能看到添加的数组变量了：

    现在我们通过matlab中的plot功能绘制下这些数据，绘制方法如下：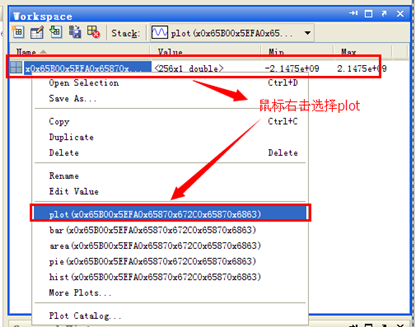

    绘制后的结果如下：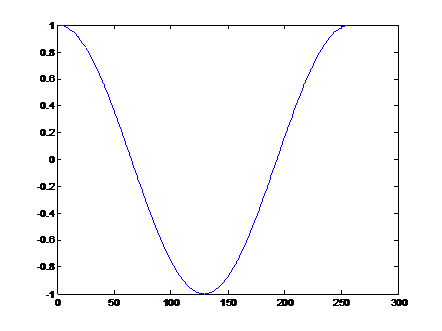

    从波形上看基本是一个周期的cos函数曲线。下面我们在把cos_q31和cos_q15函数分别绘制一下。

（这里要特别的注意Y轴，这个数值要除以2^31才是实际的cos数值）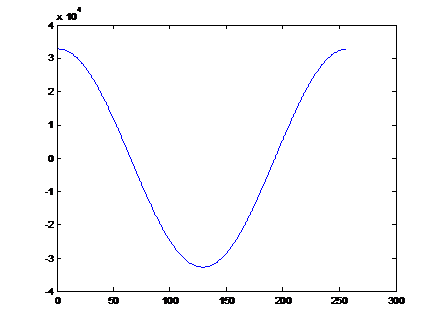

（这里要特别的注意Y轴，这个数值要除以2^15才是实际的cos数值）

2. sin和cos基本是一样的，这里就不再赘述了。

3. 平方根的含义在10.3.1已经详细讲解了。

10.5 总结

    本期教程就跟大家讲这么多，有兴趣的可以深入研究这些函数源码的实现。

8 B, m2 S8 y# K) |

谢谢分享啊

谢谢楼主咯

多谢楼主分享，收下了