特别说明：完整45期数字信号处理教程，原创高性能示波器代码全开源地址：链接
" S$ V, ]% t& h; N

第30章 复数FFT的实现

  m' m. `7 p( @" X$ m3 x

    本章主要讲解复数FFT的浮点和定点Q31，Q15的实现。

    本章节使用的复数FFT函数来自ARM官方库的TransformFunctions部分

     30.1 复数FFT

    30.2 复数FFT-基2算法

    30.3 复数FFT-基4算法

    30.4 总结

30.1 复数FFT30.1.1 描述

    当前复数FFT函数支持三种数据类型，分别是浮点，Q31和Q15。这些FFT函数有一个共同的特点，就是用于输入信号的缓冲，在转化结束后用来存储输出结果。这样做的好处是节省了RAM空间，不需要为输入和输出结果分别设置缓存。由于是复数FFT，所以输入和输出缓存要存储实部和虚部。存储顺序如下：{real[0], imag[0], real[1], imag[1],………………} ，在使用中切记不要搞错。

30.1.2 浮点

    浮点复数FFT使用了一个混合基数算法，通过多个基8与单个基2或基4算法实现。根据需要，该算法支持的长度[16，32，64，...，4096]和每个长度使用不同的旋转因子表。

    浮点复数FFT使用了标准的FFT定义，FFT正变换的输出结果会被放大fftLen倍数，计算FFT逆变换的时候会缩小到1/fftLen。这样就与教科书中的定义一致了。

    定义好的旋转因子和位反转表已经在头文件arm_const_structs.h中定义好了，调用浮点FFT函数arm_cfft_f32时，包含相应的头文件即可。比如：

       arm_cfft_f32(arm_cfft_sR_f32_len64, pSrc, 1, 1)

    上式就是计算一个64点的FFT逆变换包括位反转。数据结构arm_cfft_sR_f32_len64可以认为是常数，计算的过程中是不能修改的。同样是这种数据结构还能用于混合基的FFT正变换和逆变换。

    早期发布的浮点复数FFT函数版本包含基2和基4两种方法实现的，但是不推荐大家再使用了。现在全部用arm_cfft_f32代替了。

30.1.3 定点Q31和Q15

    定点库提供了基2和基4两种算法，基2算法支持的数据长度[16, 32, 64, ..., 4096]，基4算法支持的数据长度[16, 32, 64, ..., 4096]。一般情况下，建议使用基4算法，基4算法比基2算法执行速度要快一些。

    为了防止计算结果溢出，定点FFT每个蝶形运算的结果都要做放缩处理。对于基2算法，每次蝶形运算的结果要做0.5倍的放缩。对于基4算法，每次蝶形运算的结果要做0.25倍的放缩。FFT逆变换也要做相同的处理。相对于标准教科书式的FFT定义，定点FFT的计算结果放缩了1/fftLen（数据）倍。定点FFT的逆变也要做放缩处理，但是跟教科书式的FFT定义是相符的。

    每个FFT变换都需要一个单独的结构体，但结构体中的旋转因子和位反转表可以被重新使用。

    每个数据类型都有一个相关的初始化函数，初始化函数主要完成如下操作：

l 初始化结构体成员。

l 初始化旋转因子和位反转表指针。

    使用初始化函数是可选的。尽管如此，如果使用了初始化函数，那么结构体不能放在const data段，如果要放在const data段，应当按照如下方法进行初始化：

*arm_cfft_radix2_instance_q31 S = {fftLen, ifftFlag, bitReverseFlag, pTwiddle, pBitRevTable, twidCoefModifier, bitRevFactor};   

*arm_cfft_radix2_instance_q15 S = {fftLen, ifftFlag, bitReverseFlag, pTwiddle, pBitRevTable, twidCoefModifier, bitRevFactor};   

*arm_cfft_radix4_instance_q31 S = {fftLen, ifftFlag, bitReverseFlag, pTwiddle, pBitRevTable, twidCoefModifier, bitRevFactor};   

*arm_cfft_radix4_instance_q15 S = {fftLen, ifftFlag, bitReverseFlag, pTwiddle, pBitRevTable, twidCoefModifier, bitRevFactor};   

*arm_cfft_instance_f32 S = {fftLen, pTwiddle, pBitRevTable, bitRevLength};

    Q15和Q31 FFT使用了一个比较大的旋转因数和位反转表。这个表定义了一个最大长度的变换，表的子集可以用于短的变化。

30.1.4 arm_cfft_f32

函数定义如下：

    void arm_cfft_f32(

         const arm_cfft_instance_f32 * S,

         float32_t * p1,

         uint8_t ifftFlag,

         uint8_t bitReverseFlag)

参数定义：

     [in]   *S    points to an instance of the floating-point CFFT structure.  

     [in, out] *p1   points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.  

     [in] ifftFlag         flag that selects forward (ifftFlag=0) or inverse (ifftFlag=1) transform.  

     [in] bitReverseFlag  flag that enables (bitReverseFlag=1) or disables (bitReverseFlag=0) bit reversal of output.  

注意事项：

结构const arm_cfft_instance_f32的定义如下（在文件arm_math.h文件）：

      typedef struct

      {

          uint16_t fftLen;                  

          const float32_t *pTwiddle;         

          const uint16_t *pBitRevTable;      

          uint16_t bitRevLength;            

      } arm_cfft_instance_f32;

9 z% h0 `6 z* h6 a

    下面通过在开发板上运行这个函数并计算幅频相应，然后再与Matlab计算的结果做对比。

1. #define TEST_LENGTH_SAMPLES 2048
   7 h* F; h  E; S7 N) D
2. 
   
3. /* 输入和输出缓冲 */
   
4. static float32_t testOutput[TEST_LENGTH_SAMPLES/2];
     B+ \/ L3 Y  ?# G' j. [
5. static float32_t testInput_f32_10khz[TEST_LENGTH_SAMPLES];
   2 P7 e4 |4 s* Q2 X
6. 
   
7. /* 变量 */
   
8. uint32_t fftSize = 1024;
   
9. uint32_t ifftFlag = 0;
   
10. uint32_t doBitReverse = 1;
    . h, b: d, x/ T# s: X. R7 ~
11. 
    
12. /*
    
13. *********************************************************************************************************
    
14. *        函 数 名: arm_cfft_f32_app
    0 U) G% _, J$ k0 c
15. *        功能说明: 调用函数arm_cfft_f32_app计算幅频。
    
16. *        形    参：无
      u; N, T( P+ G# }
17. *        返 回 值: 无
    
18. *********************************************************************************************************
    4 Q' C2 a- p# I- C
19. */
    ! \. j9 L2 L: |: \0 ]& x2 \
20. void arm_cfft_f32_app(void)
    
21. {
    
22. uint16_t i;
    # T4 H* `3 e/ Z/ {( V( {' I
23. /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    ! ]. W% o9 t5 E  Y& l
24. for(i=0; i<1024; i++)
    
25. {
    1 D2 f6 L: a& c% D, \. U  k0 {6 T4 _
26. /* 虚部全部置零 */
    
27. testInput_f32_10khz[i*2+1] = 0;
    . n8 d( Z8 x/ x5 I+ _/ T9 _
28. /* 50Hz正弦波，采样率1KHz ,作为实部 */
    
29. testInput_f32_10khz[i*2] = arm_sin_f32(2*3.1415926f*50*i/1000);
    
30. }
    
31. /* CFFT变换 */
    + |$ `+ {5 f" [( P# P7 X" \
32. arm_cfft_f32(&arm_cfft_sR_f32_len1024, testInput_f32_10khz, ifftFlag, doBitReverse);
    
33. 
    ) w3 _* F# M( L9 d3 E$ a
34. /* 求解模值  */
    0 I" N) U, m, v1 |( |
35. arm_cmplx_mag_f32(testInput_f32_10khz, testOutput, fftSize);
    2 a# s9 g  U8 y3 m! y/ Z* G
36. /* 串口打印求解的模值 */
    - j( `. g0 q1 K3 |4 [
37. for(i=0; i<1024; i++)
    
38. {
    
39. printf("%f\r\n", testOutput[i]);
    
40. }
    
41. 
    7 F2 X$ ?1 \3 t( e  O
42. }

复制代码

运行如上函数可以通过串口打印出计算的模值，下面我们就通过Matlab计算的模值跟arm_cfft_f32计算的模值做对比。

    对比前需要先将串口打印出的数据加载到Matlab中，并给这个数组起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

Fs = 1000;                % 采样率

N  = 1024;               % 采样点数

n  = 0:N-1;               % 采样序列

t  = 0:1/Fs:1-1/Fs;        % 时间序列

f = n * Fs / N;             %真实的频率

. X# t6 R' P2 f9 I1 m) h
, J3 w& r/ B3 D' R8 |  `7 `

x = sin(2*pi*50*t) ;  %原始信号

y = fft(x, N);        %对原始信号做FFT变换

% I5 }% Y- k1 a& G
1 q3 j6 P; c9 G( W7 q% F

subplot(2,1,2);

plot(f, abs(y));       %绘制幅频相应曲线

title('Matlab计算结果');

xlabel('频率');

ylabel('幅度');

5 E. Y0 I! U5 g2 \# K$ Z, G

subplot(2,1,1);

plot(f,  sampledata);       %绘制幅频相应曲线

title('复数FFT计算结果');

xlabel('频率');

ylabel('幅度');

* m1 @& v9 C$ ?* f5 a3 q

Matlab运行结果如下：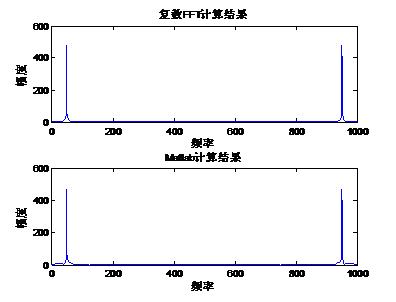

从上面的对比结果中可以看出，Matlab和函数arm_cfft_f32计算的结果基本是一直的。

1 U) @9 P- \) I5 c. \

30.2 复数FFT—基2算法
30.2.1 arm_cfft_radix2_f32

    此函数已经不推荐使用，后面的版本会被删除，故不做介绍。

30.2.2 arm_cfft_radix2_q31

函数定义如下：

    void arm_cfft_radix2_q31(

    const arm_cfft_radix2_instance_q31 * S,

    q31_t * pSrc)

参数定义：

    [in]      *S    points to an instance of the fixed-point CFFT/CIFFT structure.  

    [in, out] *pSrc  points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.

注意事项：

结构const  arm_cfft_radix2_instance_q31的定义如下（在文件arm_math.h文件）：

      typedef struct

      {

          uint16_t fftLen;               

          uint8_t ifftFlag;               

          uint8_t bitReverseFlag;         

          q31_t *pTwiddle;                 

          uint16_t *pBitRevTable;         

          uint16_t twidCoefModifier;      

          uint16_t bitRevFactor;         

      } arm_cfft_radix2_instance_q31;

7 {+ j, X* E& q4 V& s

    下面通过在开发板上运行这个函数并计算幅频相应，然后再与Matlab计算的结果做对比。

1. q31_t testInput_radix2_q31_50hz[TEST_LENGTH_SAMPLES];
   
2. q31_t testOutputQ31[TEST_LENGTH_SAMPLES/2];
   
3. 
   
4. /*
   ; r7 H1 E0 S5 T. a
5. *********************************************************************************************************
   
6. *        函 数 名: arm_cfft_radix2_q31_app
   . J; ~5 u# R  ], ^4 Z
7. *        功能说明: 调用函数arm_cfft_radix2_q31计算幅频。
   
8. *        形    参：无
   ! d8 R: h4 Q& I" r0 y( |
9. *        返 回 值: 无
   . \  O8 p/ m& m
10. *********************************************************************************************************
    
11. */
    & {1 [& C, I, h- Q7 x" |9 u0 P- {
12. void arm_cfft_radix2_q31_app(void)
    
13. {
    
14. uint16_t i,j;
    
15. arm_cfft_radix2_instance_q31 S;
    
16. fftSize = 1024;
    $ ^; C* X2 k8 T( i$ i9 ~
17.     ifftFlag = 0;
    
18.     doBitReverse = 1;
      P) }3 q* L. f6 J) W2 k
19. /* 初始化结构S */
    0 w0 G; o0 i" ]1 G7 |, I% H) u/ c
20. arm_cfft_radix2_init_q31(&S, fftSize, ifftFlag, doBitReverse);
    9 q6 _: k& I  j
21. /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    " T0 j8 k0 N/ `& I1 @( K
22. for(i=0; i<1024; i++)
    0 G$ Y1 X6 q& J. J+ t
23. {
    & e# D* n6 D7 v8 u
24. testInput_radix2_q31_50hz[i*2+1] = 0;
    ! B. @, f/ N1 ]3 N
25. /* 51.2Hz正弦波，采样率1024Hz。
    . C( E, \7 R3 q" B- F
26.    arm_sin_q31输入参数的范围0-2^31， 这里每20次为一个完整的正弦波，
    
27.    2^31 / 20 = 107374182.4
    ( B, k! Q$ a# _, Z* y3 T& {# L( Q9 a
28. */
    
29. j = i % 20;
    
30.           testInput_radix2_q31_50hz[i*2] = arm_sin_q31(107374182*j);
    
31.           printf("%d\r\n", testInput_radix2_q31_50hz[i*2]);
    
32. }
    " O; X2 V( n. I' V# z
33. /* 输出结果分割线 */
    
34. printf("**************************************************\r\n");
    : y1 p% \* [& q( ?
35. printf("**************************************************\r\n");
    
36. /* 计算CFFT */
    8 O4 e% m) R; D
37. arm_cfft_radix2_q31(&S, testInput_radix2_q31_50hz);
    / R/ n7 e6 D/ ^" }- @
38. /* 计算模值 */
    
39. arm_cmplx_mag_q31(testInput_radix2_q31_50hz, testOutputQ31, fftSize);
    4 X; l1 N# u2 D* S  d* T4 t7 d
40. /* 串口打印求解的模值 */
    
41. for(i=0; i<1024; i++)
    
42. {
    
43. printf("%d\r\n", testOutputQ31[i]);
    
44. }
    
45. }

复制代码

运行如上函数可以通过串口打印出原始信号和计算的模值，下面我们就通过Matlab计算的模值跟arm_cfft_radix2_q31计算的模值做对比。

    对比前需要先将串口打印出的数据加载到Matlab中，原始信号起名signal，函数arm_cmplx_mag_q31计算的模值起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

Fs = 1024;              % 采样率

N  = 1024;             % 采样点数

n  = 0:N-1;             % 采样序列

f = n * Fs / N;           %真实的频率

) L' r1 p' u+ n$ ?
% k! ?: X* M( F6 b. Q3 s

y = fft(signal, N);        %对原始信号做FFT变换

2 o2 v# z5 e/ \8 o- ^2 @& W6 V

subplot(2,1,2);

plot(f, abs(y));           %绘制幅频相应曲线

title('Matlab计算结果');

xlabel('频率');

ylabel('幅度');

1 {) R8 t3 W# l  p& f5 ^

subplot(2,1,1);

plot(f,  sampledata);      %绘制幅频相应曲线

title('复数FFT计算结果');

xlabel('频率');

ylabel('幅度');

Matlab运行结果如下：

从上面的对比结果中可以看出，Matlab和函数arm_cfft_radix2_q31计算的频率点基本是一致的，而幅值大小不一样是因为调用函数arm_cmplx_mag_q31对数据结果做了移位处理。

30.2.3 arm_cfft_radix2_q15

函数定义：

    void arm_cfft_radix2_q15(

        const  arm_cfft_radix2_instance_q15 * S,

        q15_t  * pSrc)

参数定义：

    [in]      *S    points to an instance of the fixed-point CFFT/CIFFT structure.  

    [in, out] *pSrc  points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.  

注意事项：

结构const  arm_cfft_radix2_instance_q15的定义如下（在文件arm_math.h文件）：

      typedef struct

      {

         uint16_t fftLen;               

          uint8_t ifftFlag;               

          uint8_t bitReverseFlag;         

          q15_t *pTwiddle;                    

      uint16_t *pBitRevTable;         

      uint16_t twidCoefModifier;      

          uint16_t bitRevFactor;         

      } arm_cfft_radix2_instance_q15;

' h$ ^, B4 o( r% b: L, S# H

    下面通过在开发板上运行这个函数并计算幅频相应，然后再与Matlab计算的结果做对比。

1. q15_t testInput_radix2_q15_50hz[TEST_LENGTH_SAMPLES];
   1 p1 o0 n" ]+ E% Q
2. q15_t testOutputQ15[TEST_LENGTH_SAMPLES/2];
   + Y2 s; b4 W4 S4 `, t" ~
3. 
   
4. /*
   7 Q* c! K  {, v. [- K7 I: f2 ?6 `2 O
5. *********************************************************************************************************
   9 `/ T; c4 ~! d! l
6. *        函 数 名: arm_cfft_radix2_q15_app
   
7. *        功能说明: 调用函数arm_cfft_radix2_q15计算幅频。
   
8. *        形    参：无
   $ U! ]! N, M, n! c
9. *        返 回 值: 无
   
10. *********************************************************************************************************
    : \& Q2 x4 T. x# {7 ?( k
11. */
    " w5 v: q; o( B7 F* _
12. void arm_cfft_radix2_q15_app(void)
    
13. {
    % y/ o) o$ r. W" V+ c7 v3 Z* {  n
14. uint16_t i,j;
    # S; Q3 G/ a+ V8 F4 w! C
15. arm_cfft_radix2_instance_q15 S;
    
16. fftSize = 1024;
    
17.     ifftFlag = 0;
    # _+ D5 G! U1 }) ?. y
18.     doBitReverse = 1;
    ( M+ y+ Y; P# `; S7 p! Y' }! P
19. /* 初始化结构S */
    
20. arm_cfft_radix2_init_q15(&S, fftSize, ifftFlag, doBitReverse);
    0 i, a' u4 G! I, Y/ c1 j$ w
21. /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    / D' `" }& B9 _, k! q3 b4 Q
22. for(i=0; i<1024; i++)
    
23. {
      l) U) f+ x! j0 G3 t" Y+ U5 d
24. /* 虚部全部置0 */
    3 Q0 A3 Z& k9 }2 ^& K5 c% l: p& z
25. testInput_radix2_q15_50hz[i*2+1] = 0;
    
26. /* 51.2Hz正弦波，采样率1024Hz。
    
27.    arm_sin_q15输入参数的范围[0, 32768)， 这里每20次为一个完整的正弦波，
    
28.    32768 / 20 = 1638.4
    
29. */
    
30. j = i % 20;
    
31.           testInput_radix2_q15_50hz[i*2] = arm_sin_q15(1638*j);
    
32.           printf("%d\r\n", testInput_radix2_q15_50hz[i*2]);
    / a+ O9 j$ d) N$ S  E& i7 q) h
33. }
    
34. /* 输出结果分割线 */
    
35. printf("**************************************************\r\n");
    / v) v2 t5 q# O, g/ u
36. printf("**************************************************\r\n");
    ! v$ ?7 e7 x$ W0 E7 S9 Z0 X
37. /* 计算CFFT */
    6 ^+ q* k& s$ F0 i
38. arm_cfft_radix2_q15(&S, testInput_radix2_q15_50hz);
    
39. /* 计算模值 */
    
40. arm_cmplx_mag_q15(testInput_radix2_q15_50hz, testOutputQ15, fftSize);
    
41. /* 串口打印求解的模值 */
    
42. for(i=0; i<1024; i++)
    9 x! n8 A; K- s: I$ I& J6 Z
43. {
    
44. printf("%d\r\n", testOutputQ15[i]);
    
45. }
    6 X4 y) A2 ?$ a$ C! D' D5 n
46. }

复制代码

运行如上函数可以通过串口打印出原始信号和计算的模值，下面我们就通过Matlab计算的模值跟arm_cfft_radix2_q15计算的模值做对比。

    对比前需要先将串口打印出的数据加载到Matlab中，原始信号起名signal，函数arm_cmplx_mag_q15计算的模值起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

Fs = 1024;                     % 采样率

N  = 1024;                     % 采样点数

n  = 0:N-1;                     % 采样序列

f = n * Fs / N;                %真实的频率

" P6 G( z* @' I

y = fft(signal, N);           %对原始信号做FFT变换

subplot(2,1,2);

plot(f, abs(y));           %绘制幅频相应曲线

title('Matlab计算结果');

xlabel('频率');

ylabel('幅度');

# B9 M4 K" s, E8 i& ~

subplot(2,1,1);

plot(f,  sampledata);      %绘制幅频相应曲线

title('复数FFT计算结果');

xlabel('频率');

ylabel('幅度');

Matlab运行结果如下：

从上面的对比结果中可以看出，Matlab和函数arm_cfft_radix2_q15计算的频率点基本是一致的，而幅值大小不一样是因为调用函数arm_cmplx_mag_q15对数据结果做了移位处理。

/ C# }# t( u/ c" i1 d3 z9 q

30.3 复数FFT—基4算法

    如果希望直接调用FFT程序计算IFFT，可以用下面的方法：

30.3.1 arm_cfft_radix4_f32

    此函数已经不推荐使用，后面的版本会被删除，故不做介绍。

30.3.2 arm_cfft_radix4_q31

函数定义如下：

    void arm_cfft_radix4_q31(

    const arm_cfft_radix4_instance_q31 * S,

    q31_t * pSrc)

参数定义：

    [in]      *S    points to an instance of the fixed-point CFFT/CIFFT structure.  

    [in, out] *pSrc  points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.

注意事项：

1. 结构const  arm_cfft_radix4_instance_q31的定义如下（在文件arm_math.h文件）：

      typedef struct

      {

          uint16_t fftLen;               

          uint8_t ifftFlag;               

          uint8_t bitReverseFlag;         

          q31_t *pTwiddle;                 

          uint16_t *pBitRevTable;         

          uint16_t twidCoefModifier;      

          uint16_t bitRevFactor;         

       } arm_cfft_radix4_instance_q31;

2. 为了防止数据饱和，每次蝶形运行的结果都要除以2，故不同的长度的FFT运算的最终结果输出格式不同。具体信息如下：

    Q31 CFFT

    Q31 CIFFT

    下面通过在开发板上运行这个函数并计算幅频相应，然后再与Matlab计算的结果做对比。

1. q31_t testInput_radix4_q31_50hz[TEST_LENGTH_SAMPLES];
   , {) a' l3 F+ t- e2 v* D
2. /*
   # W+ T9 [4 B' H/ u, ~3 W
3. *********************************************************************************************************
   
4. *        函 数 名: arm_cfft_radix4_q31_app
   
5. *        功能说明: 调用函数arm_cfft_radix4_q31_app计算幅频。
   
6. *        形    参：无
   
7. *        返 回 值: 无
   
8. *********************************************************************************************************
   
9. */
   
10. void arm_cfft_radix4_q31_app(void)
    - z1 D# G: f5 O& A: h0 b
11. {
    
12. uint16_t i,j;
    
13. arm_cfft_radix4_instance_q31 S;
    5 F, E: {3 P6 q( y2 h6 O2 x$ P
14. fftSize = 1024;
    
15.     ifftFlag = 0;
    
16.     doBitReverse = 1;
    
17. /* 初始化结构S */
    
18. arm_cfft_radix4_init_q31(&S, fftSize, ifftFlag, doBitReverse);
    
19. /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    
20. for(i=0; i<1024; i++)
    ! U. m' \$ g& O0 G9 C
21. {
    5 p" J/ J, O0 n) e  M7 m
22. testInput_radix4_q31_50hz[i*2+1] = 0;
    
23. /* 51.2Hz正弦波，采样率1024Hz。
    
24.    arm_sin_q31输入参数的范围0-2^31， 这里每20次为一个完整的正弦波，
    
25.    2^31 / 20 = 107374182.4
    
26. */
    " I) `+ K9 c9 n
27. j = i % 20;
    
28.           testInput_radix4_q31_50hz[i*2] = arm_sin_q31(107374182*j);
    
29.           printf("%d\r\n", testInput_radix4_q31_50hz[i*2]);
    
30. }
    . P" Q9 B+ _3 q- n8 a9 W  x, G! @- Y
31. /* 输出结果分割线 */
    
32. printf("**************************************************\r\n");
    ( C1 G: Y, i% {4 @4 P% d
33. printf("**************************************************\r\n");
    
34. /* 计算CFFT */
    . q' P$ C5 D( H- D
35. arm_cfft_radix4_q31(&S, testInput_radix4_q31_50hz);
    ' v5 t5 ]. Q- N/ l* q
36. /* 计算模值 */
    
37. arm_cmplx_mag_q31(testInput_radix4_q31_50hz, testOutputQ31, fftSize);
    
38. /* 串口打印求解的模值 */
    1 q! X! B! ?- X- K% W
39. for(i=0; i<1024; i++)
    
40. {
    
41. printf("%d\r\n", testOutputQ31[i]);
    
42. }
    + }- d4 V$ a8 J' }+ T  F
43. }

复制代码

运行如上函数可以通过串口打印出原始信号和计算的模值，下面我们就通过Matlab计算的模值跟arm_cfft_radix4_q31计算的模值做对比。

    对比前需要先将串口打印出的数据加载到Matlab中，原始信号起名signal，函数arm_cmplx_mag_q31计算的模值起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

Fs = 1024;              % 采样率

N  = 1024;             % 采样点数

n  = 0:N-1;             % 采样序列

f = n * Fs / N;           %真实的频率

# a7 B) x4 K" u5 ?4 t

y = fft(signal, N);        %对原始信号做FFT变换

( F- T7 w7 k+ ]# c2 t9 P

subplot(2,1,2);

plot(f, abs(y));           %绘制幅频相应曲线

title('Matlab计算结果');

xlabel('频率');

ylabel('幅度');

subplot(2,1,1);

plot(f,  sampledata);      %绘制幅频相应曲线

title('复数FFT计算结果');

xlabel('频率');

ylabel('幅度');

Matlab运行结果如下：

从上面的对比结果中可以看出，Matlb和函数arm_cfft_radix4_q31计算的频率点基本是一致的，而幅值大小不一样是因为调用函数arm_cmplx_mag_q31和arm_cfft_radix4_q31对数据结果做了移位处理。

' W2 v* N: l* [: x30.3.3 arm_cfft_radix4_q15

函数定义：

    void arm_cfft_radix4_q15(

        const  arm_cfft_radix4_instance_q15 * S,

        q15_t  * pSrc)

参数定义：

    [in]      *S    points to an instance of the fixed-point CFFT/CIFFT structure.  

    [in, out] *pSrc  points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.  

注意事项：

1. 结构const  arm_cfft_radix4_instance_q15的定义如下（在文件arm_math.h文件）：

      typedef struct

      {

          uint16_t fftLen;               

          uint8_t ifftFlag;               

          uint8_t bitReverseFlag;         

          q15_t *pTwiddle;                    

      uint16_t *pBitRevTable;         

      uint16_t twidCoefModifier;      

          uint16_t bitRevFactor;         

      } arm_cfft_radix4_instance_q15;

2. 为了防止数据饱和，每次蝶形运行的结果都要除以2，故不同的长度的FFT运算的最终结果输出格式不同。具体信息如下：

    Q15 CFFT

    Q15 CIFFT

    下面通过在开发板上运行这个函数并计算幅频相应，然后再与Matlab计算的结果做对比。

1. q15_t testInput_radix4_q15_50hz[TEST_LENGTH_SAMPLES];
   
2. /*
   & h1 q8 y. z) r' X
3. *********************************************************************************************************
   / n& q& I  Y2 e  W* r
4. *        函 数 名: arm_cfft_radix4_q15_app
   ( ^* K- D) B9 g6 J$ n" a
5. *        功能说明: 调用函数arm_cfft_radix4_q15计算幅频。
   5 R2 v7 O$ d" O2 h
6. *        形    参：无
   * _% G# j  t: q" q$ M  E. C
7. *        返 回 值: 无
   / t1 ^' d( M+ E+ J  O) z5 o
8. *********************************************************************************************************
   
9. */
   ! z7 o+ t4 l. N
10. void arm_cfft_radix4_q15_app(void)
    # r' n! P# {& h- F
11. {
    2 K$ b+ t5 _$ {' Q  u3 z9 I
12. uint16_t i,j;
    ! N% o+ F- e. o0 G0 D
13. arm_cfft_radix4_instance_q15 S;
    9 }/ l" {, A* w/ y  l$ G
14. fftSize = 1024;
    . H3 {9 X: [# |# M
15.     ifftFlag = 0;
    
16.     doBitReverse = 1;
    5 S' E9 L% j1 x7 Y+ c
17. /* 初始化结构S */
    
18. arm_cfft_radix4_init_q15(&S, fftSize, ifftFlag, doBitReverse);
    
19. /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    / h. \: b) v2 u* Y! |
20. for(i=0; i<1024; i++)
    * F- {- s3 J3 l& y& Y* |6 i5 }1 _
21. {
    ! T& C1 k- Q$ z, \6 x3 T# c
22. /* 虚部全部置0 */
    
23. testInput_radix4_q15_50hz[i*2+1] = 0;
    
24. /* 51.2Hz正弦波，采样率1024Hz。
    7 Z6 m( t' Q+ w  u
25.    arm_sin_q15输入参数的范围[0, 32768)， 这里每20次为一个完整的正弦波，
    
26.    32768 / 20 = 1638.4
    
27. */
    
28. j = i % 20;
      L; D( C. W% W7 V( f
29.           testInput_radix4_q15_50hz[i*2] = arm_sin_q15(1638*j);
    
30.           printf("%d\r\n", testInput_radix4_q15_50hz[i*2]);
    
31. }
    
32. /* 输出结果分割线 */
    
33. printf("**************************************************\r\n");
    
34. printf("**************************************************\r\n");
      l, H. L7 y* l4 J" C
35. /* 计算CFFT */
    
36. arm_cfft_radix4_q15(&S, testInput_radix4_q15_50hz);
    
37. /* 计算模值 */
      A4 d& b" a) Y2 i
38. arm_cmplx_mag_q15(testInput_radix4_q15_50hz, testOutputQ15, fftSize);
    
39. /* 串口打印求解的模值 */
    
40. for(i=0; i<1024; i++)
    / O: h# ?3 t4 M
41. {
    8 B5 m( L+ B- A* r
42. printf("%d\r\n", testOutputQ15[i]);
    2 W& |, L. {' X5 |+ k% L
43. }
    / X2 k9 ^. Y0 T5 t/ C% W& k$ l2 b
44. }

复制代码

运行如上函数可以通过串口打印出原始信号和计算的模值，下面我们就通过Matlab计算的模值跟arm_cfft_radix4_q15计算的模值做对比。

    对比前需要先将串口打印出的数据加载到Matlab中，原始信号起名signal，函数arm_cmplx_mag_q15计算的模值起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

Fs = 1024;                     % 采样率

N  = 1024;                     % 采样点数

n  = 0:N-1;                     % 采样序列

f = n * Fs / N;                %真实的频率

y = fft(signal, N);           %对原始信号做FFT变换

: P/ K; p& L# e/ g/ T! k
; g3 P6 C5 H2 e1 f

subplot(2,1,2);

plot(f, abs(y));           %绘制幅频相应曲线

title('Matlab计算结果');

xlabel('频率');

ylabel('幅度');

. Y5 d6 E* j' w% y

subplot(2,1,1);

plot(f,  sampledata);      %绘制幅频相应曲线

title('复数FFT计算结果');

xlabel('频率');

ylabel('幅度');

) l- L. D" ?0 ?% V5 j4 K2 d/ ~

Matlab运行结果如下：

从上面的对比结果中可以看出，Matlab和函数arm_cfft_radix4_q15计算的频率点基本是一致的，而幅值大小不一样是因为调用函数arm_cmplx_mag_q15和arm_cfft_radix4_q15对数据结果做了移位处理。

$ f: d, V- V8 ^4 w( w: z4 ~" U

30.4 总结

    本章节内容比较多，有兴趣的可以深入了解源码的实现。

0 L9 s3 T+ x8 V& D) x

标记下学习

mark一下！