特别说明：完整45期数字信号处理教程，原创高性能示波器代码全开源地址：链接

第31章 复数FFT的逆变换实现

    本章主要讲解复数FFT的逆变换。

    本章节使用的复数FFT函数来自ARM官方库的TransformFunctions部分

    31.1 复数FFT 的逆变换实现

    31.2 总结

31.1 复数FFT的逆变换实现

    本小节主要讲解复数FFT的逆变换实现，通过函数arm_cfft_f32实现浮点数的逆变换。

31.1.1 arm_cfft_f32逆变换

函数定义如下：

    void arm_cfft_f32(

         const arm_cfft_instance_f32 * S,

         float32_t * p1,

         uint8_t ifftFlag,

         uint8_t bitReverseFlag)

参数定义：

     [in]   *S    points to an instance of the floating-point CFFT structure.  

     [in, out] *p1   points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.  

     [in] ifftFlag         flag that selects forward (ifftFlag=0) or inverse (ifftFlag=1) transform.  

     [in] bitReverseFlag  flag that enables (bitReverseFlag=1) or disables (bitReverseFlag=0) bit reversal of output.  

注意事项：

结构const arm_cfft_instance_f32的定义如下（在文件arm_math.h文件）：

      typedef struct

      {

          uint16_t fftLen;                  

          const float32_t *pTwiddle;         

          const uint16_t *pBitRevTable;      

          uint16_t bitRevLength;            

      } arm_cfft_instance_f32;

    下面通过函数arm_cfft_f32计算一个正弦波的FFT，然后再使用函数arm_cfft_f32做FFT逆变换，并使用 Matlab计算变换前后的结果对比。

1. /*
   
2. *********************************************************************************************************
   
3. *        函 数 名: arm_cfft_f32_app
   
4. *        功能说明: 调用函数arm_cfft_f32_app计算CFFT正变换和你变换。
   
5. *        形    参：无
   
6. *        返 回 值: 无
   
7. *********************************************************************************************************
   
8. */
   
9. static void arm_cfft_f32_app(void)
   
10. {
    
11. uint16_t i;
    
12. fftSize = 1024;
    
13.     ifftFlag = 0;
    
14.     doBitReverse = 1;
    
15. /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    
16. for(i=0; i<1024; i++)
    
17. {
    
18. testInput_f32_10khz[i*2+1] = 0;
    
19. /* 50Hz正弦波，采样率1KHz */
    
20. testInput_f32_10khz[i*2] = arm_sin_f32(2*3.1415926f*50*i/1000);
    
21. printf("%f\r\n", testInput_f32_10khz[i*2]);
    
22. }
    
23. /* CFFT变换：FFT正变换 */
    
24. arm_cfft_f32(&arm_cfft_sR_f32_len1024, testInput_f32_10khz, ifftFlag, doBitReverse);
    
25. 
    
26. ifftFlag = 1;
    
27. /* CFFT变换：FFT逆变换 */
    
28. arm_cfft_f32(&arm_cfft_sR_f32_len1024, testInput_f32_10khz, ifftFlag, doBitReverse);
    
29. 
    
30. printf("****************************分割线***************************************\r\n");
    
31. /* 串口打印求解的模值 */
    
32. for(i=0; i<1024; i++)
    
33. {
    
34. printf("%f\r\n", testInput_f32_10khz[i*2]);
    
35. }
    
36. 
    
37. }

复制代码

运行如上函数可以通过串口打印出原始正弦波和经过CFFT，CIFFT的正弦波，下面我们就通过Matlab对比变换前和变换后的波形。

    对比前需要先将串口打印出的两组数据加载到Matlab中，并给原始正弦波起名signal，变换后的数组起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

Fs = 1000;                     % 采样率

N  = 1024;                     % 采样点数

n  = 0:N-1;                     % 采样序列

f = n * Fs / N;                 %真实的频率

subplot(2,1,1);

plot(f,  signal);      %绘制原始信号

title('原始信号');

xlabel('时间');

ylabel('幅值');

subplot(2,1,2);

plot(f,  sampledata);    %绘制CFFT和CIFFT后的信号

title('CFFT和CIFFT后的信号');

xlabel('时间');

ylabel('幅值');

Matlab运行的结果如下：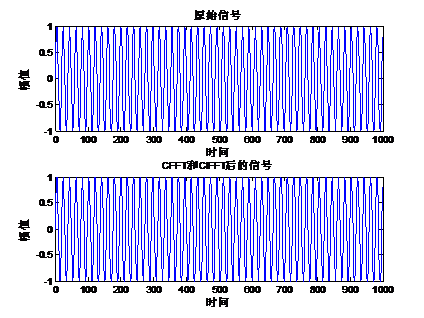

波形前端部分：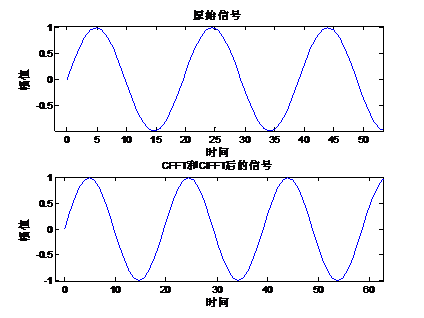

波形后端部分：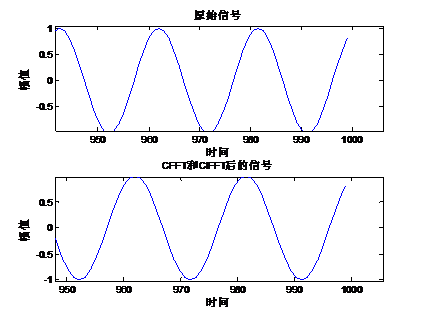

从上面的对比结果中可以看出，函数arm_cfft_f32计算前后的正弦波基本是一致的。

31.2 总结

     本章节内容较少，主要验证了函数arm_cfft_f32正变换和逆变换，有兴趣的可以验证Q31和Q15两种数据类型的正变换和逆变换。

沙发，赞一个

主要是没得F4的板子，不然我也搞一搞这个