你的浏览器版本过低，可能导致网站不能正常访问！
为了你能正常使用网站功能，请使用这些浏览器。

st-img
chrome st-img
firefox st-img
safari st-img
ie8及以上

【原创】【安富莱——DSP教程】第39章 IIR滤波器的Matlab设计

[复制链接]
baiyongbin2009 发布时间：2015-4-27 10:48
特别说明：完整45期数字信号处理教程，原创高性能示波器代码全开源地址：链接
第39章 IIR滤波器的Matlab设计

    本章节讲解IIR滤波器的Matlab设计，主要包括巴特沃斯滤波器，切比雪夫I型和II型滤波器以及椭圆滤波器。
    39.1 巴特沃斯滤波器的设计
    39.2 切比雪夫滤波器的设计
    39.3 椭圆滤波器的设计
    39.4 总结

39.1 巴特沃斯滤波器的设计
39.1.1 butter函数
功能：用于设计Butterworth（巴特沃斯）滤波器
语法：[b, a] = butter(n, Wn);
说明：butter函数可以设计低通、带通、高通和带阻数字滤波器，其特性可以使通带内的幅度响应最大限度地平坦，但会损失截止频率处的下降斜度，使幅度响应衰减较慢。
l [b,a] = butter(n,Wn)可以设计截止频率为Wn的n阶低通butterworth滤波器，其中截止频率Wn应满足0Wn1，Wn=1相当于0.5fs（采样频率）。当Wn = [W1 W2]时，butter函数产生一个2n阶的数字带通滤波器，其通带为W1 < W < W2。
l [b,a] = butter(n,Wn,'ftype')可以设计高通或带阻滤波器。当ftype=high时，可设计截止频率为Wn的高通滤波器；当ftype=stop时，可设计带阻滤波器，此时Wn = [W1 W2]，阻带为W1 < W < W2。
    使用butter函数设计滤波器，可以使通带内的幅度响应最大地平坦，但会损失截止频率处的下降斜度。因此，butter函数主要用于设计通带平坦的数字滤波器。

39.1.2 buttord函数
功能：用来选择Butterworth滤波器的阶数。
语法：[n, Wn] = buttord（WP, WS, RP, Rs）；
说明：buttord函数可以在给定滤波器性能的情况下，选择Butterworth数字滤波器的最小阶数，其中WP和WS分别是通带和阻带的截止频率，其值为0Wp（或Ws）1，当该值为1时表示0.5fs（采样率）。RP和 Rs分别是通带和阻带区的波纹系数和衰减系数。
    [n, Wn] = buttord（WP, WS, RP, Rs）可以得到高通、带通和带阻滤波器的最小阶数n。
    当WP>WS时，为高通滤波器；当WP, WS为二元矢量时，若WP<WS，则为带通和带阻滤波器，此时Wn也为二元矢量。
    利用buttord函数可得到Butterworth数字滤波器的最小阶数n，并使通带（0，WP）内的波纹系数小于RP,阻带（WS, 1）内衰减系数大于Rs。buttord函数还可以得到截止频率Wn，再利用butter函数可产生满足指定性能的滤波器。
    使用butter函数设计数字滤波器，可以使通带内的幅度响应最大限度地平坦，但在截止频率附件幅度响应衰减慢。如果期望幅度响应下降斜度大，衰减快，可使用Elliptic(椭圆)或Chebyshev（切比雪夫）滤波器。

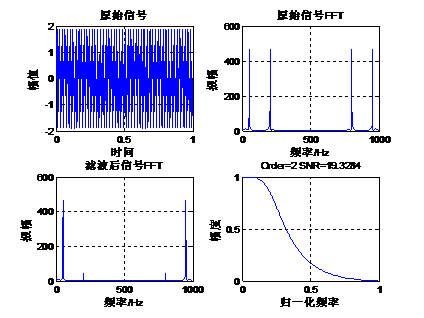
39.1.3 巴特沃斯低通滤波器设计
    下面我们通过一个实例来讲解巴特沃斯低通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将200Hz的正弦波当做噪声滤掉，下面通过函数butter设计一组低通滤波器系数，其阶数是2，截止频率为0.25（也就是125Hz），采样率1Kbps。Matlab运行代码如下：
  1. fs=1000;               %设置采样频率 1k
  2. N=1024;               %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;         %时间序列         
  5. f=n*fs/N;              %频率序列

  7. x1=sin(2*pi*50*t);      %信号
  8. x2=sin(2*pi*200*t);     %噪声
  9. x=x1+x2;               %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wc=2*125/fs;           %设置截止频率125Hz                 
  28. [b,a]=butter(2,Wc);   %获取2阶IIR滤波系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');        %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x1.^2);            %信号的总功率
  44. Pu=sum((y2-x1).^2);       %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);     %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
运算Malab结果如下：
39.1.png
从滤波的效果来看，2阶的IIR滤波器能够达到将近20的信噪比，比使用FIR需要更少的阶数。

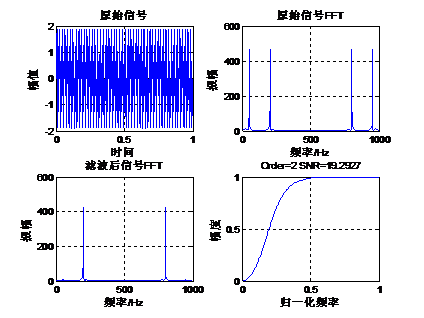
39.1.4 巴特沃斯高通滤波器设计
    下面我们通过一个实例来讲解巴特沃斯高通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将50Hz的正弦波当做噪声滤掉，下面通过函数butter设计一组高通滤波器系数，其阶数是2，截止频率为0.25（也就是125Hz），采样率1Kbps。Matlab运行代码如下：
  1. fs=1000;               %设置采样频率 1k
  2. N=1024;               %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;         %时间序列         
  5. f=n*fs/N;              %频率序列

  7. x1=sin(2*pi*50*t);      %噪声
  8. x2=sin(2*pi*200*t);     %信号
  9. x=x1+x2;              %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wc=2*125/fs;              %设置截止频率125Hz                 
  28. [b,a]=butter(2,Wc, 'high');   %获取2阶IIR滤波系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');       %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x2.^2);           %信号的总功率
  44. Pu=sum((y2-x2).^2);       %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);     %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Matlab运行结果如下：
39.2.png
从滤波的效果来看，2阶的IIR滤波器效果还是比较好的。

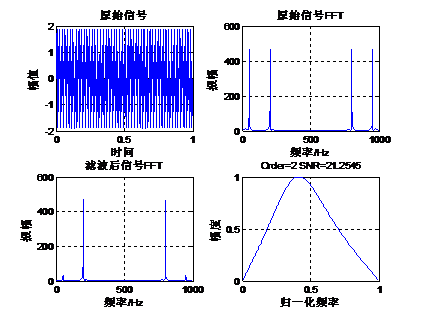
39.1.5 巴特沃斯带通滤波器设计
    下面我们通过一个实例来讲解巴特沃斯带通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将50Hz的正弦波当做噪声滤掉，下面通过函数butter设计一组带通滤波器系数，其阶数是2，通带为125Hz到300Hz，采样率1Kbps。Matlab运行代码如下：
  1. fs=1000;               %设置采样频率 1k
  2. N=1024;               %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;         %时间序列         
  5. f=n*fs/N;              %频率序列

  7. x1=sin(2*pi*50*t);      %噪声
  8. x2=sin(2*pi*200*t);     %信号
  9. x=x1+x2;              %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wn=[125*2 300*2]/fs;  %设置通带125Hz到300Hz                 
  28. [b,a]=butter(1,Wn);     %注意第一个参数虽然是1，但生成的却是2阶IIR滤波器系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');        %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x2.^2);            %信号的总功率
  44. Pu=sum((y2-x2).^2);        %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);   %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Matlab的计算结果如下：
39.3.png
从滤波的效果来看，2阶的IIR滤波器效果还是比较好的。

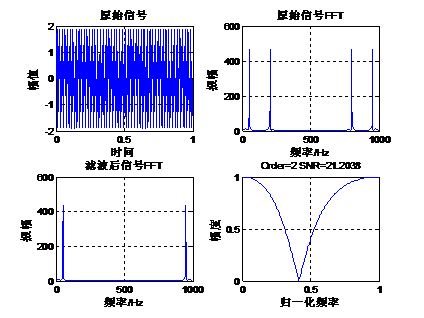
39.1.6 巴特沃斯带阻滤波器设计
    下面我们通过一个实例来讲解巴特沃斯带阻滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将200Hz的正弦波当做噪声滤掉，下面通过函数butter设计一组带阻滤波器系数，其阶数是2，阻带为125Hz到300Hz，采样率1Kbps。Matlab运行代码如下：
  1. fs=1000;              %设置采样频率 1k
  2. N=1024;              %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;        %时间序列         
  5. f=n*fs/N;             %频率序列

  7. x1=sin(2*pi*50*t);      %信号
  8. x2=sin(2*pi*200*t);     %噪声
  9. x=x1+x2;             %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wn=[125*2 300*2]/fs;       %设置阻带125Hz到300Hz                 
  28. [b,a]=butter(1,Wn, 'stop');   %注意第一个参数虽然是1，但生成的却是2阶IIR滤波器系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');        %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x1.^2);         %信号的总功率
  44. Pu=sum((y2-x1).^2);     %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);   %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Maltab运行结果如下：
39.4.png
从滤波的效果来看，2阶的IIR滤波器效果还是比较好的。

赞 收藏 1 评论6 发布时间：2015-4-27 10:48

举报

6个回答
baiyongbin2009 回答时间：2015-4-27 11:01:14
39.2 切比雪夫滤波器的设计
    切比雪夫（Chebyshev）滤波器分为Chebyshev I型和Chebyshev II型，分别具有通带等纹波和阻带等纹波性能。
39.2.1 cheby1函数
功能：用来设计Chebyshev（切比雪夫）I型滤波器（通带等纹波）。
语法：[b,a] = cheby1(n, Rp, Wn);
            [b,a] = cheby1(n, Rp, Wn, 'ftype');
说明：cheby1函数可以设计低通，带通，高通和带阻Chebyshev I型数字滤波器，其通带内为等纹波，阻带内为单调。Chebyshev I型滤波器的下降斜度比Chebyshev II型大，但其代价是在通带内纹波较大。
    [b,a] = cheby1(n, Rp, Wn);可以设计n阶低通Chebyshev I型数字滤波器，其中RP用来确定通带内的纹波，Wn为改滤波器的截止频率。
    当Wn=[W1, W2]时，cheby1函数可产生一个2n的数字带通滤波器，其通带为W1<W<W2。
    [b,a] = cheby1(n, Rp, Wn, 'ftype');可用来设计n阶高通或带阻滤波器，其中Rp和Wn同上，ftype的定义与butter相同。

39.2.2 cheby1ord函数
功能：用来选择Chebyshev I型滤波器的阶数。
语法：[n, Wn] = cheb1ord（WP, WS, RP, Rs）;
说明：cheb1ord函数可以在给定滤波器性能的情况下，选择Chebyshev I型数字滤波器的最小阶数，其中Wp和Ws分别是通带和阻带的截止频率，其值为0Wp（或Ws）1。Rp和Rs分别是通带和阻带区的波纹系数。
    [n, Wn] = cheb1ord（WP, WS, RP, Rs）;可以得到低通、高通、带通和带阻滤波器的最小阶数。
    利用cheblord函数，除了可以得到Chebyshev I型数字滤波器的最小阶数n外，还可以得到截止频率Wn，再利用cheby1函数可产生满足指定性能的滤波器，使滤波器通带(0, Wp)内的纹波系数小于Rp，阻带(WS, 1)内衰减系数大于RS

39.2.3 cheby2函数
功能：用来设计Chebyshev（切比雪夫）I型滤波器（通带等纹波）。
语法：[b,a] = cheby1(n, Rp, Wn);
            [b,a] = cheby1(n, Rp, Wn, 'ftype');
说明：cheby2函数与cheby1函数基本相同，只是用cheby2函数所设计的滤波器，其通带内为单调的，阻带内为等波纹，由RS指定阻带内的波纹。
    cheby2函数可以设计低通，带通，高通和带阻Chebyshev II型数字滤波器。

39.2.4 cheby2ord函数
功能：用来选择Chebyshev II型滤波器的阶数。
语法：[n, Wn] = cheb2ord（WP, WS, RP, Rs）;
说明：cheb2ord函数与cheb2函数类似，可以利用该函数确定Chebyshev II型数字滤波器的最小阶数n和截止频率Wn。
     cheb2ord函数和cheb2函数配合使用，可设计出最低阶数的Chebyshev II型数字滤波器。

39.2.5 切比雪夫I型低通滤波器设计
    下面我们通过一个实例来讲解切比雪夫I型低通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将200Hz的正弦波当做噪声滤掉，下面通过函数cheby1设计一组低通滤波器系数，其阶数是4，截止频率为0.25（也就是125Hz），采样率1Kbps，通带波纹1db。Matlab运行代码如下：
  1. fs=1000;               %设置采样频率 1k
  2. N=1024;               %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;         %时间序列         
  5. f=n*fs/N;              %频率序列

  7. x1=sin(2*pi*50*t);      %信号
  8. x2=sin(2*pi*200*t);     %噪声
  9. x=x1+x2;              %信号混合

  11. subplot(221);
  12. plot(t,x);                %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wc=2*125/fs;            %设置截止频率125Hz                 
  28. [b,a]=cheby1(4, 3, Wc);   %获取2阶IIR滤波系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);           %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');        %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x1.^2);            %信号的总功率
  44. Pu=sum((y2-x1).^2);       %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);     %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Matlab计算结果如下：
39.5.png
从滤波的效果来看，4阶的切比雪夫I型滤波效果还是比较好的。

39.2.6 切比雪夫I型高通滤波器设计
    下面我们通过一个实例来讲解切比雪夫I型高通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将50Hz的正弦波当做噪声滤掉，下面通过函数cheby1设计一组高通滤波器系数，其阶数是2，截止频率为0.25（也就是125Hz），采样率1Kbps，通带波纹1db。Matlab运行代码如下：
  1. fs=1000;           %设置采样频率 1k
  2. N=1024;           %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;     %时间序列         
  5. f=n*fs/N;          %频率序列

  7. x1=sin(2*pi*50*t);      %噪声
  8. x2=sin(2*pi*200*t);     %信号
  9. x=x1+x2;              %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wc=2*125/fs;              %设置截止频率125Hz                 
  28. [b,a]=cheby1(2, 1, Wc, 'high');  %获取2阶IIR滤波系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');       %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x2.^2);           %信号的总功率
  44. Pu=sum((y2-x2).^2);       %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);     %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Matlab运行结果如下：
39.6.png

39.2.7 切比雪夫I型带通滤波器设计
    下面我们通过一个实例来讲解切比雪夫I型带通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将50Hz的正弦波当做噪声滤掉，下面通过函数cheby1设计一组带通滤波器系数，其阶数是2，通带为125Hz到300Hz，采样率1Kbps，通带纹波1db。Matlab运行代码如下：
  1. fs=1000;               %设置采样频率 1k
  2. N=1024;               %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;         %时间序列         
  5. f=n*fs/N;              %频率序列

  7. x1=sin(2*pi*50*t);      %噪声
  8. x2=sin(2*pi*200*t);     %信号
  9. x=x1+x2;              %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wn=[125*2 300*2]/fs;  %设置通带125Hz到300Hz                 
  28. [b,a]=cheby1(1,1,Wn);  %注意第一个参数虽然是1，但生成的却是2阶IIR滤波器系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');      %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x2.^2);          %信号的总功率
  44. Pu=sum((y2-x2).^2);     %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);   %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Matlab的计算结果如下：
39.7.png
从滤波的效果来看，2阶的带通滤波器效果不够好，出现这种情况的时候，需要大家去重新的调节截止频率，滤波器阶数和通带波纹。

39.2.8 切比雪夫I型带阻滤波器设计
    下面我们通过一个实例来讲解切比雪夫I型带阻滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成，将200Hz的正弦波当做噪声滤掉，下面通过函数cheby1设计一组带阻滤波器系数，其阶数是2，阻带为125Hz到300Hz，采样率1Kbps，通带波纹1db。Matlab运行代码如下：
  1. fs=1000;              %设置采样频率 1k
  2. N=1024;              %采样点数
  3. n=0:N-1;
  4. t=0:1/fs:1-1/fs;        %时间序列         
  5. f=n*fs/N;             %频率序列

  7. x1=sin(2*pi*50*t);      %信号
  8. x2=sin(2*pi*200*t);     %噪声
  9. x=x1+x2;             %信号混合

  11. subplot(221);
  12. plot(t,x);               %绘制原始信号
  13. xlabel('时间');
  14. ylabel('幅值');
  15. title('原始信号');
  16. grid on;

  18. subplot(222);
  19. y=fft(x,N);             %绘制原始信号的幅频响应
  20. plot(f,abs(y));
  21. xlabel('频率/Hz');
  22. ylabel('振幅');
  23. title('原始信号FFT');
  24. grid on;

  26. subplot(223);            
  27. Wn=[125*2 300*2]/fs;       %设置阻带125Hz到300Hz                 
  28. [b,a]=cheby1(1,1,Wn, 'stop'); %注意第一个参数虽然是1，但生成的却是2阶IIR滤波器系数
  29. % y2=filter(b,a,x);
  30. y2=filtfilt(b,a,x);      %计算滤波后的波形y2
  31. y3=fft(y2,N);         %滤波后波形的幅频响应
  32. plot(f,abs(y3));
  33. xlabel('频率/Hz');
  34. ylabel('振幅');
  35. title('滤波后信号FFT');
  36. grid on;

  38. [H,F]=freqz(b,a,512);
  39. subplot(224);
  40. plot(F/pi,abs(H));
  41. xlabel('归一化频率');        %绘制绝对幅频响应
  42. ylabel('幅度');
  43. Ps=sum(x1.^2);         %信号的总功率
  44. Pu=sum((y2-x1).^2);     %剩余噪声的功率
  45. SNR=10*log10(Ps/Pu);   %信噪比
  46. title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
  47. grid on;
复制代码
Matlab计算结果如下：
39.8.png
从滤波的效果来看，2阶带阻滤波的效果较好。

赞 评论
baiyongbin2009 回答时间：2015-4-27 11:05:13
39.3 椭圆滤波器的设计
39.3.1 ellip函数
功能：用来设计Elliptic(椭圆)型滤波器
语法：[b,a] = ellip(n, Rp, RS, Wn);
              [b,a] = ellip(n, Rp, RS, Wn, 'ftype');
说明：ellip函数与cheby1、cheby2函数类似，可以设计低通、高通、带通和带阻数字滤波器。参数RP和RS分别用来指定通带波纹和阻带波纹，Wn指定滤波器的截止频率，n为滤波器的阶数。
    与Butterworth和Chebyshev滤波器相比，ellip函数可以得到下降斜度更大、衰减更快的滤波器，但通带和阻带内均为等纹波。通常情况下，椭圆滤波器能以较低的阶数来实现指定的性能。
    [b,a] = ellip(n, Rp, RS, Wn);可设计n阶低通或带通滤波器。当Wn=[W1 W2]时，可设计带通滤波器。
    [b,a] = ellip(n, Rp, RS, Wn, 'ftype');可设计n阶高通或带阻滤波器。
    当ftype=high时，可设计截止频率为Wn的高通滤波器。
    当ftype=stop时，且Wn=[W1 W2]时，可设计带阻滤波器，阻带为W1<W<W2。

39.3.2 ellipord函数
功能：用来选择椭圆滤波器的阶数。
语法：[n, Wn] = cheb2ord（WP, WS, RP, Rs）；
说明：ellipord函数与cheb1ord函数类似，用于选择指定性能时的椭圆滤波器的最小阶数n和截止频率Wn，并与ellip函数配合可设计出最低阶数的椭圆滤波器。

39.3.3 椭圆滤波器设计
    关于椭圆滤波器的使用，大家参考前面的切比雪夫滤波器设计即可，使用方法基本是类似的。但是由于椭圆滤波器要同时给我通带和阻带的纹波，所以要得到满足要求的滤波器系数要花些时间去做测试。

赞 评论
baiyongbin2009 回答时间：2015-4-27 11:06:13
39.4 总结
    本章节主要讲解了巴特沃斯，切比雪夫和椭圆滤波器的设计，如果想用好还需要大家多多做测试，并深入了解相关理论知识。


赞 评论
拼命三郎 回答时间：2015-4-27 17:14:43
ddddd.png
赞 评论
stary666 回答时间：2015-4-27 17:45:39
支持原创。。。。
赞 评论
wamcncn 回答时间：2015-4-27 22:14:01
收藏学习
赞 评论

所属标签

关于
意法半导体
我们是谁
投资者关系
意法半导体可持续发展举措
创新与技术
意法半导体官网
联系我们
联系ST分支机构
寻找销售人员和分销渠道
社区
媒体中心
活动与培训
隐私策略
隐私策略
Cookies管理
行使您的权利
官方最新发布
STM32N6 AI生态系统
STM32MCU,MPU高性能GUI
ST ACEPACK电源模块
意法半导体生物传感器
STM32Cube扩展软件包
关注我们
st-img 微信公众号
st-img 手机版