1：PID控制原理
将偏差的比例（Proportion）、积分（Integral）和微分（Differential）通过线性组合构成控制量。用这一控制量对被控对象进行控制，这样的控制器称PID控制器。

01：模拟PID控制原理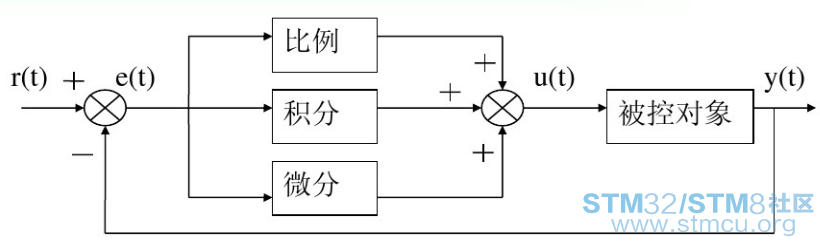

其中，r(t)是给定值，y(t)是系统的实际输出值，给定值与实际输出值的差值e(t)= r(t)- y(t)。e(t)作为PID控制器的输入。u(t)作为PID控制器的输出，也是被控对象的输入。所以，模拟PID控制器的控制规律为：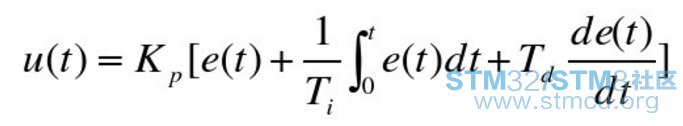

其中，Kp为控制器的比例系数；Ti为控制器的积分时间常数；Td为控制器的微分时间常数。

（1）比例部分：Kp*e(t)

在模拟PID控制器中，比例环节的作用是对偏差瞬间作出反应。偏差一旦产生，控制器立即产生控制作用，使控制量向减小偏差的方向变化。控制作用的强弱取决于比例系数Kp。Kp越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小。但是Kp越大，也越容易产生振荡，破坏系统的稳定性。

（2）积分部分
' p0 |' B* q1 s( X4 a从积分的数学表达式可知：只要存在偏差，则它的控制作用就不断增加。只有在偏差值为零时，它的积分才是一个常数。控制作用才是一个不会增加的常数。可见，积分部分可以消除系统的偏差。
积分环节虽然会消除静态误差，但是也会降低系统的响应速度，增加系统的超调量。积分时间常数越大，积分的积累越弱。这时，系统在过渡时不会产生振荡。但是，增大积分时间常数会减慢静态误差的消除过程，消除偏差所需的时间也较长，但可以减少超调量，提高系统的稳定性。
5 V3 n, E% I; x0 U9 h当积分时间常数较小时，则积分的作用较强。这时系统过渡时间中有可能产生振荡，不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定积分时间常数。
: b2 X5 v" E4 B/ m
积分系数（积分增益）是指：Ki=K_p/T_i 。
$ z8 w0 s# u0 N$ J& d# a: e, L/ Y（3）微分部分：Kp*Td*(de(t))/dt
7 B2 u0 k- y8 N' V9 r控制系统除了期望消除静态误差外，还要求加快调节过程。在偏差出现的瞬间，或在偏差变化的瞬间，不但要对偏差量做出立即响应（比例环节的作用），而且要根据偏差的变化趋势预先给出适当的纠正。为了实现这一作用，可以在PI控制器的基础上加入微分环节，形成PID控制器。
' e8 A! A! e# \- W微分环节的作用是阻止偏差的变化。它根据偏差的变化趋势（变化速度）进行控制。偏差变化的越快，微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入，有助于减小超调量、克服振荡，使系统趋于稳定。特别对高阶系统有利，它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感。对那些噪声较大的系统一般不用微分，或在微分起作用之前先对输入信号进行滤波。
微分部分的作用由微分时间常数决定。微分时间常数越大时，则它抑制偏差变化的作用越强；微分时间常数越小时，则它反抗偏差变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分时间常数，可以使微分作用达到最优。
微分系数是指：Kd= Kp*Td。

02：数字PID控制原理
因为在微机处理器里面是通过软件来实现PID控制算法的，所以必须将模拟PID控制器进行离散化处理，这样控制器只需根据采样时刻的偏差值计算控制量。因此，我们需要使用离散的差分方程代替连续的微分方程。假定采样时间T很短时（比如10ms），可以做如下处理：
! t4 \/ u) f/ q4 l: c% [（1）用一阶向后差分代替一阶微分；
# t; z6 K* r* ^' U$ S6 o5 G（2）用累加（矩形法数字积分）代替积分。
则有：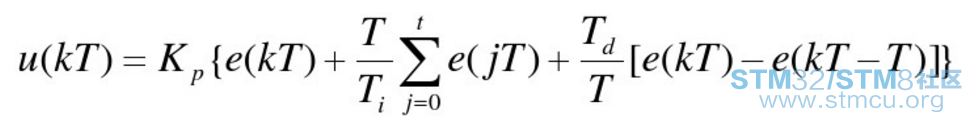

0 }4 F3 }# _7 j: J
2 ^$ f! |2 x$ m

数字PID控制算法分为位置式PID和增量式PID控制算法。

2：位置式PID控制算法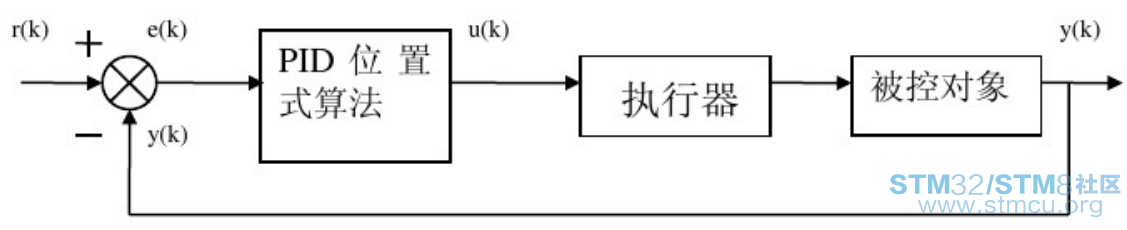

首先要对连续系统进行离散化：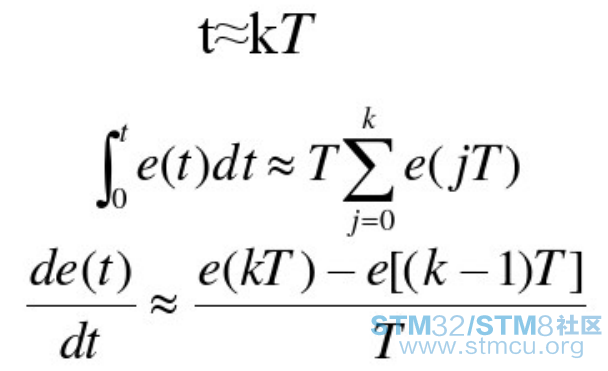

位置式PID控制器输出：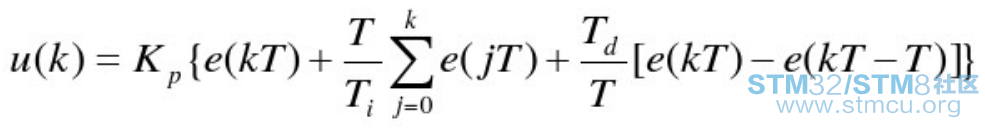

简化为：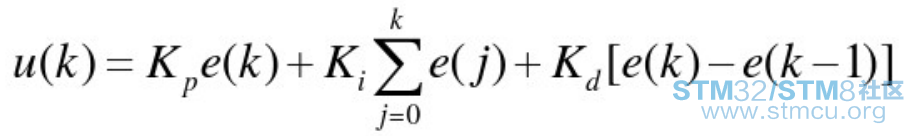

这种算法的缺点是：由于这种算法每次输出均与过去状态有关。计算时需要对e(k)进行累加，容易造成积分饱和，单片机运算工作量大。又因为单片机计算输出的u(k)对应的是执行机构的实际位置，一旦单片机出现故障，输出的u(k)将大幅度变化，会引起执行机构的大幅度变化。这样可能对执行结构造成严重的损害，在实际应用中是不允许的。增量式PID控制算法就可以避免这种现象的发生。

5 R* h( D0 H8 S* |- w

3：增量式PID控制算法

5 @* `5 D% L7 W, [$ ^' T; ~

+ W, _" Y6 U: X由位置式PID控制算法可以得到：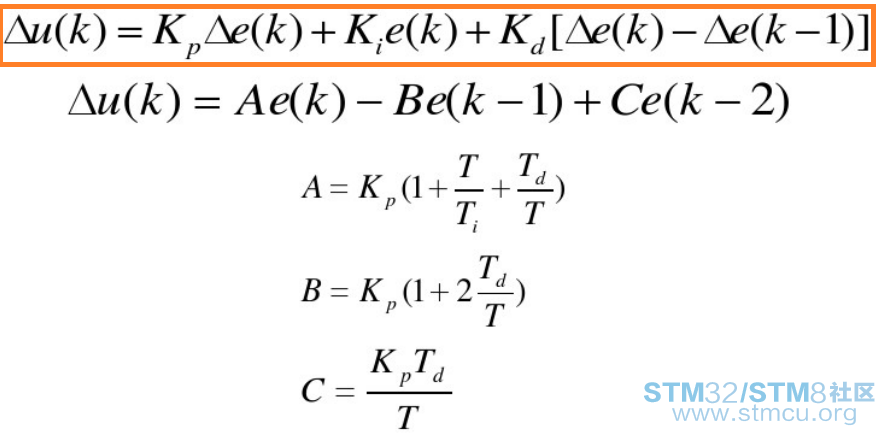
' {4 j6 U- P0 B2 z0 J" }3 l
则有数字递推PID控制算法：
u(k)=u(k-1)+△u(k)
增量式PID控制算法优点：
% J4 l; W8 a/ |* l4 H8 o（1）由于单片机输出是增量，所以误动作小；
（2）算法不需要累加，控制增量只与第k次的采样值有关；
7 t" \/ E! y5 }) u增量式PID控制算法缺点：
5 E" X; e* r1 @8 x, h积分截断效应大，有静态误差，溢出影响大等。
; ?$ B% U* G0 y+ {# Y, W


9 b5 t2 U% F9 }# i# K

之前发过的帖子

01：STM32定时器TIM1输出六路带死区互补PWM波形

02：STM32高级定时器死区控制

03：轻松搞定串口通信隔离
04：STM32中断优先级管理
& ~* U: n9 n6 b05：STM32单片机SWJ口引脚释放
3 F3 w: H. |; q( o& H06：真的明白Code、RO-data、RW-data和ZI-data吗？


更多内容请关扫码注微信号：



/ T) \4 q! @8 B* {

! \, \8 f5 N, H) I* u谢谢分享

谢谢分享

谢谢分享，简单明了

感谢详细讲解, 学习了