ST公司的STM32F411discovery开发板，就如何实现浮点FFT运算做个简单应用示例，并给些应用提醒。下面用到的IDE是ARM MDK。
" R5 z! }6 K  P6 T/ k$ C/ ^: C# f

7 z/ w+ p# r/ X因为要用到ARM公司提供的DSP库，所以需先开启一些必要的宏开关并添加相关库文件。STM32F4芯片支持DSP指令且自带浮点运算单元即FPU。


在MDK集成开发环境的相关配置栏添加__CC_ARM,__TARGET_FPU_VFP,ARM_MATH_CM4，并启用了硬件FPU。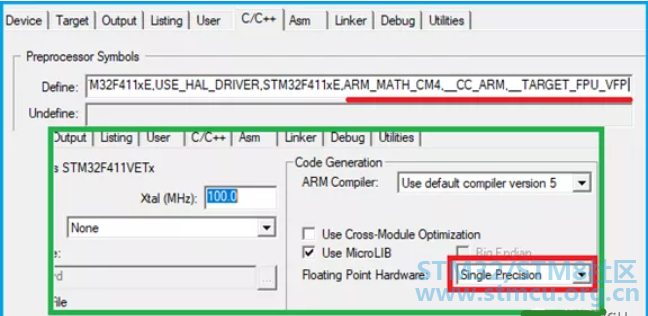
5 y4 m) j& g2 s9 B! ~: n

  E+ m5 c  u  w1 O1 |7 U' b2 p
, d$ ^5 X7 s+ v( U* O
- K" W1 h8 Q! I$ n: V
添加ARM提供的DSP库文件。如果使用STM32Cube库的话，该库文件一般在这个目录下【以STM32F4cube库为例】，有4个库文件。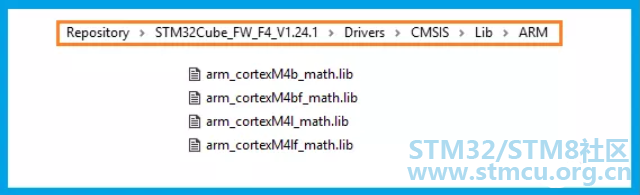
( M% q' y! H* k- V- E* C* }
4 p3 u. W- a% H
* [  x& w9 j' s2 x) K3 j

1 l5 j: L( S, D' y
$ q  g+ g0 B  @/ ^其中cortexM4b是基于大端存储模式但不支持硬件FPU时所用的DSP库文件，cortexM4l是基于小端存储模式但不支持硬件FPU时所用的DSP库文件。而cortexM4bf是基于大端存储模式且支持硬件FPU的芯片所用到的库文件，显然，cortexM4lf是基于小端模式且支持硬件FPU的芯片所用到的库文件。
, F. J0 w  P" P5 ?! |5 r2 w
) u7 T) D' c% d: l
; ~% D  x) D  _* j9 \这里我们添加arm_cortexM4lf_math.lib即可，STM32芯片采用小端存储模式，且STM32F4内置FPU硬件单元。

4 S2 z  |/ D# O
这里提醒下，首先，DSP库不要选择错了。其次，在添加.lib库文件时，添加时注意选择文件类型为lib。如果以别的文件类型强行添加进去后，编译可能提示出错。有时一会半会还找不到出错原因。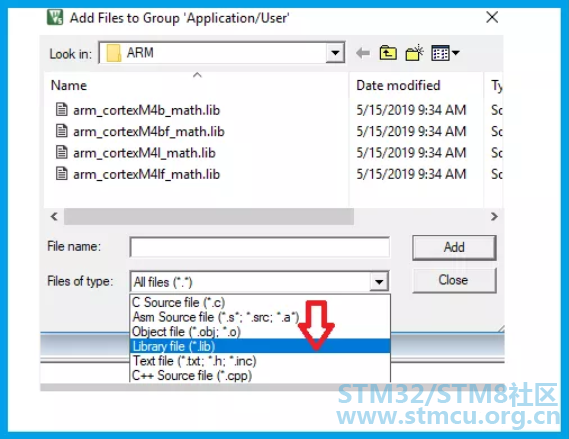



5 M* A; k) L; _" g
7 Q5 W+ }# k. D  Q
另外，我们还需在用户代码里添加包含文件：#include"arm_math.h"。至于其它头文件按需添加即可，比方math.h头文件。


下面开始看看具体的代码实现。
5 R2 G5 ?. k* N' }2 g

先做基本变量的准备及定义，比如用于FFT运算的点数，用于FFT运算的输入数据数组，输出数据数组、存放各频点初始相位的数据数组等。
+ l2 ~% ?2 Y& }8 N
' R/ P2 d) n- f! _
' G. s! @& @" L' K- I- a

# a, e% l2 \! K" f# i7 S+ X" d
( p5 y" ?9 [7 u1 u& B1 K; }这里使用几个正、余弦信号函数叠加产生一组信号序列。其中，有一个幅度为3的直流分量。另外几个分别是频率为200Hz、400Hz、600Hz、800Hz、1000H，幅度值分别是1、2、4、8、16的正、余弦信号函数。各输入数据项的虚部均设置为0。

+ W: t+ a" R% v% a6 E. K/ `: D



这里假设采样频率Fs=5120Hz，期望的最小频率分辨率为20Hz，则最小采样点数不要少于5120/20，即这里选择256点。【如果希望频率分辨率更高，可以加多采样点数】。


' F4 j% p! B$ O, U3 d其中，采样频率不得低于最高被采样信号频率的2倍。关于这个采样频率及采样点数的选择给几点提醒供参考：


1、采样点数它往往有个最小值需求，由采样频率和所期望的最小频率分辨率决定。
* a$ k# N1 p1 a5 s) i, X

% l& X2 d, b! ?/ \6 K! M2、整体上讲，增加采样点数有利于提高频率分辨率或改善运算结果。不过，增大样点数时既要考虑它对计算速度影响，同时还得考虑对微处理器内存的开销。比方128点和1024点的内存开销差别就较大了。

- b1 o, h2 Q- t" `
3、在选择采样点数时，除了考虑满足最小值要求外，还得结合具体选用的FFT相关函数类型，比方说是基4还是基2的。如果使用基4的FFT运算函数，则样点数须满足4的整数幂。如果使用基2的FFT运算函数，则样点数须满足2的整数幂。
2 H# j) Z7 k" ~7 s' S& u

$ e6 J4 J* Z5 Z7 ?4、具体到使用ARM的DSP库函数进行FFT运算时，还得遵循函数本身所支持的样点数约定，并不是你想多少就多少。比如，以下面函数为例：


$ b) D3 W3 T8 C( g) V

5 P; T3 ?5 p, a+ ]& x& v2 [
  z/ w2 K. f/ }基于上面FFT函数，如果你使用128点、512点、甚至高于1024点都不支持，或者说计算结果误差很大。【当你点数选择不当时，编译时目前是没有任何提示的。】


  Z1 n; O) f: O3 q, ?' X5、有些场合为了满足FFT运算要求，计算所需样点数可能多于实际数据量，这时我们在数据序列尾部补零凑齐。比方经过评估希望512点，结果实际数据才500个点，我们可以考虑补零以便于计算。这样做可以减小栅栏效应，但不会提高实际频率分辨率。


  u% ]/ y2 y2 H/ A+ H3 v3 ?/ Q7 h/ l5 a6、采样频率要满足不低于最高被采样信号频率的2倍的要求，但并非单纯的越高越好。一般取其3~6倍，具体应用时合理选择。

- \9 f; x- g) \5 r
关于采样点数的拟定就提醒这些，尤其上面的第3点、第4点，在使用相关函数时，最好看看函数原型说明。【注：我们在PC端使用诸如Matlab、Octave等数学工具时样点数往往可以做到比较随意、自由。】
  h# O+ K4 U7 {# S7 `4 C( f
4 Q6 l( t% S% s5 e! l
好，基本数据准备工作做完了，下面就是调用几个函数来完成FFT运算工作。
, R+ S" f! s9 Z, B  a

3 u, q0 B- ~, @+ {
' S* b. P" D+ t! ^, U# |
+ A" }: H8 x2 J0 e5 {. j
运行相关代码后，我们可以看到不同频点所对应的模值。


对于直流信号，其对应的频点位为0，计算出来的模值是其实际幅度的N倍，【N即FFT运算用到的样点数，这里就是256】，其它非直流频点的模值经FFT计算后的结果为实际幅度值的N/2倍。
1 A9 k+ S7 p% Z  C1 G

我们可以先使用Matlab或Octave模拟一下输出结果。下面是用Octave模拟出来的结果。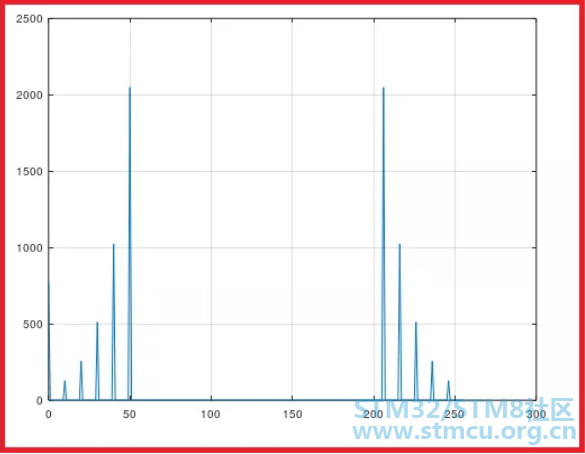
. ~/ c$ c, s9 }5 G  d
$ d- v3 Q3 B) |7 B


+ b4 S. T7 V/ G% k+ |8 `& \* a
% q6 g1 f7 W+ L( r因为经过FFT运算后的输出结果由对称的两部分组成，我们只需查看前面半部分即可。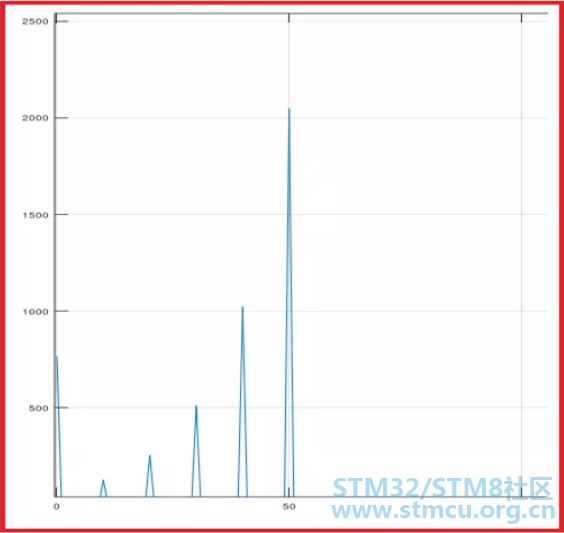
% n' `% O- f( N, p1 V, k

# k, [( @$ _5 K% h如下图所示：

$ N6 j! q4 A5 h  l) X

4 H9 a- b+ _0 j- ]% L$ j9 w
; {3 |' b; g+ J' X$ w3 V1 d
, d3 S4 ]2 x. C: T2 S, n8 q因为采样频率是5120，采样点数为256，即每两个采样点的频率间隔为20Hz.我们不难从上图看出直流分量0Hz以及200Hz、400Hz、600Hz、800Hz、1000Hz几个频点信号的位置及模值。图中0点位处所对应的模值就是直流分量的模值。因为各点位的频率间隔为20Hz，所以图中点位50处所对应的模值就是原信号中1000Hz余弦信号的模值。【前面提过了，FFT计算所得模值跟各频点信号实际幅度值还有个对应关系】


- Y5 c: r! o. q5 J! |! l我们再来看看经过STM32F4芯片进行FFT运算后的实际结果。计算后各频点的模值存放在数组fft_output[256]里，我们可以进行查看、比较。不难理解，如果点数越多，数组数据量也就越多，看起来并不太直观方便。我这里将FFT输出结果按照频点顺序在调试界面周期性地显示出来，如下图所示。其中，红色波形是信号频谱及模值，绿色斜线是频点递增变化曲线。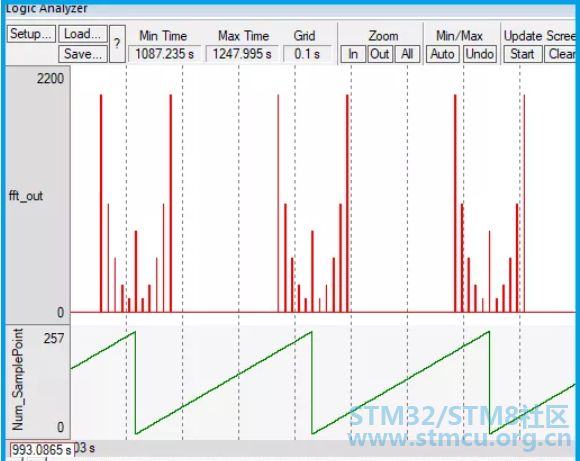




- S# R/ \) E  n# q
! {) p+ o, l! q2 E. X同样，我们只需查看FFT完整输出的前半部分结果。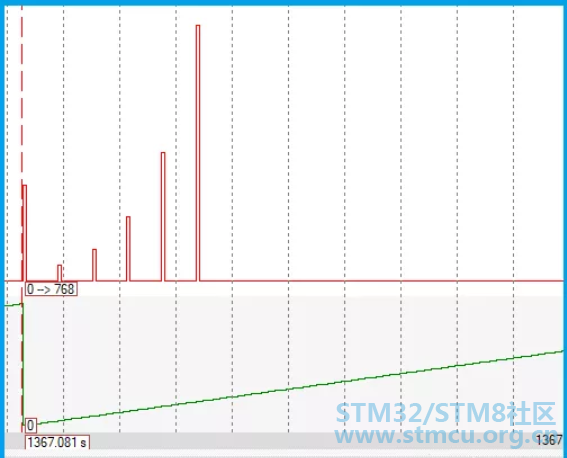

# p! z+ c$ y6 b* n* U( n! d
) C  @. ]$ E1 U1 `5 m7 q
! y, v; `6 w' A

! R0 ^7 K  h" }# R6 ~( L这里的零点处所对应的模值就是直流分量的模值，理论值应该为3*N，即3*256=768，实际计算结果也是768；其它5根线分别对应200Hz、400Hz、600Hz、800Hz、1000Hz这几个频点信号的模值。在显示界面轻点鼠标即可看到各处的频点位置及对应的模值。


- Z  M- P4 V0 |+ D当然，我们也可以到经FFT运算后的输出数组里去查看数据，相比之下，只是没有这么直观快捷。【下图是部分数据截图】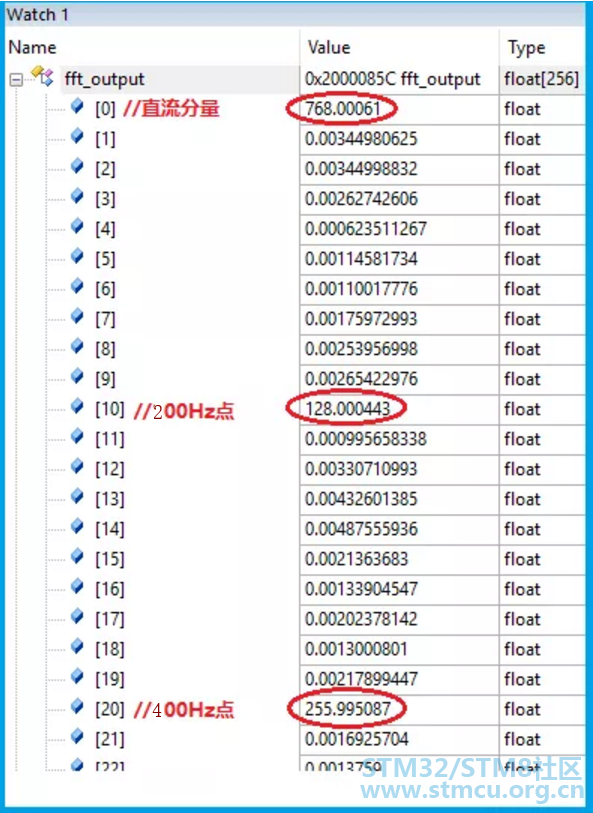
* S3 \2 b3 J3 b/ _& ?4 Q1 b) V. Q
" L0 j! x( g0 t( m' A7 b
3 U( [7 ]' n. N/ X0 x. X2 v9 m
7 G' ?9 N6 e0 s$ ?0 j6 _) h! t

5 O9 X1 K# L" x# N0 }. u+ j另外，我们还可以看看各个频点信号的初始相位值。同样，我们也可以先用Octave模拟运算结果。基于数学工具的运算结果如下：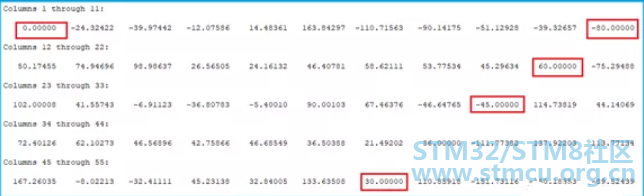
" i4 P4 p% z' z7 s3 X. g
# C4 p) o: ?+ ^! k# |


7 x7 B( F! z8 {; v
我们再看看基于STM32F4芯片的FFT计算结果：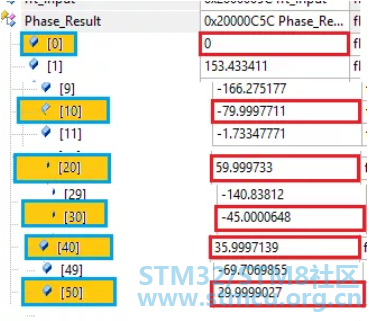



* w0 H1 K. a2 K  t4 [) Q2 a3 l

. |, B% a. r& p4 S5 {) V这里提醒下,初始相位的计算结果是按照余弦函数计算的，所以如果使用正弦函数产生的信号的话，就涉及到一个三角函数的转换关系sinx=cos(pi/2-x)，经过转换后所得的余弦函数的初始相位值跟计算结果就一致了。
; o8 R& Q, t+ K
1 W( }: g) E2 Q- J
# T, P- a; w2 Y, W" u. J2 y整体上，基于上面的参数所得FFT计算结果，跟理论值还是非常一致的。不过，要提醒的是，即使对于同一个被采样信号，因选取了不同的采样频率和采样点数做频谱分析时，可能会出现不同程度的误差。所以，为了减小误差，我们要选择合适的采样频率与采样点数，更多细节可以查看相关资料。

感恩，收藏

很专业，感谢分享！
+ G0 g" \1 x) l6 u( Z. M$ h% B