|
3 w1 r1 |1 q c' X 1 电机控制方案的分析与选择+ q: o$ x/ F! f$ a5 _% f( L# @ 在永磁电机的无感控制策略中，主要有两大类：（1）无感方波控制；（2）无感FOC控制。 $ S; d: h p2 b/ |/ I9 k 先谈谈无感方波控制。在无感方波控制中，主要是利用反电动势过零点的方式来得到换相信号（反电动势过零点的信号与电机的换相信号在相位上相差30°电角度）。为了得到反电动势过零的信号，通常采用两种方式：（1）硬件比较器法；（2）软件端电压采样法。这两种方法的原理大致是相同的，都是将检测得到的端电压的值与电机中性点电压进行比较来得到反电动势过零点的信号。在无感方波控制中，该检测手段的好坏将决定了控制性能的好坏。但无感方波控制通常会伴随着噪声大、转矩脉动大等缺点，因此仅在一些对电机无感控制要求不是很高的场合中较为适用。而无感FOC控制，主要是利用电机数学模型以及一些自动控制原理上的知识来实现电机的控制。在无感FOC的控制中，通常需要使用相应的观测器来实现对转子位置的间接得到。无感FOC常采用的控制策略有：（1）滑膜环观测器法；（2）隆伯格观测器法；（3）高频注入法等。滑膜观测器：利用自动控制原理中的滑膜变结构的控制原理来实现的。滑膜变结构实际上是变结构控制系统的一种控制策略，特点在于其控制的不连续性，在一定特性下迫使系统在规定的超平面上下做小幅度、高频率的运动，也就是我们常常讲到的“滑动模态”或“滑模”运动。此滑动模态与系统的参数和扰动无关，且可以设计，因此系统有很好的鲁棒性。隆伯格观测器：实质上是滑膜观测器的升维观测器，直接加入了反电动势观测量。高频注入法：利用的是电机的凸极效应来实现对转子位置的检测，该方法对电机的凸极效应要求较高，由于要注入高频通常会伴随着较大的电流啸叫声。目前，滑膜变结构的观测器策略已发展较为成熟，因此在目前的大多数无感FOC的控制中仍然采用滑膜观测器的方法对转子的位置进行检测来实现电机的FOC控制。3 j# `/ E1 C; T X$ l 2设计思路+ k/ W0 I3 u4 [' w. j o4 b1 N 我们这里主要描述的控制策略是滑膜变结构的无感FOC控制，同时在对该控制中所遇到的问题进行阐述，并在后面讲述针对这些问题的解决控制策略。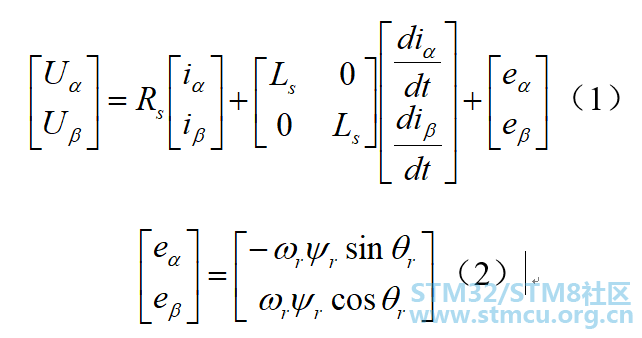 
2 R& w7 l! }* k1 T* H 从上面式（1）和（2）中可以看出PMSM在αβ坐标系的数学模型是含有相应的转子的位置的信息的，只需通过相应的手段得到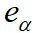 
和
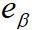
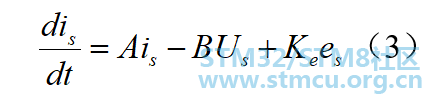
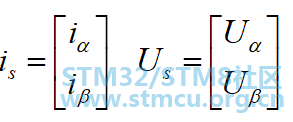
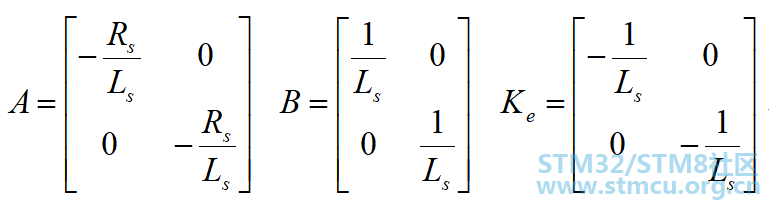
即可得到转子的位置信息。将上式（1）简化为：' U: u1 s' b2 M r7 D1 M- o1 n0 K9 o
滑膜变结构控制的定义： 设有一控制系统：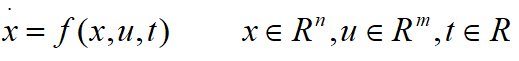 
求解控制函数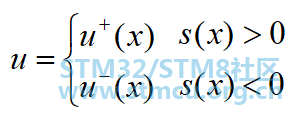 
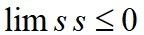
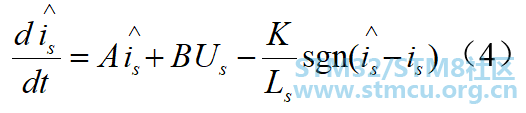
当切换函数满足： 5 ~% |& m5 N5 C9 h 
式（4）中是
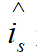
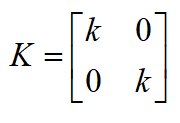
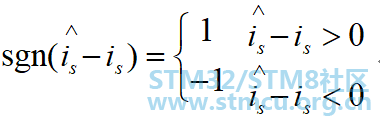
% ]$ d+ D& h- h! F1 h1 k 将（3）-（4）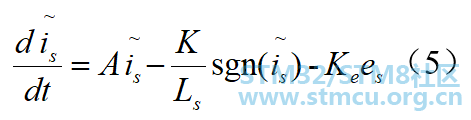 
$ S, D2 ^& Q! N0 ^+ v. ` 选取滑膜面
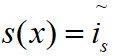
% C2 ]; m- t1 W6 Q! _! v 3控制策略分析 针对上面分析的，PMSM的滑膜观测器额无感FOC控制框图如下：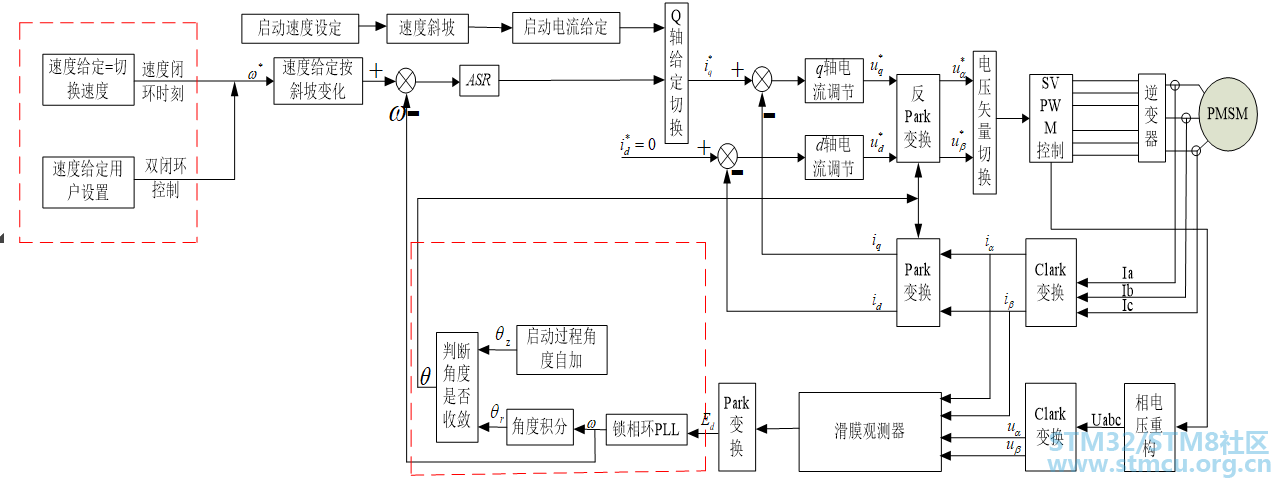 
▲ 图1：PMSM的滑膜观测器的无感FOC控制框图 ( \0 Q! h9 V. p, Z m8 q4 P从上面图一的控制框图中可以看出，在此控制中有三点是该控制需要重点解决，其分别为：（1）转子初始位置辨识；（2）无感FOC的启动；（3）如何实现平滑切换。. a8 \/ |7 D3 ]$ K7 H g1 g 我们逐一分析：4 E. b& M& F& l A7 f: \ （1）转子初始位置辨识：采用基于电感饱和特性的电流差值检测法：由于电感的饱和效应，电感值的大小随转子位置近似成正弦状变化。绕组电流响应与电感的大小存在相应的关系，永磁同步电机静止时，对任意两相绕组注入幅值恒定的电压脉冲，此时线圈绕组可看成RL串联电路的零状态响应。电流大小反映了绕组的电感大小，同时也包含了当前转子位置信息。根据电流响应的值可以辨识出转子初始位置角。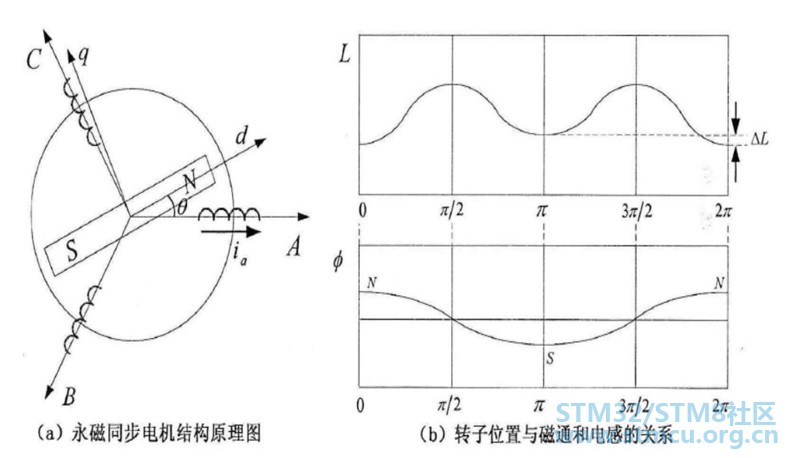, ?( N3 `. p5 v+ L$ Q( v1 ~ F 
▲ 图2：转子位置与电感和磁通之间的关系 在PMSM中按照如下顺序注入6组脉冲，如图3所示。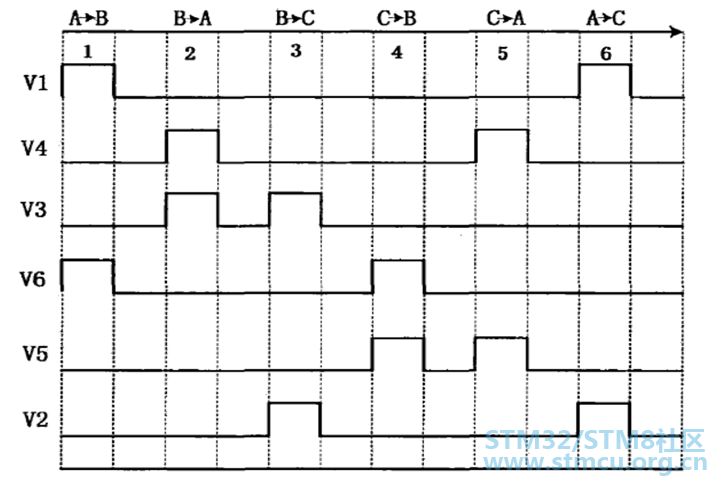 
▲ 图3：注入脉冲顺序 则注入的脉冲在绕组上的电流示意图，如下图4所示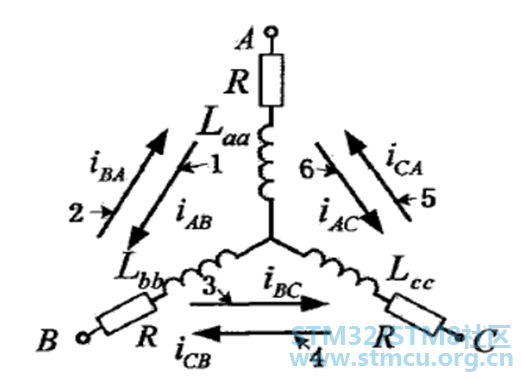：2 q" d6 F$ D8 T' @8 n7 ~# u4 Z 
▲ 图4：注入的脉冲在绕组上的电流示意图 以在AB绕组上的电流相应分析，其电流相应如图5所示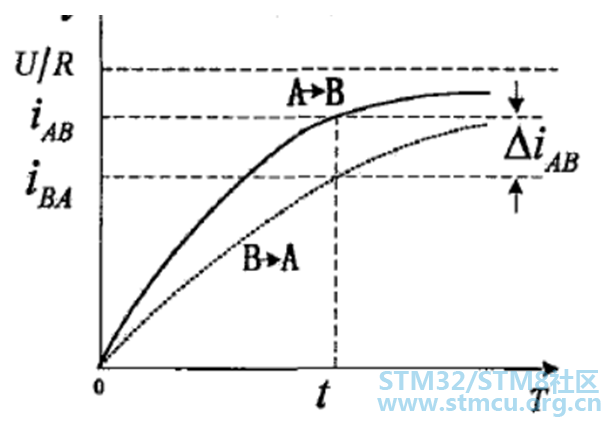：! h# B5 g+ C% y7 m u; X v 
▲ 图5：AB相绕组的电流相应图 又由于转子的位置与线电流的差值之间存在着如下图6的关系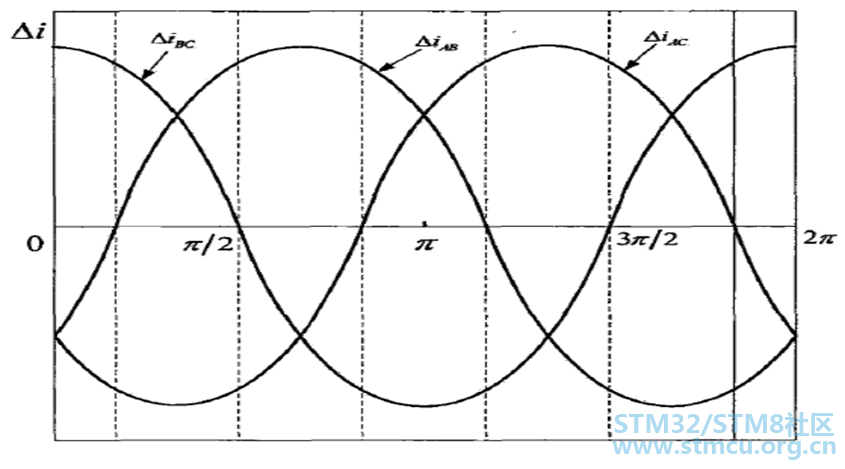： $ s! [7 f3 ~6 `% t# P* y 2 K; i( Q0 f2 F0 ]3 z6 }/ I3 f8 B
▲ 图6：注入脉冲后线电流差值与转子位置之间的关系 7 ]7 s% Y# T5 g; E3 o 通过上面的分析通过如下公式即可得到转子的初始位置：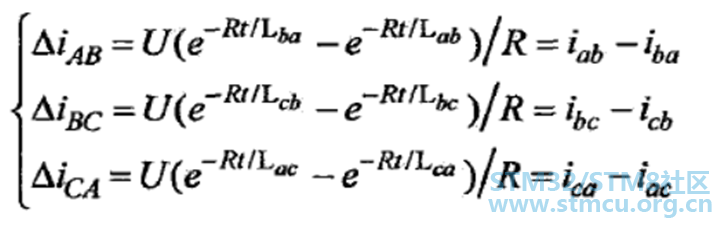 
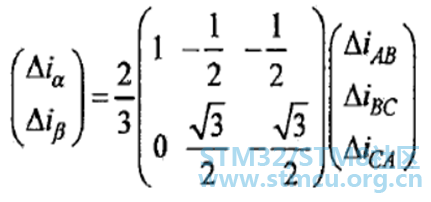
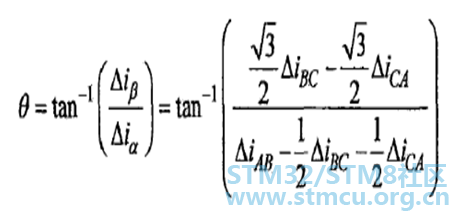
) T# Y+ B. [! @3 ?7 l% v5 u 
% G+ ]+ a+ X7 N8 e/ o4 i3 c6 s, k: J 
1 [! m2 X5 z# v; u. m （2）无感FOC启动：在无感FOC的启动中，通常采用的时三段式启动方法，在有的情况下也采用V/F进行启动，但是这些启动都具有相应的局限性，对于无感FOC的控制中，其启动的性能将对PMSM的无感FOC控制有着重要的影响，这里讲述一种I/F比的启动控制策略。 $ I" C0 c& K; G- [+ K I/F启动方式的基本思想是在电枢绕组中产生幅值跟随参考值、频率逐渐增大的旋转电流矢量，使转子加速起动。它的特点是工作在速度开环、电流闭环的状态，定子绕组电流经过坐标变换以后，投影到由指令位置角决定的旋转坐标系上，并受期望值的约束，可有效避免过流产生。其控制框图如下图7所示。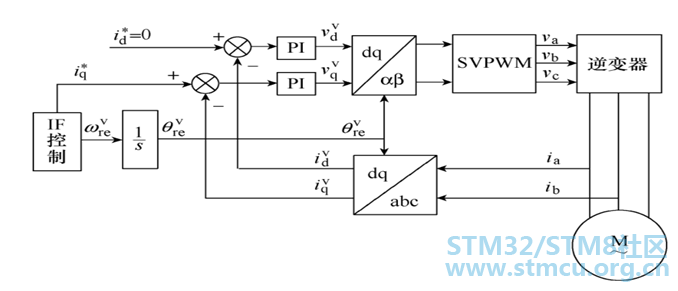 
▲ 图7：I/F启动 （3）如何实现平滑切换： 在前面的I/F启动控制中，其中电流已经处于闭环状态，速度为开环，当滑模观测的角度和速度收敛时，为了实现其平滑切换，这里讲述一种基于双DQ轴平滑切换的方式。双dq空间切换的瞬间需要完成如下几步操作： % @3 x6 q0 a& p- E9 t% } 第一步: 电流环的反馈变量由dvqv空间下的idv和iqv转换为dq空间下的id和iq。 6 L6 z2 f) ~* j4 y; J 第二步：d轴电流定由0转换为 iq*sinθL，q轴电流给定由iq*改为由转速环PI调节器生成，而转速环PI调节器的输出初始化为 iq*cosθL。 ; N% u$ ~# f9 f* u 第三步：dq轴PI输出初始化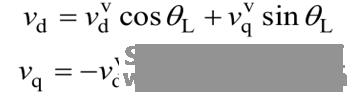 
第四步：改由dq空间进行坐标变换和逆变换。 双dq变换的模型图以及控制框图如下图8和图9所示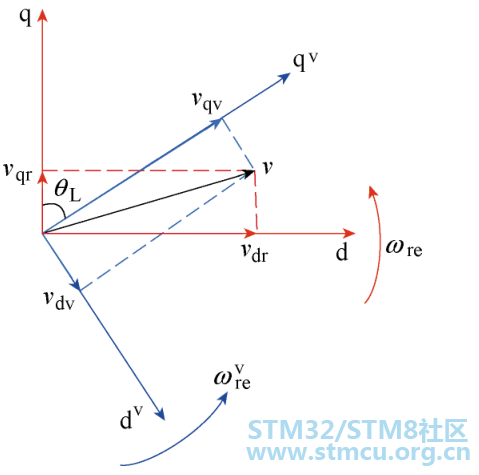： ! B4 n! r1 {& M$ J- a- ~5 M 
▲ 图8：双dq变换模型图 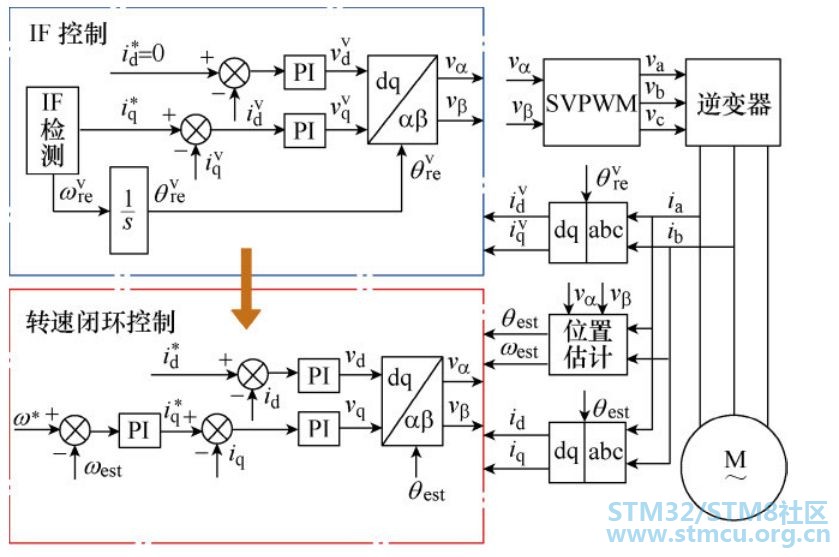9 x1 S u* g- e 
▲ 图8：双dq变换的控制框图 * Y0 ^$ h6 o' g* ]6 w0 s 4程序编程与调试 上述完成了对PMSM的滑膜观测器的无感FOC控制的原理分析以及重难点分析，接下来完成对上面控制策略的编程。其程序主要分为： （1）启动程序： 
" s, J8 K) Z7 [! b8 J/ l3 k% a- N （2）SVP程序： - Y; S( n: O, W2 f5 O) A
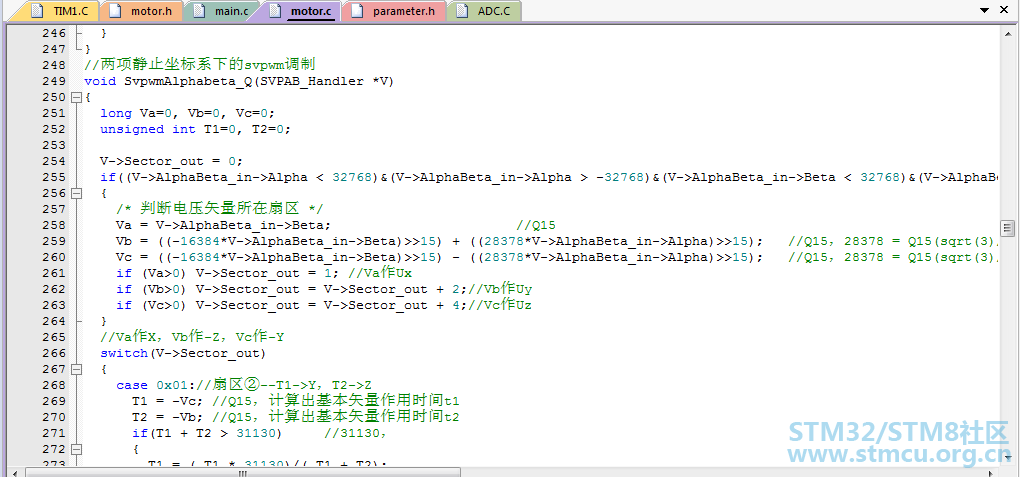
% d2 r7 o% }) } （3）相电压重构程序： 
（4）ADC中断服务子程序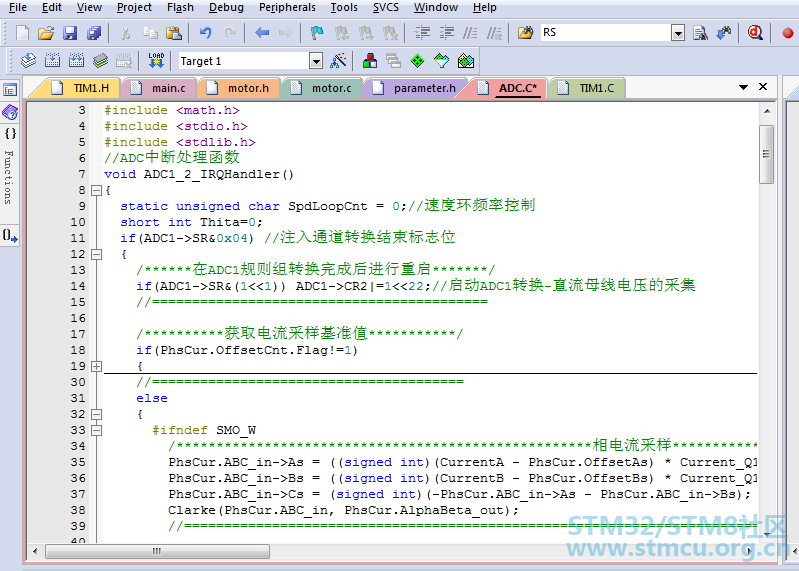： * H# ]" {, Z* F$ B4 R
6 A9 j- x% n: u/ q) r0 [7 d8 H$ x2 Y （5）滑膜观测器算法程序： 
: G L; @ E2 ]) @" G5 J! P { （6）锁相环程序： 
最后，讲下在编程调试过程中的难点： （1）开关函数和开关增益的选取，这个将会影响着观测器的好坏，通常通过串口打印出eα和eβ的波形来进行调试； （2）eα和eβ的滤波，该滤波深度不能太大，通常取0.5左右，但是具体的滤波深度还是需要通过串口打印出反电动势波形来进行调节； 6 Z! g s1 S/ p( x （3）PLL的KP和KI的确定，锁相环的输出的快速性与稳定性将会影响着观测得到角度的线性度和稳定性，因此对于锁相环的参数的调节是至关重要的，通常需根据观测器输出的角度通过串口打印，来做相应的调整； + j( p: \4 ]# `3 M （4）数据格式的处理，在电流采样时，最好将ADC采样的电流转化成实际电流再进行相应的Q格式，但是在这里Q格式的大小也会对系统有着重要的影响，需要在在实际的程序调试中注意。 |
微信公众号
手机版
大佬，在第3部分控制策略分析里，转子初始位置辨识是做什么用的没看明白，IF启动时不是不需要考虑转子的实际位置吗，d轴给定一个电流吸到位，然后IF启动不就可以了吗？求指点