
|
[导读] 生活环境周围信号万万千,对于一个嵌入式er。我们利用技术去了解世界、改变世界。而一个产品要与外界物理环境打交道,一个至关重要的触角就是采样真实模拟世界的信号,翻译成芯片可理解的数字信号,进而实现很多为人服务的应用产品。那么提到采样,ADC技术你绕不开,今天总结分享一下ADC的点点滴滴。 & f% p; a% r) A* s 啥是ADC/ h! C7 @" D$ L$ h" G8 P ) V2 X) d. j2 ?9 b, O% O 在现代电子工业技术中,模数转换器(ADC, A/D,或A-to-D)是一种将模拟信号转换成数字信号的系统。ADC还可以提供隔离的测量,例如将输入模拟电压或电流转换为表示电压或电流大小的数字的电子设备。通常情况下,数字输出是一个与输入成比例的二进制补码,但也有其他的可能性。举些栗子:
: e- Z" q6 m' i# @6 gADC的性能主要由其带宽和信噪比(SNR)来表征。
整这么多文字还是不直观易懂,到底啥是ADC,来个会动的图吧:3 K) p, z! [$ w6 b9 _ 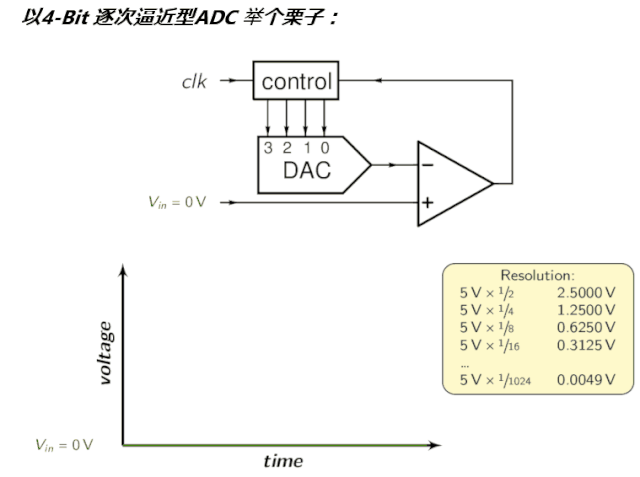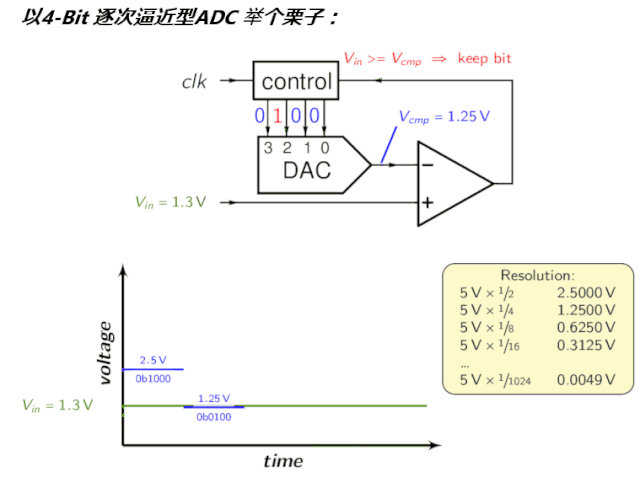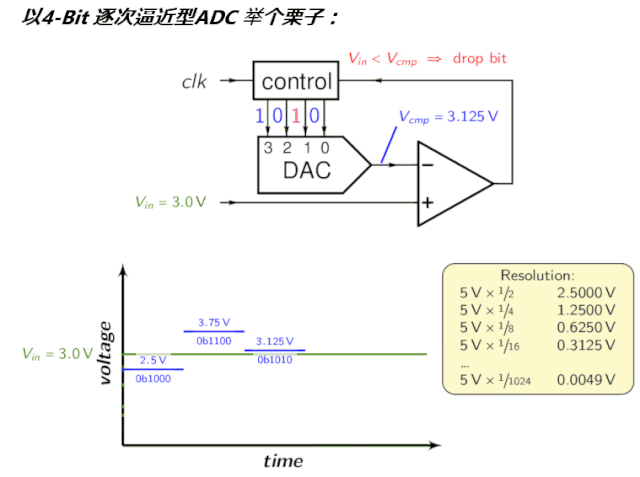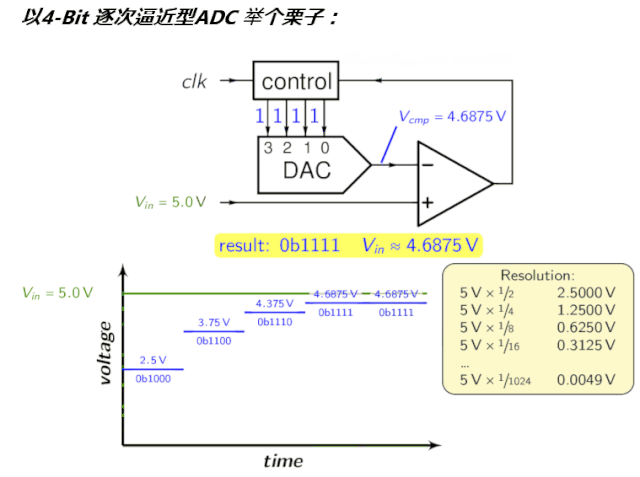
+ s$ E0 |; e4 }+ | 须理解的指标分辨率$ p) Z. _& V7 d+ S, A" a ADC看成一个黑匣子,基本的有一个模拟输入及其等效数字输出。下图 所示示例为一个N位ADC。N通常是6到24之间的任何值,常见的是8、10、12或16位。参考电压可能为单端电压,也可能为一个~,是一个正负电压参考源。 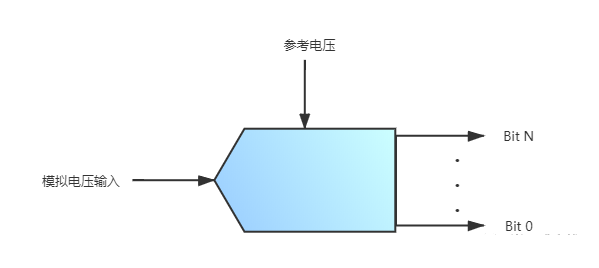
输入是一个模拟电压,范围从0到参考电压,参考电压取决于实际ADC及外围电路。假设使用N位,则可能有个可能的数字输出值,则1位表示的值为。在很多书上也称这个指标为LSB(Least Significant Bit)。 这便是分辨率的概念。模数转换器的分辨率表示在模拟值范围内它可以产生的离散值的数量。该分辨率决定了量化误差的大小,因此决定了不使用过采样的理想ADC的最大平均信噪比。举个栗子,如果给定ADC的最大输入值为5.0V,而ADC为10位类型,则每一位表示 
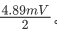
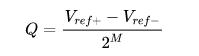
/ h/ Q% c, U1 [6 }! ?! A 其中 
0 K. e/ I. m0 o 量化误差 9 V# Z1 G+ a/ W/ [/ y 量化误差是由理想ADC中的量化过程产生的。由于ADC的模拟输入电压与输出数字化值之间的存在舍入误差。 在理想的ADC中,量化误差均匀地分布在和之间,并且信号具有覆盖所有量化水平的均匀分布,因此信号量化噪声比SQNR(Signal-to-quantization-noise ratio)定义为:9 B3 t. j4 E# J1 S% t 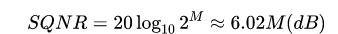
, c$ t$ `. F& c. C% W$ s' w# R3 n 其中,M为ADC的位数,M位数越大或越高,SQNR也越大。6 x% u; q$ S* P: o% g1 A ( |) s: Z2 K: V3 v* _8 S 精度$ |1 n/ l' J0 q& M- O, a2 D 2 E+ n) s$ Q' x 量化误差和非线性是模数转换器所固有的误差指标。用最低有效位(LSB)的单位进行度量。比如一个10位ADC, 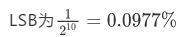
: \) u& _& A) v$ |3 w( M* ^# F 非线性度 $ i% ?( U& _ `0 k; ^. S 实际使用的ADC除了上面说的量化误差外,还具有更多的误差源:3 G# R4 L, z- D5 b+ e
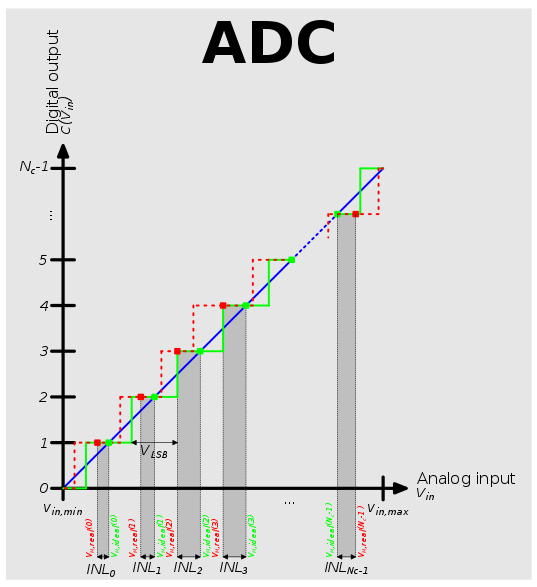
0 { y% Z* X* {3 M' Y5 r/ X5 n 所有ADC都存在由其物理缺陷引起的非线性误差,导致其输出偏离其输入的线性函数(或其他函数,在故意使用非线性ADC的情况下)。这些误差有时可以通过校准来减轻,或通过测试来避免。所谓校准,比如可以通过量点线性校准,假定y为ADC数值,x为输入模拟电压:; E1 w4 m" \$ p" @6 G 
应用实施策略:将上述k/b,利用两个点进行校准,将校准数据k/b存储在非易失存储器中。补充说一下:工程实践中需要校准的原因还因为选取的外围电阻、电容器件都有误差,所以这也是另一个需要标定的重要原因。 s' C2 m5 Y. _; j/ G+ y; e+ x采样率- y- z P# q- U: _4 K& P 模拟信号在时间上是连续的,因此有必要将其转换为数字序列,这是数字信号处理的基础。因此,需要定义从模拟信号中采样数字序列的速率。该速率称为转换器的采样率或采样频率。可以采样连续变化的带限信号,然后可以通过重构滤波器从离散时间值中再现原始信号。奈奎斯特-香农采样定理表明,只有当采样率高于信号最高频率的两倍时,才可以忠实再现原始信号。个人在使用时,一般会选4倍以上。由于实际的ADC不能进行瞬时转换,因此在转换器执行转换期间(称为转换时间)输入值必须保持恒定。一个被称为采样保持电路——在大多数情况下,它使用一个电容来存储输入端的模拟电压,并使用一个电子开关或栅极来断开电容与输入端的连接。许多ADC集成电路包括内部的采样保持电路模块。图中的T为采样周期,其倒数就是采样频率。 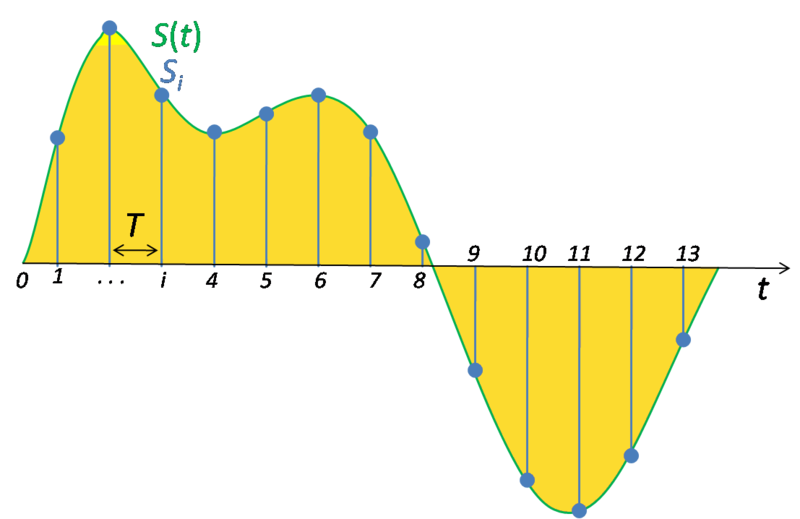
! U4 b3 N. M4 R8 v5 Y- G 混叠 8 O6 y0 Z% X' m ( ?$ Y6 W' }- A: w/ I ADC通过在不连续时间间隔(离散的含义)内对输入值进行采样来工作。假设以高于奈奎斯特速率的频率对输入进行采样(定义为有用信号频率的两倍),则可以重构信号中的所有频率。如果对高于奈奎斯特速率一半的频率进行采样,则会将它们错误地检测为较低频率,这一过程称为混叠。之所以会出现混淆,是因为每个周期对函数进行两次或两次以下的瞬时采样会导致丢失周期,从而出现频率错误地降低的情况。例如,以1.5 kHz采样的2 kHz正弦波将重构为500 Hz正弦波。 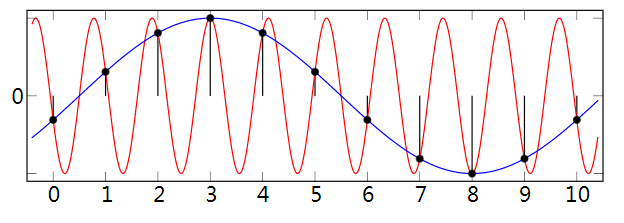
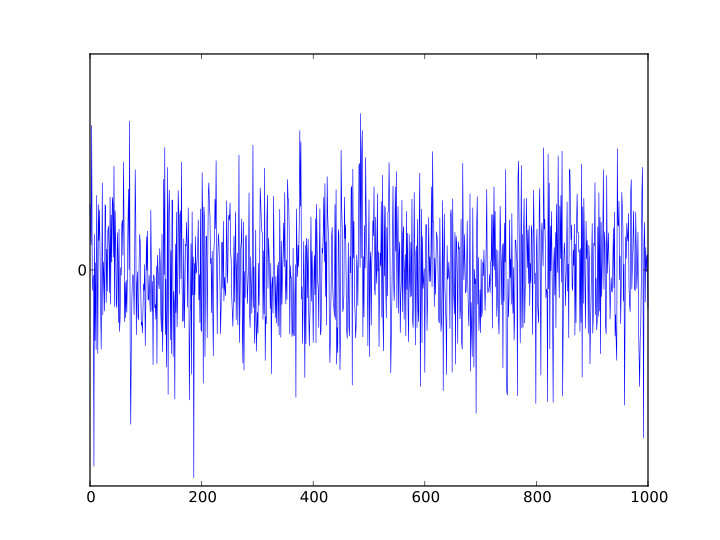
9 G0 w8 A1 |& r/ Q9 q) o) I ! o/ p" F+ ~9 J5 g( l' x- m6 t 为了避免混叠,ADC的输入必须经过硬件低通滤波,最简单的实现形式为一阶无源RC滤波网络,以去除采样率一半以上的频率。这种滤波器被称为抗混叠滤波器,它对于实际的ADC系统至关重要,该系统适用于具有更高频率内容的模拟信号。在需要防止混叠的应用程序中,可以使用过采样来大大减少甚至消除混叠。( P4 X# O! Q) A. _ a 例如:六种不同采样速率采集的数字序列重建的4种波形。其中两种波形在采样率足够情况下未出现混叠。另外两个说明了在较低速率下会失真(混叠增加)。 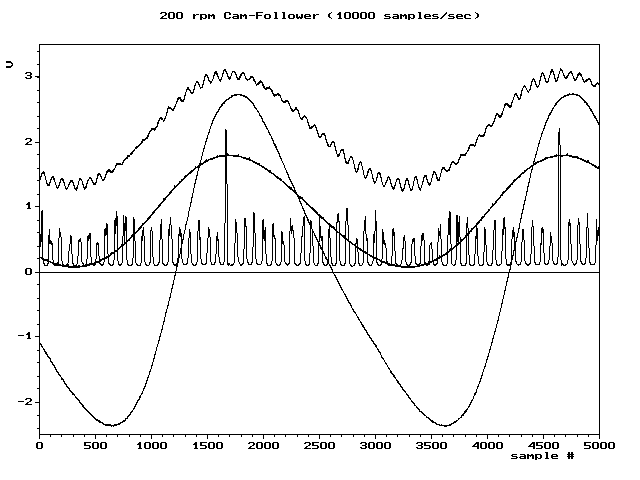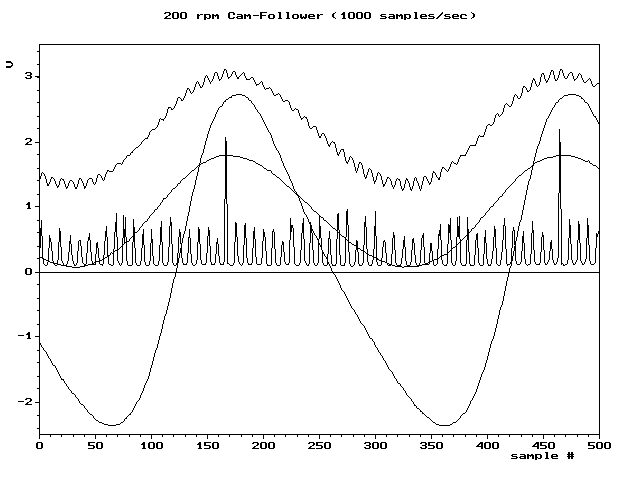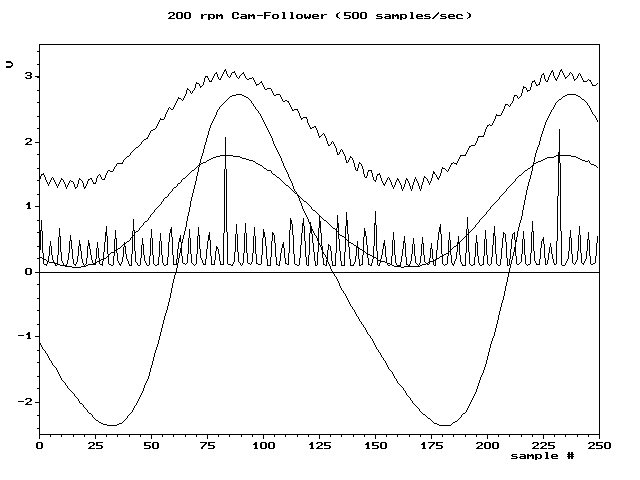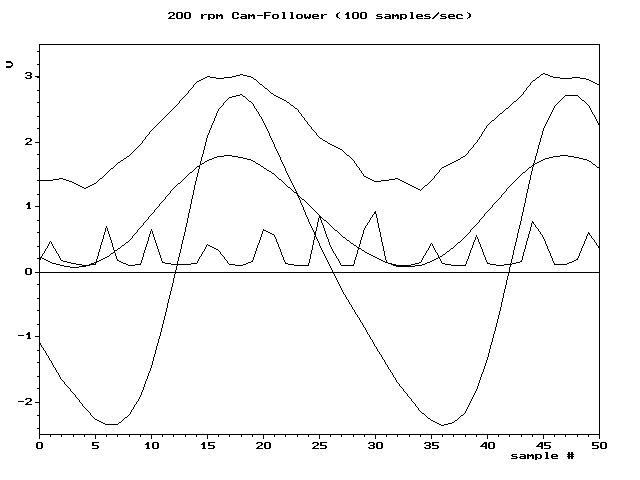
过采样& T" j1 t( y/ ~5 ~0 P . C2 e- l9 t8 {9 O8 Y1 p/ T 为了经济起见,通常以所需的最小速率对信号进行采样,结果是引入的量化误差是白噪声在转换器整个通带上的扩散。如果以远高于奈奎斯特速率的速率采样信号,然后进行数字滤波以将其限制为信号带宽,则会产生以下优点:
( i( k: t& `9 V* Z3 W 过采样通常用于音频ADC中,与典型晶体管电路的时钟速度(> 1 MHz)相比,所需的采样率(通常为44.1或48 kHz)非常低。在这种情况下,可以以很少的成本或不增加成本就可以大大提高ADC的性能。此外,由于任何混叠信号通常也都在频带外,因此使用非常低成本的滤波器通常可以完全消除混叠。下图比较直观,可以看出提高采样频率,可以更为真实的重建原始信号,而采样频率低些,对于信号的细部则无法准确重建。 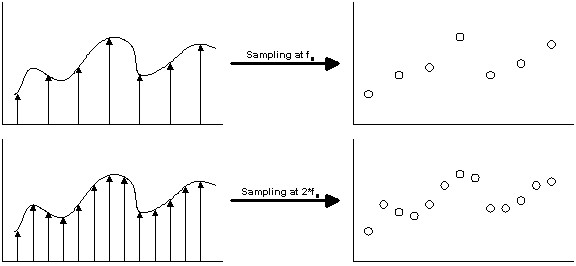
9 G2 d+ U, i8 d ADC类型积分型ADC 9 y7 ^# A$ o1 x4 s. u 优点:
单斜率积分ADC 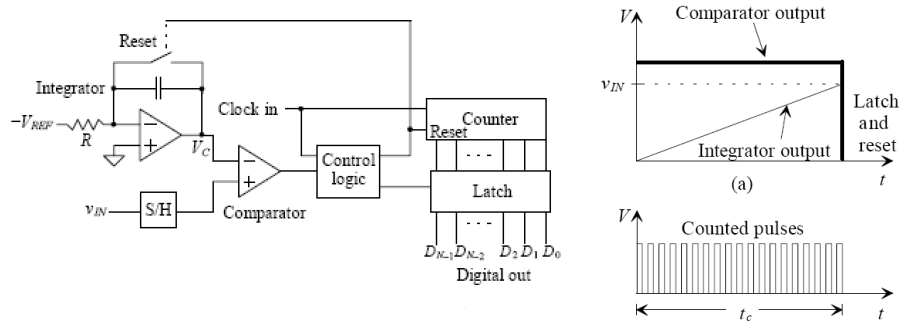
# r6 M7 Z$ s) Q/ T ]$ [2 R! z; i* V # K% X2 x0 |8 m' H/ n/ x2 V 比较器将输入电压与集成基准电压的值进行比较(请注意,由于已连接至运算放大器的反相输入,因此我们将设为负)。同时计算时钟周期数。当积分器输出等于时,比较器输出逻辑“ 0”,触发计数器和积分器复位,锁存器保持数字输出。+ u- K$ T! Y1 K 这就是转换时间,知道为啥说这种积分型ADC慢了吧。来看下最差的情况吧,假设输入电压,假定,假定是20位ADC,那么! 0 I3 @ |' I, ^$ o" H ; C1 T1 w: R' {0 S& R: G/ K 双斜率积分ADC8 F+ F# G* K# M7 K 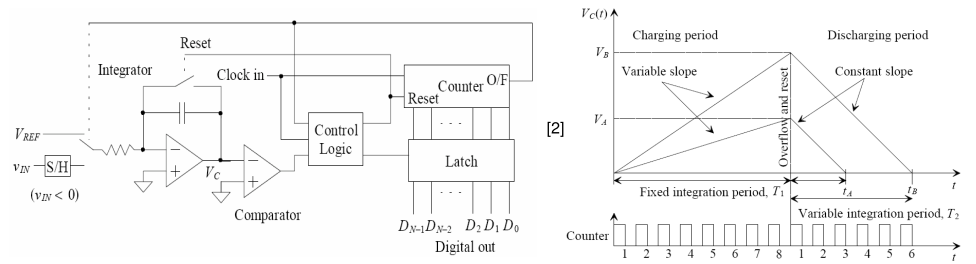
双斜率ADC与单斜率ADC的不同之处在于,现在将与地进行比较,并集成了两个电压和。刚开始时,负输入连接到积分器,使斜升直到计数器溢出。由于在反相输入会切换到一个负值进行积分,因此积分器输出将始终为正且大于零,因此计数器将继续运行直到溢出为止,这需要2N个时钟周期(= T1)。5 f! T; v) x5 k6 U0 ]9 a' u 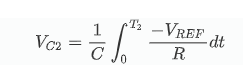
在T2时刻,将等于与之和,且为0,也即:0 t. {1 ^7 g6 F8 X3 m* C 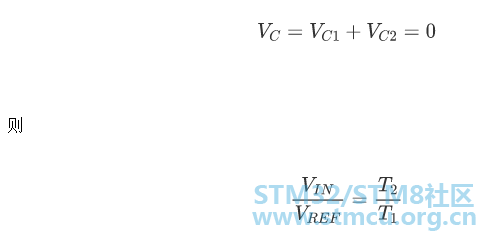
& D% J- ~. `8 n+ D- b) g4 g 因此,即为ADC转换的原理,双斜率比单斜率ADC更慢,由于执行了两次积分, 与积分器斜率相关的误差将被抵消,从而从原理上提高了精度。1 C) T% K ^# k9 W+ h + t& K" r2 g7 a q Sigma-Delta Σ-∆ ADC ! I& ^. r( \" O; a! p/ Q 3 y: D2 G, A V a! g: c% v3 O! M 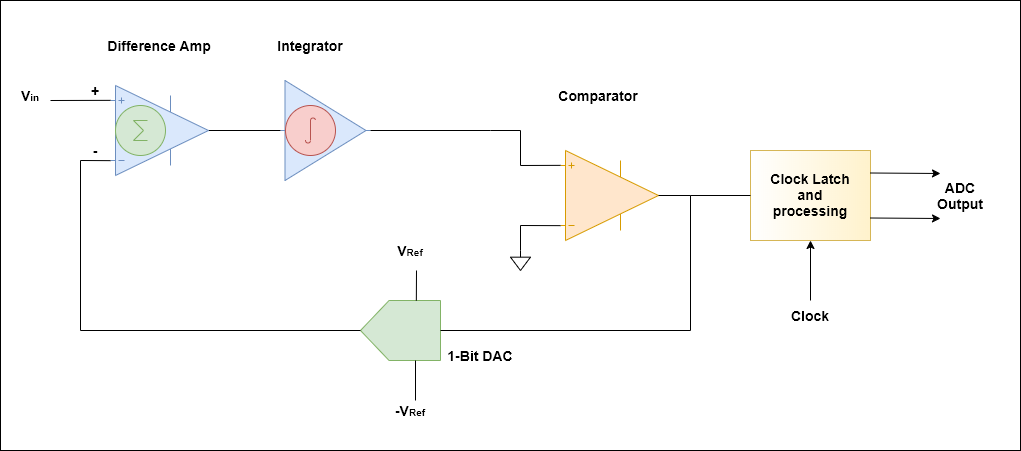
- J1 k7 \7 K- [6 t4 d 
Σ-∆ ADC 对所处理信号进行过采样(这个概念见模数采样知多少),并对待处理信号进行低通滤波。通常,在过滤器之后使用Flash ADC转换的比特数小于所需的比特数。所产生的信号连同由FLASH离散电平产生的误差,被反馈回并从输入中做差然后输入到滤波器。这个负反馈的可对噪声形成抑制作用,使它不出现在期望的信号频率。ADC之后的数字滤波器(利用抽取滤波器)可降低采样率,滤除不想要的噪声信号并提高输出分辨率(故称为sigma-delta调制,也称为delta-sigma调制)。# J; K; b5 Q+ KFlash ADC也称直接比较型 FLASH ADC的原理可能是最容易理解的。下图是一个两位ADC的示意图,由许多比较器组成,每个比较器都被提供了比上一个基准值高一个位值的基准电压。因此,对于一个8位ADC,需要256个这样的比较器。对于10位,则需要1024。/ D' P1 O! w( r 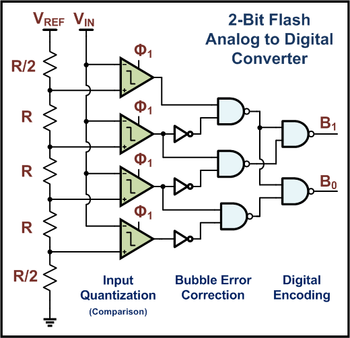
2 H" E, F5 B2 p- o, ~" d FLASH ADC(直接比较型)速度很快。它直接转换输入,而不需要任何采样或繁重的后期处理。问题是,它需要很多比较器,而且很多比较器占用了芯片上的大量硅空间。因此,只有在需要其他ADC实现方法无法达到的极高速度时才使用Fash ADC。; g( H5 Q3 {3 u& m5 |# Y / I/ Y/ H( A7 s# Y* H8 ?% B 二分法在硬件中体现 实际应用中,还有一个变种比较常用,半 FLASH ADC。它使用两步的过程来减少实际转换链中所需的转换器数量:
逐次逼近寄存器SAR7 D3 L; S( a8 U6 y% i$ x; A $ D$ E% M4 H2 q g" s 逐次逼近寄存器(Successive Approximation Register):逐次逼近ADC使用比较器逐次缩小包含输入电压的范围。在每个连续的步骤中,转换器将输入电压与内部数字与模拟转换器的输出进行比较,后者可能表示所选电压范围的中点。在这个过程的每一步,近似都被存储在一个逐次逼近寄存器(SAR)中。例如,假设输入电压为6.3 V,初始范围为0到16v。对于第一步,输入6.3 V与8v (0-16V范围的中点)进行比较。比较器报告输入电压小于8v,因此SAR被更新为将范围缩小到0 - 8v。第二步,将输入电压与4v (0 - 8v的中点)进行比较,比较器报告输入电压高于4v,因此更新SAR以反映输入电压在4 - 8v范围内。第三步,输入电压与6v比较(4v与8v的一半);比较器报告输入电压大于6伏,搜索范围变为6 - 8伏。继续这些步骤,直到达到预期的解决方案为止。其拓扑结构如下,$ g, m. F5 x7 w$ j: G3 T2 l 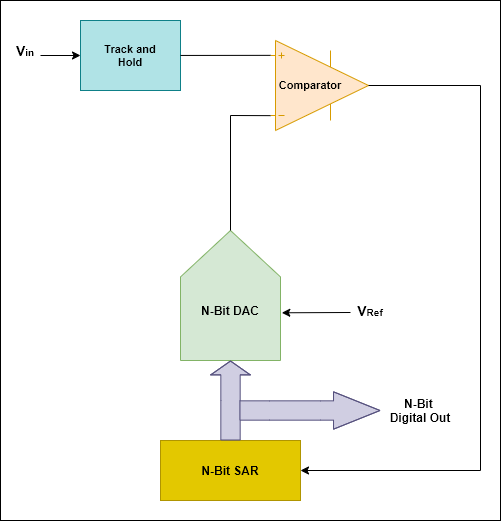
为了直观,看看前文的动图:) [$ S; A" v3 q/ H0 P1 |' R 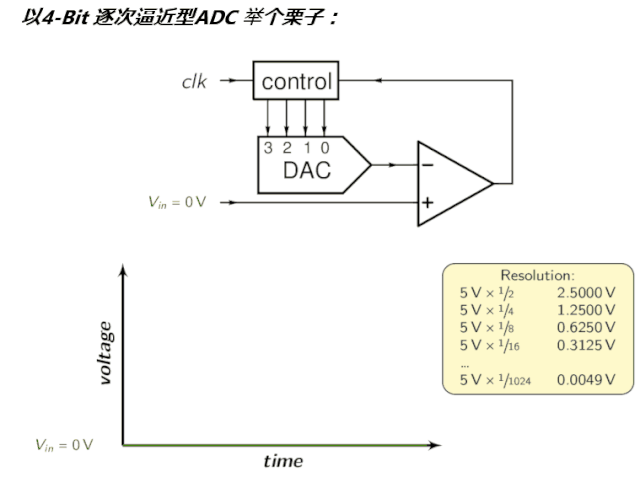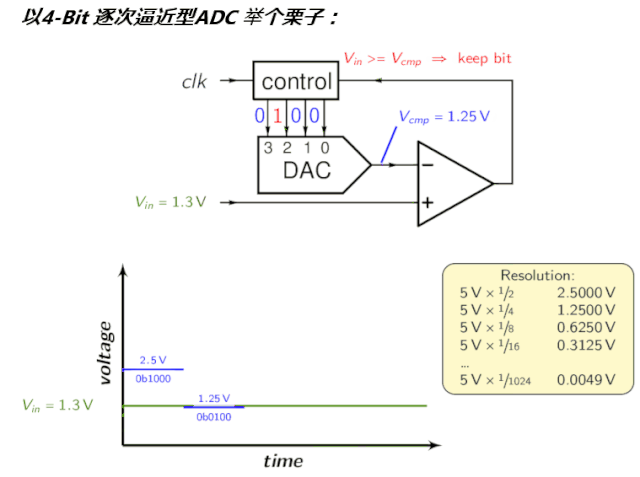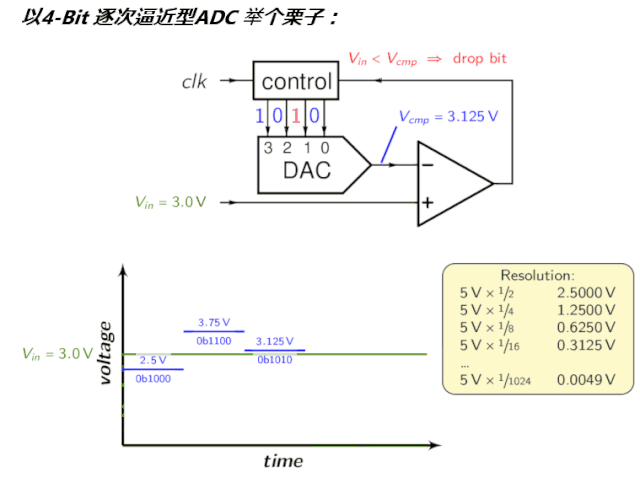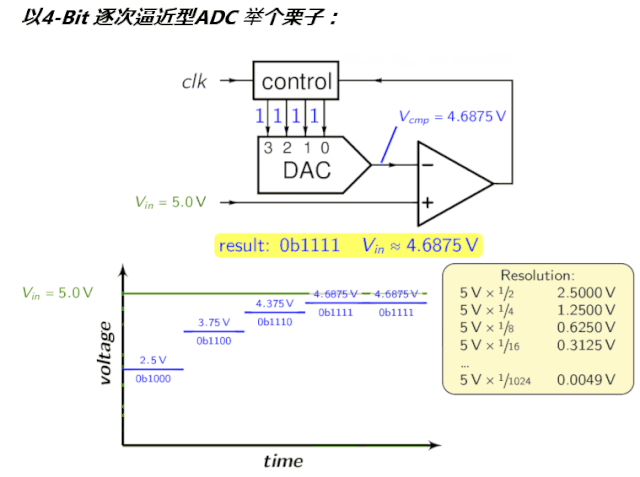
# r" O& W! A2 a Pipelined ADC8 \' O, [, s1 j! b. C" P : x; \+ D7 E2 x) |: X 流水线ADC(也称为子例程量化器)使用两个或多个流水线。首先,进行粗略的转换。第二步,用数模转换器(DAC)确定输入信号的差异。然后将这个差异转换为更细的值,并在最后一步中合并结果。这可以被认为是后续逼近ADC的一种改进,其中反馈参考信号由整个范围的比特(例如,4比特)的中间转换组成,而不仅仅是下一个最重要的比特。结合逐次逼近法和flash adc的优点,该类型具有速度快、分辨率高、模具尺寸小等优点。 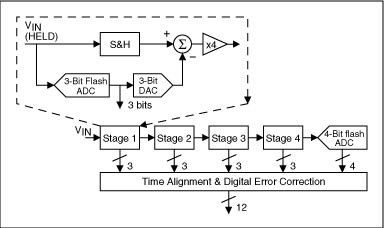
1 d# E3 P& U3 k: S 3 F6 p( H/ z) M& q' r: C: S 在这个原理图中,模拟输入VIN首先被采样并由采样保持器(S&H)保持稳定,而第一阶段的flash ADC将其量化为三位。然后将3位输出馈给3位DAC(精确到12位),然后从输入中减去模拟输出。这个“剩余量”扩大4倍并被送入下一阶段(第二阶段)。这个增加的剩余量继续通过下级流水线,每一阶段提供3位,直到它到达4位flash ADC,将解析最后的4LSB位。因为每个阶段的位是在不同的时间点确定的,所以相同样本对应的所有位在被馈送到数字错误校正逻辑之前都与移位寄存器进行了时间对齐。请注意,当一个流水完成对输入样本的处理,确定本流水采集位并将残差传递到下一个流水时,它便可以开始处理从每个流水中嵌入的采样保持器接收到的下一个样本。这种流水线操作是高吞吐量的原因,这也是流水的概念。先描述一下坑本文来解析一个盆友在使用STM32采集电池电压踩过的坑。以STM32F4 的ADC属于逐次逼近SAR 型ADC为例进行分析,参考STM32F405xx Datasheet,对于如何编写ADC程序就不做描述了。 6 a+ `( y8 M$ S- J4 j 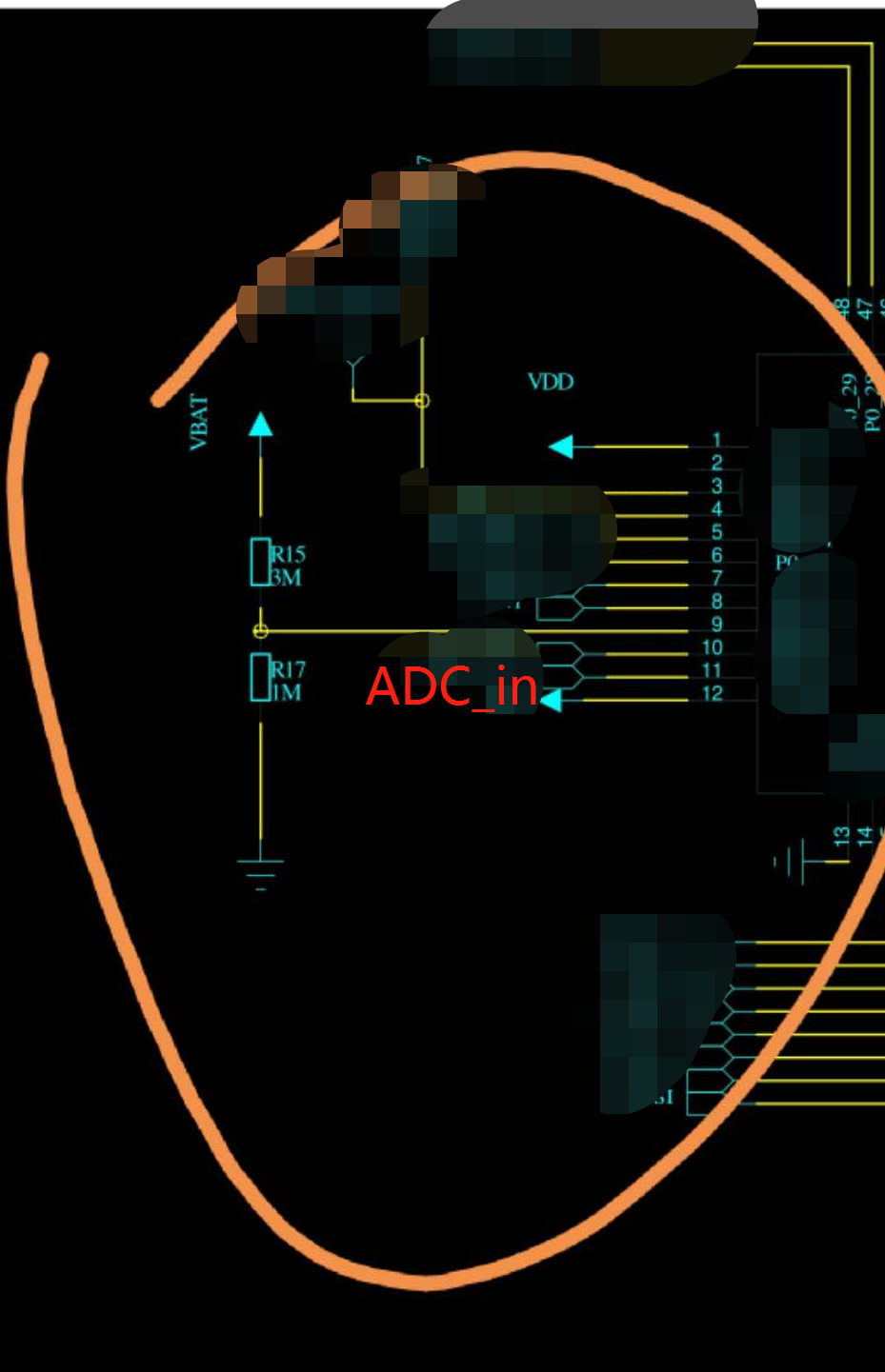
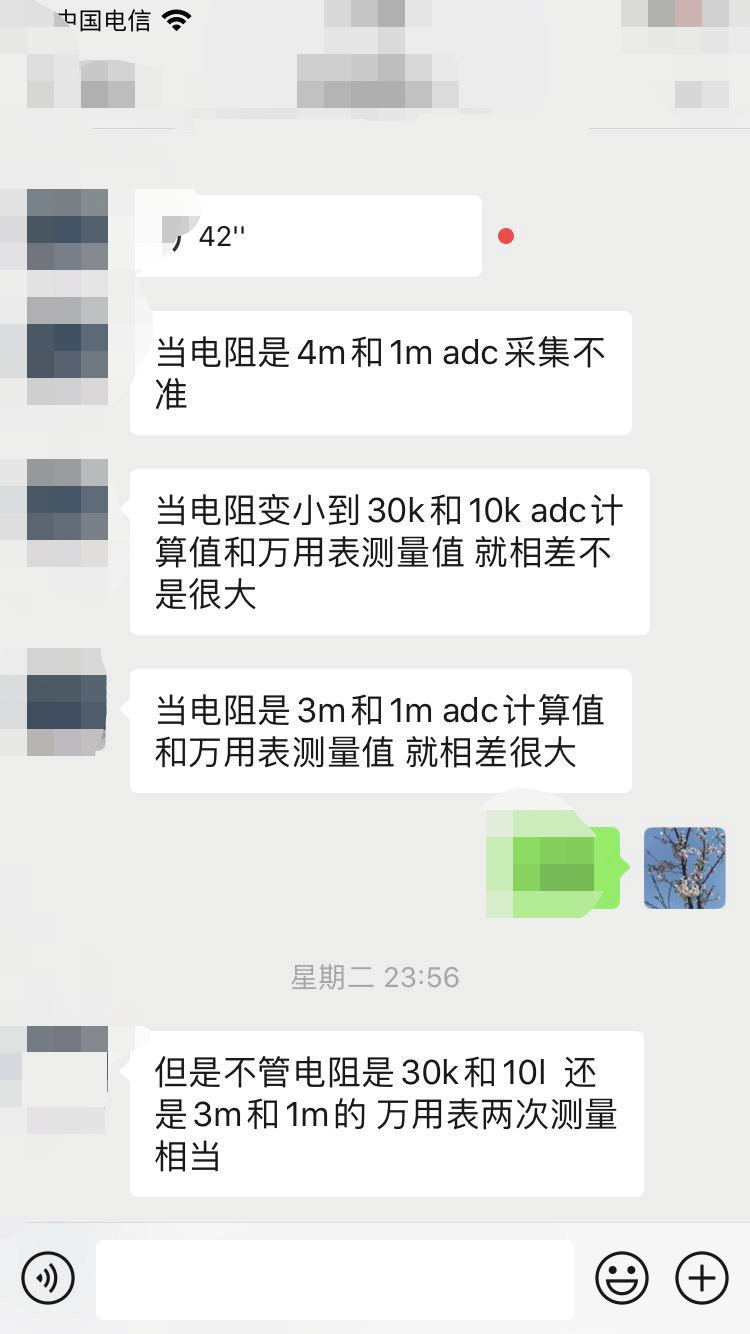
1 N2 a2 w( |, n3 S, g 采集电池电压,利用两个电阻将电池电压分压,然后送入单片机,当电阻如上分别取4M欧/1M欧时,ADC采集到的ADC值与万用表测得的ADC输入端相差很大,取30K欧以及10k欧时,则相差变小。# `4 T& u$ D; Q4 O7 P; a7 H盆友咨询我这是为什么?我给出了建议,先卖个关子,先来看看应用最为广泛的STM32单片机的一些特性。 5 M5 B4 ^% c) y" G STM32 ADC: STM32 12位ADC是逐次逼近型的模数转换器。它有多达19个多路复用通道,允许它测量来自16个外部源、2个内部源和VBAT通道的信号。通道的A/D转换可以在单次、连续、扫描或间断模式下进行。ADC的结果存储在左对齐或右对齐的16位数据寄存器中。模拟看门狗功能允许应用程序检测输入电压是否超过用户定义的、更高或更低的阈值。主要功能,具体操作,怎么编程这些细节,有大量的资料就不罗嗦了,主要来看看电气特性。0 {6 I: C6 D, p' V% @! D . ]" F9 r7 y% o% ]: a- S9 ^% f' b + E: C: p! O }! O5 J 电气特性 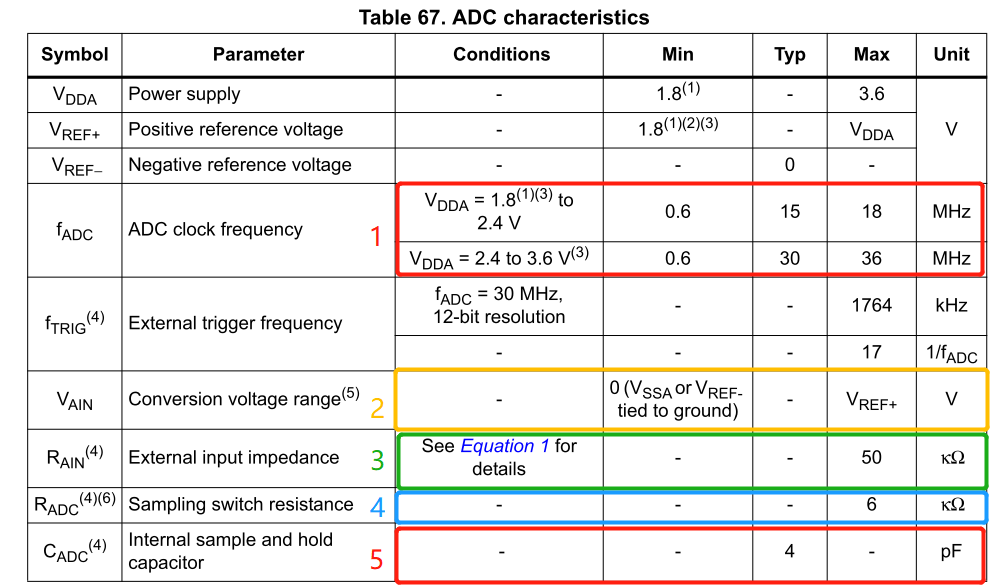

% C6 v# r4 A) D# n. \ 上面的公式用于确定误差小于1/4 LSB时允许的最大外阻抗。N = 12(12位分辨率),k是在ADC_SMPR1寄存器中定义的采样周期数。$ a$ y* y0 p/ ^3 E3 Y) k" D( ^ ADC精度vs.负注入电流:应该避免在任何模拟输入引脚上注入负电流,因为这会显著降低在另一个模拟输入上执行转换的精度。建议在模拟引脚上增加一个肖特基二极管(引脚接地),这可能会注入负电流。 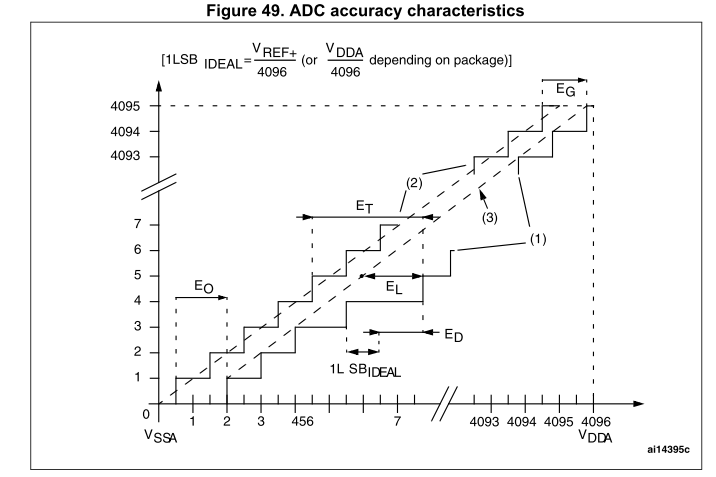
Page 136 图例(上图中标识解释): 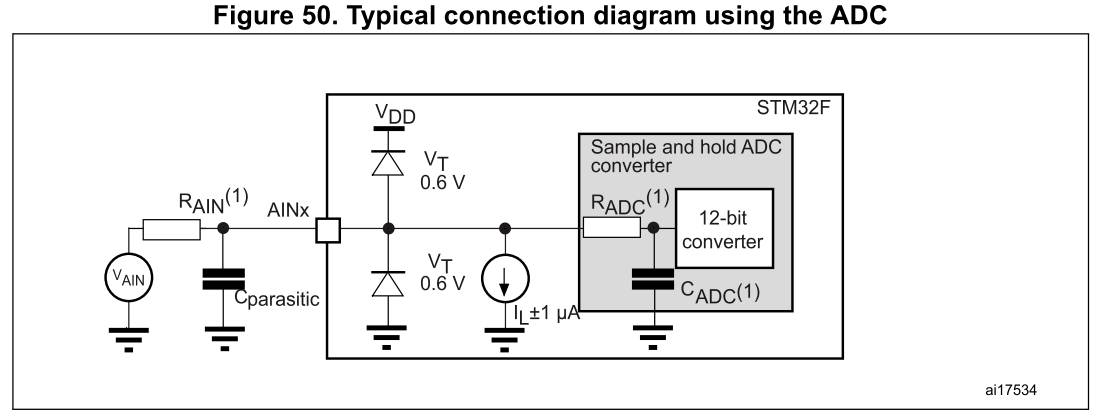
寄生电容表示PCB的电容(取决于焊接和PCB布局质量)加上焊盘电容(大约5 pF)。寄生电容值高会降低转换精度。为了解决这个问题,应该减少fADC。3 A5 r# a: n! V- q回到坑里 将盆友的电路等效绘制一下,忽略ADC采样通道内部ESD保护二极管,以及等效电流源,如下图: 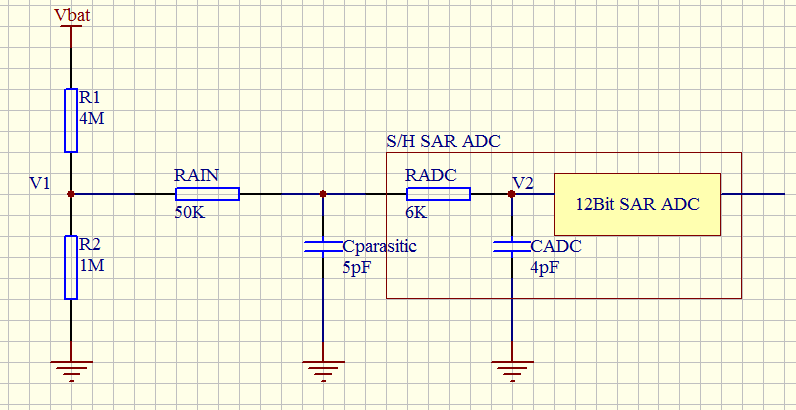
好了,这图一画出来,问题的原因就显而易见了,SAR ADC是将采样电容上的电压通过逐次逼近原理转换为数字量的,按上述图,由于R2为兆级电阻,那么等效加载在采样电容上的电压就不能简单的看成是R1/R2的分压了,此时ADC的输入阻抗在百50K欧级别,简化定性看一下,忽略分布电容影响,计算方便将输入阻抗看成50K直流电阻(实际深入动态分析的话则不可忽略,假定电池电压为5V),具体计算就不做了。为什么电阻选这么大呢?我想估计是为了将电池电压监控取样回路的电流降低,以节省电量。% U7 k2 I/ L/ o; B, S2 y4 d " `9 P4 [7 @% Z: n2 R 跳出坑里 ) o$ `! ] ^- h; j 怎么办呢?我觉得这样应该可以:7 r* ~; j, V8 e& [: [ 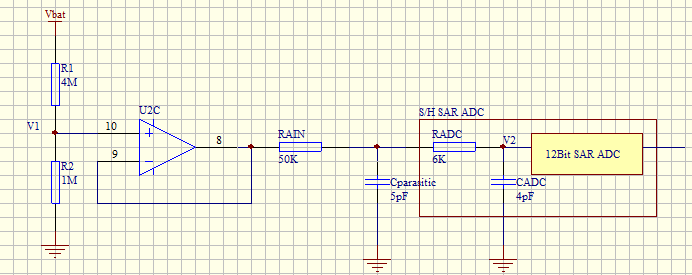
+ {5 ]0 R# j' M* @ 找一个低功耗的运放做一个阻抗变换就可以兼顾两者需求,当然如果更完善一点,还可以考虑串入一个RC低通滤波环节,可以有效降低噪声。 总结一下 在单片机、DSP信号处理系统中,我们免不了要对物理信号进行采样,需要运用到模数转换器件,模数转换器万万千,那么要用好ADC器件,或者使用单片机、DSP内置ADC,了解这些技术指标以及其描述的真实含义,是非常必要的。 熟悉各类ADC的意义,因为如前文所说,嵌入式设备免不了需要采集物理世界的模拟信号。信号各具特点,有的频率高,有的噪声多,有的需要精度高但速度可能不要很快等等。这里整理几种常见ADC(当然还有其他种类比如电荷平衡原理ADC、分时ADC、FM ADC、时间拉伸ADC、增量编码ADC、Wilkinson ADC等等)的原理及特点,了解各类ADC的基本特点,有助于进行器件选型、系统设计。' H0 y5 }$ d, _9 t/ x对于单片机ADC的使用,个人总结了这几点:
|
| 签到 |
| 谢谢分享 |
 微信公众号
微信公众号
 手机版
手机版
