|
一战封神的 0x5f375a86
雷神之锤3是一款九十年代非常经典的游戏,内容画面都相当不错,作者是大名鼎鼎的约翰卡马克。由于当时游戏背景原因,如果想要高效运行游戏优化必须做的非常好,否则普通人的配置性能根本不够用,在这个背景下就诞生了“快速开平方取倒数的算法”。
在早前自雷神之锤3的源码公开后,卡马克大神的代码“一战封神”,令人“匪夷所思”的0x5f375a86 ,引领了一代传奇,源码如下:
- float Q_rsqrt( float number ) {
- long i;
- float x2, y;
- const float threehalfs = 1.5F;
- x2 = number * 0.5F;
- y = number;
- i = * ( long * ) &y;
- // evil floating point bit level hacking
- i = 0x5f3759df - ( i >> 1 ); // what the fuck?
- y = * ( float * ) &i;
- y = y * ( threehalfs - ( x2 * y * y ) );
- // 1st iteration
- // y = y * ( threehalfs - ( x2 * y * y ) );
- // 2nd iteration, this can be removed
- #ifndef Q3_VM
- #ifdef __linux__
- assert( !isnan(y) );
- // bk010122 - FPE?
- #endif
- #endif
- return y; }
相比 sqrt() 函数,这套算法要快将近4倍,要知道,编译器自带的函数,可是经过严格仔细的汇编优化的啊!
牛顿迭代法的原理是先猜测一个值,然后从这个值开始进行叠代。因此,猜测的值越准,叠代的次数越少。卡马克选了0x5f3759df这个值作为猜测的结果,再加上后面的移位算法,得到的y非常接近1/sqrt(n)。这样,我们只需要2次牛顿迭代法就可以达到我们所需要的精度。
函数返回1/sqrt(x),这个函数在图像处理中比sqrt(x)更有用。
注意到这个正数只用了一次叠代!(其实就是根本没用叠代,直接运算)。编译、实验,这个团数不仅工作的很好,而且比标准的sqrt()函数快4倍!
这个简洁的定数,最核心,也是最让人费解的,就是标注了what the fuck的一句 i = 0x5f3759df - ( i >> 1 );再加上y = y * ( threehalfs - ( x2 * y * y ) )。
两句话就完成了开方运算!而且注意到,核心那句是移位运算,速度极快!特别在很多没有乘法指令的RISC结构CPU上,这样做是极其高效的。
算法的原理就是使用牛顿迭代法,用 x-f(x)/f'(x) 来不断的逼近 f(x)=a 的根。
求平方根:f(x)=x^2=a ,f'(x)= 2*x, f(x)/f'(x)=x/2,把 f(x) 代入 x-f(x)/f'(x)后有(x+a/x)/2,
现在我们选 a=5,选一个猜测值比如 2, 那么我们可以这么算 5/2 = 2.5; (2.5+2)/2 = 2.25; 5/2.25 = …… 这样反复迭代下去,结果必定收敛于 sqrt(5)。
但是卡马克作者真正厉害的地方是他选择了一个神秘的常数 0x5f375a86来计算那个梦“值,
就是我们加注释的那一行那行算出的值非常接近1/sqrt(n)这样我们只需要2次牛顿迭代就可以达到我们所需要的精度。
当然目前也已有翻译过C++语言的版本:
- float Q_rsqrt( float number )
- {
- long i;
- float x2, y;
- const float threehalfs = 1.5F;
- x2 = number * 0.5F;
- y = number;
- i = * ( long * ) &y;
- i = 0x5f3759df - ( i >> 1 ); // what the fuck?
- y = * ( float * ) &i;
- y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
- // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
- #ifndef Q3_VM
- #ifdef __linux__
- assert( !isnan(y) ); // bk010122 - FPE?
- #endif
- #endif
- return y;
- }
当然,更加魔幻的是,普渡大学的数学家Chris Lomont看了以后觉得有趣,但也不服气,决定要研究一下卡马克弄出来的这个猜测值有什么奥秘。
在精心研究之后,Lomont从理论上也推导出一个最佳猜测值,和卡马克的数字非常接近, 0x5f37642f。Lomont计算出结果以后非常满意,于是拿自己计算出的起始值和卡马克的神秘数字做比赛,看看谁的数字能够更快更精确的求得平方根。结果是卡马克赢了...
Lomont怒了,采用暴力方法一个数字一个数字试过来,终于找到一个比卡马克数字要好上那么一丁点的数字,虽然实际上这两个数字所产生的结果非常近似,这个暴力得出的数字是0x5f375a86。
囊括世界万物的一段代码
这是一段使用Processing语言的代码,这短短的几行代码永无休止的就在做一件事——“穷举”。那么它又有什么特殊之处吗?
忽略机器本身的性能限制,假设 frameCount 可以无限大(frameCount代表当前帧数)。只需安安静静地盯着屏幕,就可以看到所有像素的所有组合可能。
这意味着你可以在上面看到所有艺术大师的作品,蒙娜丽莎、向日葵甚至是初音……人类历史上所有光辉的瞬间都将闪现在眼前。
但是这又需要多久时间呢?计算机里的每个像素都是由 256 级的 RGB 组成的。因此可以表示 256 ³ (1600万)种颜色。假如图形的分辨率为 1000 × 1000,所有的像素可能的色值相互组合,将会产生 256 的 3000000 次方张不同图片。
如果将图片排在一个长廊上,人以一秒一张的速度去浏览。由于一年有 31536000 秒,因此要走完这条长廊,就需要 10⁷²²⁴⁷¹² 年。
这个数字已经大得很难用人类的常用单位去表示了。硬是要用,那就是 10亿亿亿亿亿亿......年(90万个亿)。要清楚,宇宙的年龄也仅仅是 140 亿年(1.4 × 10¹⁰年)。。
这也意味着,即使你从宇宙大爆炸看到现在,也无法将这个程序看完。但如果把图片像素的精度降低呢?用 100 × 100 的分辨率并且只用黑白二值去表示图形?此时总数就会缩减到 2⁷⁰⁰⁰⁰ ,也就约等于 10³⁰¹⁰。
看似缩小很多了。如果同时动用全人类的力量,将这个任务分配给70亿人。每人还是要不眠不休地看上 3.17 × 10³⁰⁰² 年,才能看完。
即使化到最简,结果仍是大得恐怖。但如果能看完,我手上说不准会有一张 100 × 100 的HelloKitty头像,他手上或许能有一张爱因斯坦吐舌头的照片。
可以用这么简洁的形式去展现万物,用近乎无限的时间去换取无限的可能,我觉得这就是这段代码的魅力所在。
- void setup(){
- size(500,500);
- }
- void draw(){
- for(int i=0;i<width;i++){
- for(int j=0;j<height;j++){
- stroke(frameCount/pow(255,i+j*width)%255,frameCount/pow(255,i+j*width+1)%255,frameCount/pow(255,i+j*width+2)%255);
- point(i,j);
- }
- }
- }
这段代码也有5x5的精简加速版本,当然其中的参数也是可以任意修改的,代码如下:
- int num,w,frame,level;
- void setup(){
- size(400, 400);
- num = 5;
- w = width/num;
- level = 2; //色值精度
- }
- void draw(){
- for(int i = 0; i < num; i++){
- for(int j = 0; j < num; j++){
- fill((int(frame/pow(level,i + j * num)) % level)* (255 / (level - 1)));
- rect(w * i, w * j, w, w);
- }
- }
- // frame++; 匀速播放
- frame = int(pow(frameCount,2)); //加速播放
- }
只有13个字符的Linux Fork炸弹
早在2002年,Jaromil设计了最为精简的一个Linux Fork炸弹,整个代码只有13个字符,在 shell 中运行后几秒后系统就会宕机:
这样看起来不是很好理解,我们可以更改下格式:
更好理解一点的话就是这样:
- bomb()
- {
- bomb|bomb&
- };
- bomb
因为shell中函数可以省略function关键字,所以上面的十三个字符是功能是定义一个函数与调用这个函数,函数的名称为:,主要的核心代码是:|:&,可以看出这是一个函数本身的递归调用,通过&实现在后台开启新进程运行,通过管道实现进程呈几何形式增长,最后再通过:来调用函数引爆炸弹。因此,几秒钟系统就会因为处理不过来太多的进程而死机,解决的唯一办法就是重启。
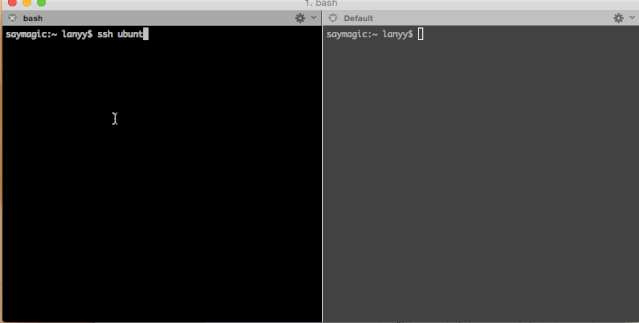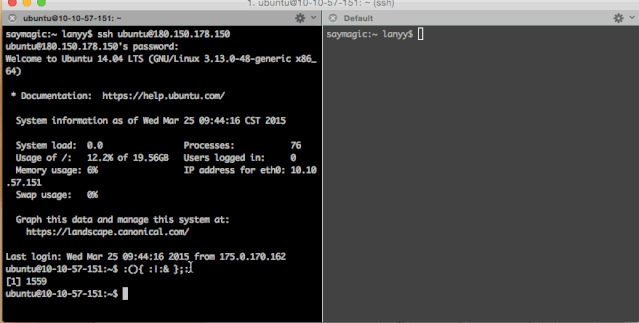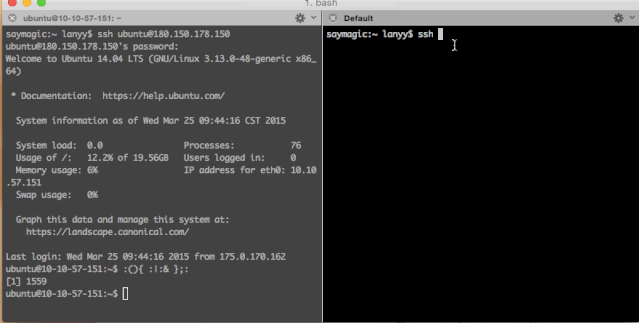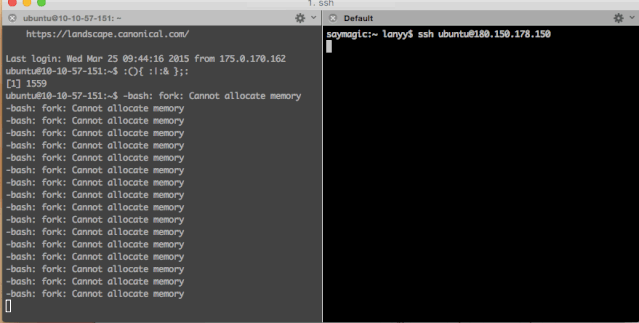
当然有“不怕死”的小伙伴用了云主机试了一试:
结果,运行一段时间后直接报出了-bash: fork: Cannot allocate memory,说明内存不足了。
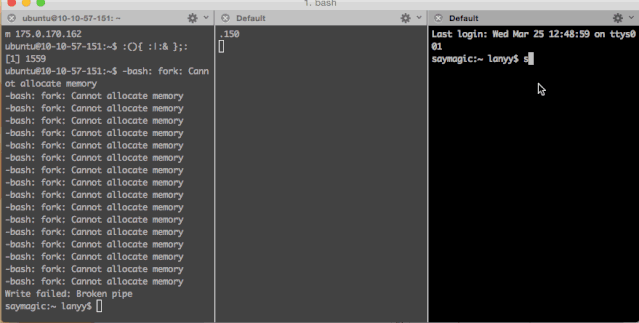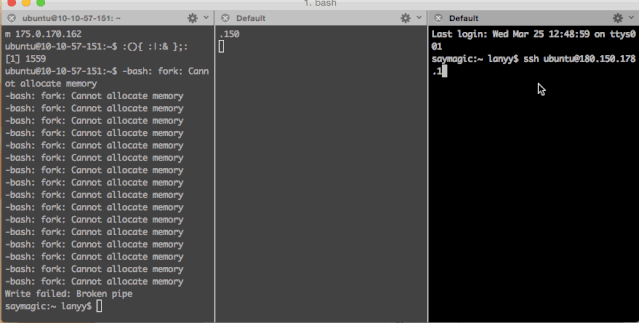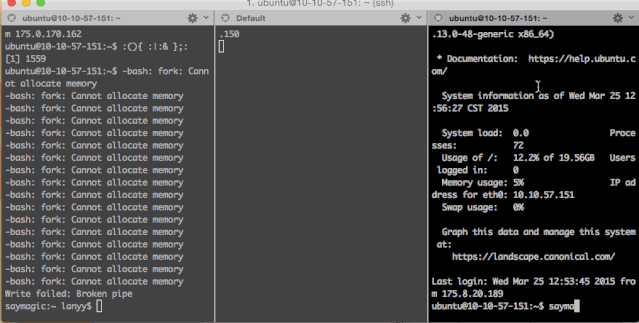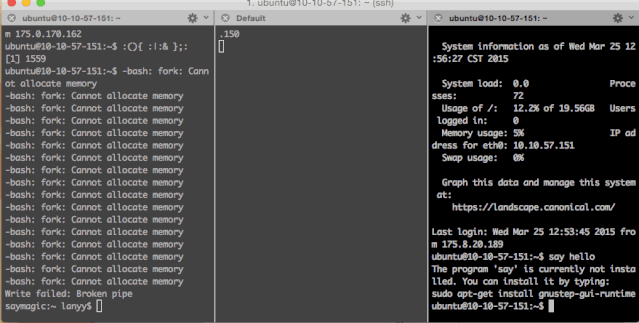
并且在二号终端上尝试连接也没有任何反应。因为是虚拟的云主机,所以我只能通过主机服务商的后台来给主机断电重启。然后才能重新登录:
当然,Fork炸弹用其它语言也可以分分钟写出来一个,例如,python版:
- import os
- while True: os.fork()
- ubuntu@10-10-57-151:~$ ulimit -a
- core file size (blocks, -c) 0
- data seg size (kbytes, -d) unlimited
- scheduling priority (-e) 0
- file size (blocks, -f) unlimited
- pending signals (-i) 7782
- max locked memory (kbytes, -l) 64
- max memory size (kbytes, -m) unlimited
- open files (-n) 1024
- pipe size (512 bytes, -p) 8
- POSIX message queues (bytes, -q) 819200
- real-time priority (-r) 0
- stack size (kbytes, -s) 8192
- cpu time (seconds, -t) unlimited
- max user processes (-u) 7782
- virtual memory (kbytes, -v) unlimited
- file locks (-x) unlimited
可以看到,-u参数可以限制用户创建进程数,因此,我们可以使用ulimit -u 20来允许用户最多创建20个进程。这样就可以预防bomb炸弹。但这样是不彻底的,关闭终端后这个命令就失效了。我们可以通过修改/etc/security/limits.conf文件来进行更深层次的预防,在文件里添加如下一行(ubuntu需更换为你的用户名):
这样,退出后重新登录,就会发现最大进程数已经更改为20了,这个时候我们再次运行炸弹就不会报内存不足了,而是提示-bash: fork: retry: No child processes,说明Linux限制了炸弹创建进程。
东尼·霍尔的快速排序算法
这个算法是由图灵奖得主东尼·霍尔(C. A. R. Hoare)在1960年提出的,从名字中就可以看出,快速就是他的特点。 快速排序采用了“分治法”策略,把一个序列划分为两个子序列。在待排序列中,选择一个元素作为“基准”(Pivot)。
所有小于“基准”的元素,都移动到“基准”前面,所有大于“基准”的元素,都移动到“基准”后面(相同的数可以到任一边)。此为“分区”(partition)操作。
分别对“基准”两边的序列,不断重复一、二步,直至所有子集只剩下一个元素。
假设现有一数列:
对此数列进行快速排序。选择第一个元素 45 作为第一趟排序的“基准”(基准值可以任意选择)。
第一趟:将元素 45 拿出来,分别从数列的两端开始探测
首先从右向左开始,找到第一个小于 45 的元素为 25,然后将 25 放置到第一个元素 45 的位置上。此时数列变为:
然后从左向右开始,找到第一个大于 45 的元素为 66 ,然后将 66 放置到原先元素 25的位置上。此时数列变为:
继续从右向左开始,找到第二个小于 45 的元素为 10 ,然后将 10 放置到原先元素 66的位置上,此时数列变为:
继续从左向右开始,找到第二个大于 45 的元素为 90 ,然后将 90 放置到原先元素 10的位置上,此时数列变为:
继续从右向左开始,此时发现左右碰面,因此将“基准”45 放置到原先元素 90 的位置上,此时数列变为:
至此,第一轮结束,“基准”45 左侧为小数区,右侧为大数区。同样的分别对小数区和大数区应用此方法直至完成排序。
分析完成后通过C++的源代码如下:
快速排序核心算法:
- //每一轮的快速排序
- int QuickPartition (int a[],int low,int high)
- {
- int temp = a[low];//选择数组a的第一个元素作为“基准”
- while(low < high)
- {
- while(low < high && a[high] >= temp )//从右向左查找第一个小于“基准”的数
- {
- high--;
- }
- if (low < high)
- {
- a[low] = a[high];//将第一个找到的大于“基准”的数移动到low处
- low++;
- }
- while(low < high && a[low] <= temp)//从左向右查找第一个大于“基准”的数
- {
- low++;
- }
- if(low < high)
- {
- a[high] = a[low];//将第一个找到的小于“基准”的数移动到high处
- high--;
- }
- a[low] = temp;//将“基准”填到最终位置
- }
- return low;//返回“基准”的位置,用于下一轮排序。
- }
递归调用QuickSort(分治法):
- //快速排序-递归算法
- void QuickSort (int a[],int low,int high)
- {
- if(low < high)
- {
- int temp = QuickPartition(a,low,high);//找出每一趟排序选择的“基准”位置
- QuickSort(a,low,temp-1);//递归调用QuickSort,对“基准”左侧数列排序
- QuickSort(a,temp+1,high);//对“基准”右侧数列排序
- }
- }
主函数调用:
- void main()
- {
- int a[8]={45,38,66,90,88,10,25,45};//初始化数组a
- QuickSort(a,0,7);
- cout<<endl<<"排序后:";
- for(int i = 0;i <= 7;i++)
- {
- cout<<a[i]<<" ";
- }
- getchar();
- }
排序后结果:
毫无炫技又惊为天人的二分图的最大匹配、完美匹配和匈牙利算法
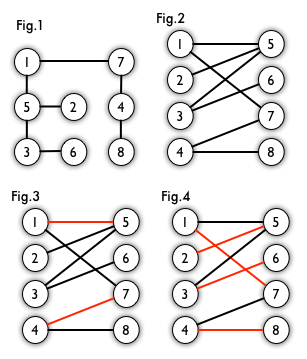
二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交集U和V,使得每一条边都分别连接U、V中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰,我们以后都把它画成图 2 的形式。
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法,下面讲的概念都为这个算法服务。
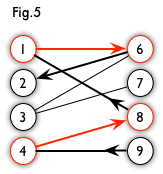
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):
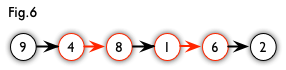
增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前,先讲一下匈牙利树。
匈牙利树一般由 BFS 构造(类似于 BFS 树)。从一个未匹配点出发运行 BFS(唯一的限制是,必须走交替路),直到不能再扩展为止。例如,由图 7,可以得到如图 8 的一棵 BFS 树:
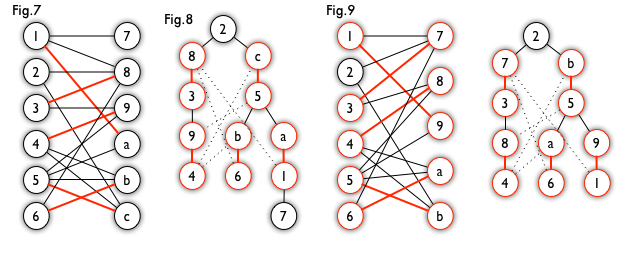
这棵树存在一个叶子节点为非匹配点(7 号),但是匈牙利树要求所有叶子节点均为匹配点,因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点,那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示(顺便说一句,图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路,沿这条增广路扩充后将得到一个完美匹配)。
下面给出匈牙利算法的 DFS 和 BFS 版本的代码:
- // 顶点、边的编号均从 0 开始
- // 邻接表储存
- struct Edge
- {
- int from;
- int to;
- int weight;
- Edge(int f, int t, int w):from(f), to(t), weight(w) {}
- };
- vector<int> G[__maxNodes]; /* G[i] 存储顶点 i 出发的边的编号 */
- vector<Edge> edges;
- typedef vector<int>::iterator iterator_t;
- int num_nodes;
- int num_left;
- int num_right;
- int num_edges;
- int matching[__maxNodes]; /* 存储求解结果 */
- int check[__maxNodes];
- bool dfs(int u)
- {
- for (iterator_t i = G[u].begin(); i != G[u].end(); ++i) { // 对 u 的每个邻接点
- int v = edges[*i].to;
- if (!check[v]) { // 要求不在交替路中
- check[v] = true; // 放入交替路
- if (matching[v] == -1 || dfs(matching[v])) {
- // 如果是未盖点,说明交替路为增广路,则交换路径,并返回成功
- matching[v] = u;
- matching[u] = v;
- return true;
- }
- }
- }
- return false; // 不存在增广路,返回失败
- }
- int hungarian()
- {
- int ans = 0;
- memset(matching, -1, sizeof(matching));
- for (int u=0; u < num_left; ++u) {
- if (matching[u] == -1) {
- memset(check, 0, sizeof(check));
- if (dfs(u))
- ++ans;
- }
- }
- return ans;
- }<u></u>
- queue<int> Q;
- int prev[__maxNodes];
- int Hungarian()
- {
- int ans = 0;
- memset(matching, -1, sizeof(matching));
- memset(check, -1, sizeof(check));
- for (int i=0; i<num_left; ++i) {
- if (matching[i] == -1) {
- while (!Q.empty()) Q.pop();
- Q.push(i);
- prev[i] = -1; // 设 i 为路径起点
- bool flag = false; // 尚未找到增广路
- while (!Q.empty() && !flag) {
- int u = Q.front();
- for (iterator_t ix = G[u].begin(); ix != G[u].end() && !flag; ++ix) {
- int v = edges[*ix].to;
- if (check[v] != i) {
- check[v] = i;
- Q.push(matching[v]);
- if (matching[v] >= 0) { // 此点为匹配点
- prev[matching[v]] = u;
- } else { // 找到未匹配点,交替路变为增广路
- flag = true;
- int d=u, e=v;
- while (d != -1) {
- int t = matching[d];
- matching[d] = e;
- matching[e] = d;
- d = prev[d];
- e = t;
- }
- }
- }
- }
- Q.pop();
- }
- if (matching[i] != -1) ++ans;
- }
- }
- return ans;
- }
匈牙利算法的要点如下
- 从左边第 1 个顶点开始,挑选未匹配点进行搜索,寻找增广路。
- 如果经过一个未匹配点,说明寻找成功。更新路径信息,匹配边数 +1,停止搜索。
- 如果一直没有找到增广路,则不再从这个点开始搜索。事实上,此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去,而不影响结果。
- 由于找到增广路之后需要沿着路径更新匹配,所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈,而 BFS 版本使用 prev 数组。
性能比较
两个版本的时间复杂度均为O(V·E)。DFS 的优点是思路清晰、代码量少,但是性能不如 BFS。我测试了两种算法的性能。对于稀疏图,BFS 版本明显快于 DFS 版本;而对于稠密图两者则不相上下。在完全随机数据 9000 个顶点 4,0000 条边时前者领先后者大约 97.6%,9000 个顶点 100,0000 条边时前者领先后者 8.6%, 而达到 500,0000 条边时 BFS 仅领先 0.85%。补充定义和定理:
最大匹配数:最大匹配的匹配边的数目
最小点覆盖数:选取最少的点,使任意一条边至少有一个端点被选择
最大独立数:选取最多的点,使任意所选两点均不相连
最小路径覆盖数:对于一个 DAG(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 0(即单个点)。
定理1:最大匹配数 = 最小点覆盖数(这是 Konig 定理)定理2:最大匹配数 = 最大独立数定理3:最小路径覆盖数 = 顶点数 - 最大匹配数
|

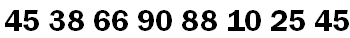
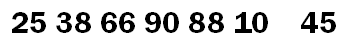
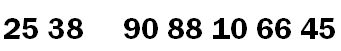
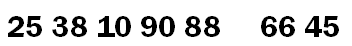
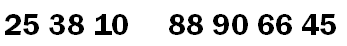






 微信公众号
微信公众号
 手机版
手机版
