
|
1 前言 Q格式是二进制的定点数格式,相对于浮点数,Q格式指定了相应的小数位数和整数位数,在没有浮点运算的平台上,可以更快地对浮点数据进行处理,以及应用在需要恒定分辨率的程序中(浮点数的精度是会变化的);需要注意的是Q格式是概念上小数定点,通过选择常规的二进制数整数位数和小数位数,从而达到所需要的数值范围和精度,这里可能有点抽象,下面继续看介绍。 2 Q数据的表示2.1 范围和精度定点数通常表示为,其中m为整数个数,n为小数个数,其中最高位位符号位并且以二进制补码的形式存储;
无符号的用
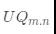
无符号Q格式数据的推导
这里以一个16位无符号整数为例, 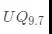

所以不难看出, 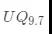
根据等比数列求和公式得到,整数域最大值如下: 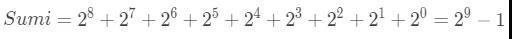
小数域最大值如下: 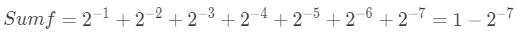
因此
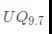
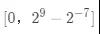
有符号Q格式数据的推导
这里以一个16位有符号整数为例, 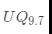

0 N+ g' P( L0 `! B( {/ `/ N g! ]7 B 所以不难求出, 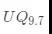
根据等比数列求和公式得到,整数域最大值如下: 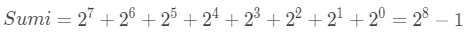
小数域最大值如下: 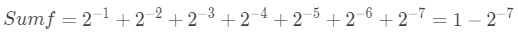
. {! o4 D7 q0 A+ [% q$ _0 J 因此最大能表示的数为:
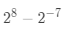
所能表示的最小数据的二进制形式如下图所示;

可以从图中看到,该数表示为;
综上,可以得到有符号的范围是:
3 Q数据的运算3.1 0x7FFF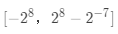
最大数的十六进制为0x7FFF,如下图所示;

3.2 0x8000 最小数的十六进制为0X8000,如下图所示;

上述这两种情况,下面都会用到。 1 j% C. Q- [. }- ]/ }; n 3.3 加法加法和减法需要两个Q格式的数据定标相同,即
int16_t q_add(int16_t a, int16_t b)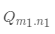
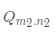
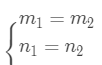
{ return a + b;( y9 T- z @; ]4 } }: [* D8 ^5 X: W) i- l( L 上面的程序其实并不安全,在一般的DSP芯片具有防止溢出的指令,但是通常需要做一下溢出检测,具体如下所示; //http://great.blog.csdn.net/1 y' s! D) b0 Z; i6 ?# b' Iint16_t q_add_sat(int16_t a, int16_t b) {3 `: E3 X* O2 F int16_t result; int32_t tmp;- s" R6 E- f% }- [0 ]6 p tmp = (int32_t)a + (int32_t)b; if (tmp > 0x7FFF)& V" Q' Z3 S1 R! S tmp = 0x7FFF; if (tmp < -1 * 0x8000) tmp = -1 * 0x8000; result = (int16_t)tmp; return result;# f4 N1 ~# \/ J: |0 q4 A7 P }9 c0 ~; }; z3 W9 P2 k 3.4 减法 类似于加法的操作,需要相同定标的两个Q格式数进行相减,但是不会存在溢出的情况; //http://great.blog.csdn.net/int16_t q_sub(int16_t a, int16_t b) { return a - b;6 C% y1 p7 D5 l9 D3 K( M* F }- ^0 c0 V2 m% e, a) I' D- L 3.5 乘法 乘法同样需要考虑溢出的问题,这里通过sat16函数,对溢出做了处理; //http://great.blog.csdn.net/, b5 ]4 j: o% R s// precomputed value:, s5 E9 X6 o6 @7 q5 s* L% n# ` #define K (1 << (Q - 1)) // saturate to range of int16_t& @. _' N2 s: O4 p6 _6 J int16_t sat16(int32_t x) { if (x > 0x7FFF) return 0x7FFF; else if (x < -0x8000) return -0x8000;0 X2 \# b6 p! P. ]# k; r5 b! H; e v else return (int16_t)x; }7 |9 R, ~& a4 z5 U) H- d( D int16_t q_mul(int16_t a, int16_t b)+ F: K4 J& G( w/ U' o; j {" N+ D5 I$ `9 t2 }7 s int16_t result;& |' g+ `: A1 g. J4 ^1 w int32_t temp;+ U0 j5 b. C# b1 p2 P temp = (int32_t)a * (int32_t)b; // result type is operand's type // Rounding; mid values are rounded up temp += K; // Correct by dividing by base and saturate result2 h- h+ F7 C1 d9 Y) [ result = sat16(temp >> Q); return result;5 Z" V. r! c4 l- h% V: a } 3.6 除法//http://great.blog.csdn.net/2 k6 j5 k4 j0 V% S+ H int16_t q_div(int16_t a, int16_t b)3 s9 V% R( ?: e0 Y% ^/ J/ R& _ { R- A, J5 s$ M/ r( U /* pre-multiply by the base (Upscale to Q16 so that the result will be in Q8 format) */2 r/ T( _. J. l9 C int32_t temp = (int32_t)a << Q;: [, f1 H3 _ o+ T0 d9 h /* Rounding: mid values are rounded up (down for negative values). */8 p7 T6 Q1 C' |) b; D /* OR compare most significant bits i.e. if (((temp >> 31) & 1) == ((b >> 15) & 1)) */5 }. C9 t+ h5 _. ~* h) Z if ((temp >= 0 && b >= 0) || (temp < 0 && b < 0)) { temp += b / 2; /* OR shift 1 bit i.e. temp += (b >> 1); */ } else {, j" Q% |/ x" m* k+ k$ w) ? temp -= b / 2; /* OR shift 1 bit i.e. temp -= (b >> 1); */# ?% x- D5 f7 G8 v: g& E }9 \; r# f* \, [; g& s) d return (int16_t)(temp / b); }' H& V5 A3 X% i/ e/ T1 C+ m& M 4 常见Q格式的数据范围 定点数和浮点数转换的关系满足以下公式: 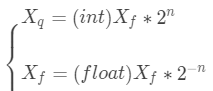
#include <stdio.h>( ^: ?1 T# }; b+ Z5 Q/ M7 W5 ] #include <stdint.h> #include <math.h> ! e* k8 _2 h. U- ^ int main()6 G* }1 y/ }" U" U/ ^ {9 W6 c: H4 k6 P" {$ t6 Y! z/ \6 S# ? // 0111 1111 1111 1111 int16_t q_max = 32767; // 0x7FFF x" S. D& \- b d // 1000 0000 0000 0000 int16_t q_min = -32768; // 0x8000 float f_max = 0; float f_min = 0;/ O: c3 \2 F8 K* q: a8 r printf("\r\n"); for (int8_t i = 15; i>=0; i--) { f_max = (float)q_max / pow(2,i); f_min = (float)q_min / pow(2,i); _+ S1 E2 @' j" R" s( s- @ printf("\t| Q %d | Q %d.%d| %f | %f |\r\n", i,(15-i),i,f_max,f_min); }+ l7 e% }& {5 W2 f V return 0; } 运行得到结果如下所示;

- K0 ?) o& S7 F+ J* h Q 格式 Qmn Max Min Q 15Q 0.150.999969-1.0000008 P$ @ O* e; b/ k8 g Q 14Q 1.141.999939-2.000000 Q 13Q 2.133.999878-4.000000! V; w/ I1 I& T3 s Q 12Q 3.127.999756-8.000000 Q 11Q 4.1115.999512-16.000000 F2 D" o. W1 a9 w$ W/ z# Z; l Q 10Q 5.1031.999023-32.000000 Q 9Q 6.963.998047-64.000000* L! Q4 R5 f3 Y/ A8 }( v; Z Q 8Q 7.8127.996094-128.0000005 G: H* M6 E9 u6 }: A. C Q 7Q 8.7255.992188-256.0000007 h7 S; P& c6 [6 t; h# o# I: K Q 6Q 9.6511.984375-512.000000 Q 5Q 10.51023.968750-1024.000000' j$ |9 o6 l7 }5 ^9 G) w2 I Q 4Q 11.42047.937500-2048.0000000 |( H6 g3 a3 m, i* X' ^$ V Q 3Q 12.34095.875000-4096.000000 Q 2Q 13.28191.750000-8192.0000005 H- z: [6 O5 c6 d- e Q 1Q 14.116383.500000-16384.000000 Q 0Q 15.032767.000000-32768.0000005 0x5f3759df Q格式虽然十分抽象,但是且看看这个数字0x5f3759df,感觉和Q格式有某种联系,它是雷神之锤3中的一个算法的魔数,毕竟游戏引擎需要充分考虑到效率,具体的由来可以看一下论文《Fast Inverse Square Root》,下面是源码中剥出来的快速平方根算法; float Q_rsqrt( float number ){( e/ U" D( C, M long i;* T, G' e$ T7 _9 F- z float x2, y; const float threehalfs = 1.5F; * g! e; h4 p' u9 n1 n8 T. r x2 = number * 0.5F; y = number;4 K; M& C9 l: j) {' F9 O, I i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i;7 Q; `" M6 k' f2 Y y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed #ifndef Q3_VM4 I) Q: x* N; W7 U3 d! K0 \4 k #ifdef __linux__ assert( !isnan(y) ); // bk010122 - FPE? #endif #endif return y; } 6 总结 本文介绍了Q格式的表示方式以及相应的运算,另外需要注意在Q格式运算的时候,两者定标必须相同,对于数据的溢出检测也要做相应的处理。 |
 微信公众号
微信公众号
 手机版
手机版
