浮点型精度相关问题

[复制链接]

gaosmile 发布时间：2020-7-21 20:12

技术帖
文章封面:	-
文章简介:	-

1 引言

先举个例子：

#include <stdio.h>

int main()
{
float a = 0.1;
float b = 0.2;
float c = a + b;

if(c == 0.3){
printf("c == 0.3\n");
}else{
printf("0.1 + 0.2 != 0.3\n");
}
return 0;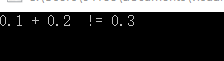
}
å¾®ä¿¡å¾ç_20200721201029.png

c != 0.3

a,b,c局部变量值

如果变量 a , b 换 0.75 ， 0.5 可以看出运行出 c == 1.25 ,说明浮点数运算是不稳定的。

a=0.5,b=0.75,c == 1.25

为什么会时好时坏，因为不是所有的小数能用浮点数标准 ( IEEE 754 ) 表示出来。

所以，判断两个浮点数变量是否相等，不能简单地通过 "==" 运算符实现，浮点数进行比较时，一般比较他们之间的差值在一定范围之内。

bool feq(float a,float b){
return fabs(a,b)<FLT_EPSILON;
}

FLT_EPSILON 数值是 1.192092896e-07F,最小的 float 型数，它使 1.0+FLT_EPSILON !=1.0

2 为什么浮点数精度会丢失

十进制小数转化为二进制数：乘以2直到没有了小数为止。

举个例子，0.9 表示成二进制数。

0.9*2=1.8 取整数部分 1
0.8(1.8的小数部分)*2=1.6 取整数部分 1
0.6*2=1.2 取整数部分 1
0.2*2=0.4 取整数部分 0
0.4*2=0.8 取整数部分 0
0.8*2=1.6 取整数部分 1
0.6*2=1.2 取整数部分 0
.........
0.9二进制表示为(从上往下): 1100100100100......

很显然，小数的二进制表示有时是不可能精确的。其实道理很简单，十进制系统中能不能准确表示出 2/3 呢？同样二进制系统也无法准确表示 1/10 。这也就解释了为什么浮点型精度丢失问题。

3 float 存储原理

float 型在内存中占 4 个字节。float 的 32 个二进制位结构如下：

float 内存存储结构

[td]

31	30	29----23	22----0
实数符号位	指数符号位	指数位	有效数位

其中符号位 1 表示正，0 表示负。有效位数位 24 位，其中一位是实数符号位。

将一个 float 型转化为内存存储格式的步骤为：

先将这个实数的绝对值化为二进制格式，注意实数的整数部分和小数部分的二进制方法在上面已经探讨过了。
将这个二进制格式实数的小数点左移或右移 n 位，直到小数点移动到第一个有效数字的右边。
从小数点右边第一位开始数出二十三位数字放入第 22 到第 0 位。
如果实数是正的，则在第 31 位放入“0”，否则放入“1”。
如果是左移得到的，说明指数是正的，第 30 位放入“1”。如果 n 是右移得到的或 n=0，则第 30 位放入“0”。
如果 n 是左移得到的，则将 n 减去 1 后化为二进制，并在左边加“0”补足七位，放入第 29 到第 23 位。如果n是右移得到的或 n=0，则将 n 化为二进制后在左边加“0”补足七位，再各位求反，再放入第 29 到第 23 位。
$ \" O R% M0 ]5 h y

0.2356 的内存存储格式：