无刷电机属于自换流型（自我方向转换），因此控制起来更加复杂。

- a$ k1 d6 ]# b, X2 `BLDC电机控制要求了解电机进行整流转向的转子位置和机制。对于闭环速度控制，有两个附加要求，即对于转子速度或电机电流以及PWM信号进行测量，以控制电机速度以及功率。
; r- V1 X7 B7 @- J$ Z
# {- a1 \. M; hBLDC电机可以根据应用要求采用边排列或中心排列PWM信号。大多数应用仅要求速度变化操作，将采用6个独立的边排列PWM信号。这就提供了最高的分辨率。如果应用要求服务器定位、能耗制动或动力倒转，推荐使用补充的中心排列PWM信号。
! U8 K" f% |0 \. U( J% E0 U" P, M
4 g( h. ]2 J$ I为了感应转子位置，BLDC电机采用霍尔效应传感器来提供绝对定位感应。这就导致了更多线的使用和更高的成本。无传感器BLDC控制省去了对于霍尔传感器的需要，而是采用电机的反电动势（电动势）来预测转子位置。无传感器控制对于像风扇和泵这样的低成本变速应用至关重要。在采用 BLDC 电机时，冰箱和空调压缩机也需要无传感器控制。

空载时间的插入和补充：

大多数BLDC电机不需要互补的PWM、空载时间插入或空载时间补偿。可能会要求这些特性的BLDC应用仅为高性能BLDC伺服电动机、正弦波激励式BLDC电机、无刷AC、或PC同步电机。

控制算法许多不同的控制算法都被用以提供对于BLDC电机的控制。典型做法是，将功率晶体管用作线性稳压器来控制电机电压。当驱动高功率电机时，这种方法并不实用。高功率电机必须采用PWM控制，并要求一个微控制器来提供起动和控制功能。
9 F% A# R# Z( o/ I6 D
5 K8 D' c. Q5 r% a  [控制算法必须提供下列三项功能：
▪ 用于控制电机速度的 PWM 电压;
▪ 用于对电机进整流换向的机制;
▪ 利用反电动势或霍尔传感器来预测转子位置的方法;

脉冲宽度调制仅用于将可变电压应用到电机绕组。有效电压与PWM占空比成正比。当得到适当的整流换向时，BLDC的扭矩速度特性与以下直流电机相同。可以用可变电压来控制电机的速度和可变转矩。

图1

5 R  A5 D$ `7 v% P

功率晶体管的换向实现了定子中的适当绕组可根据转子位置生成最佳的转矩。在一个BLDC电机中，MCU必须知道转子的位置并能够在恰当的时间进行整流换向。
2 Y" s4 W0 d" Z+ J- T
. m+ Q& D5 `0 l; Q4 TBLDC电机的梯形整流换向，对于直流无刷电机采用所谓的梯形整流换向是最简单的方法之一。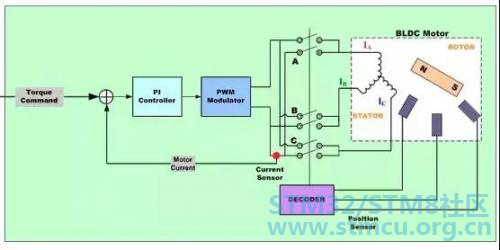

/ f; \, M" N/ S* j6 z( d+ y

图2：用于BLDC电机的梯形控制器的简化框图
" f% f4 L9 S3 `( t& b

在图 2 中，每一次要通过一对电机终端来控制电流，而第三个电机终端总是与电源电学上断开。

嵌入大电机中的三种霍尔器件用于提供数字信号，它们在60度的扇形区内测量转子位置，并在电机控制器上提供这些信息。由于每次两个绕组上的电流量相等，而第三个绕组上的电流为零，这种方法仅能产生具有六个方向其中之一的电流空间矢量。随着电机的转动，电机终端的电流在每转 60 度时，实现一次电开关（整流换向），因此电流空间矢量总是在 90 度相移的最接近 30 度的位置。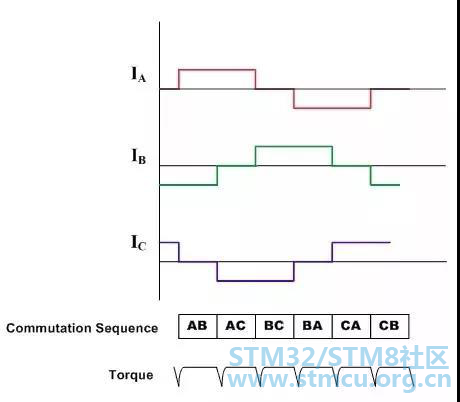

图3：梯形控制：驱动波形和整流处的转矩

& v8 \; Y, |5 v因此每个绕组的电流波型为梯形，从零开始到正电流再到零然后再到负电流。

9 m7 h: a3 }3 {0 h; z( v, Q这就产生了电流空间矢量，当它随着转子的旋转在 6 个不同的方向上进行步升时，它将接近平衡旋转。

在像空调和冰箱这样的电机应用中，采用霍尔传感器并不是一个不变的选择。在非联绕组中感应的反电动势传感器可以用来取得相同的结果。

这种梯形驱动系统因其控制电路的简易性而非常普通，但是它们在整流过程中却要遭遇转矩纹波问题。

4 n5 Q3 H& ~& {4 R, C; z- ~

BLDC电机的正弦整流换向梯形整流换向还不足以为提供平衡、精准的无刷直流电机控制。这主要是因为在一个三相无刷电机（带有一个正统波反电动势）中所产生的转矩由下列等式来定义：
) m  s! w  w+ ]1 T7 a+ P
; n8 }, b) x3 r3 p$ y  S, e2 N转轴转矩=Kt [IRSin（o）+ISSin（o+120）+ITSin（o+240）]

4 w; ], c: H+ [$ t, l其中：
o 为转轴的电角度
Kt 为电机的转矩常数
/ a% L9 ]/ ?+ `- h: DIR，IS 和 IT 为相位电流

如果相位电流是正弦的：IR=I0Sino；IS=I0Sin（+120o）；IT=I0Sin（+240o）
+ s) L! q, N! H( q

将得到：转轴转矩=1.5I0*Kt（一个独立于转轴角度的常数）
8 V: \$ @8 m9 g0 Y/ E# y! U7 V
3 _! D5 h! s1 ?1 J4 }/ z正弦整流换向无刷电机控制器努力驱动三个电机绕组，其三路电流随着电机转动而平稳的进行正弦变化。选择这些电流的相关相位，这样它们将会产生平稳的转子电流空间矢量，方向是与转子正交的方向，并具有不变量。这就消除了与转向相关的转矩纹波和转向脉冲。
+ k  t8 ]& Z4 o! n6 f0 b
为了随着电机的旋转，生成电机电流的平稳的正弦波调制，就要求对于转子位置有一个精确有测量。霍尔器件仅提供了对于转子位置的粗略计算，还不足以达到目的要求。基于这个原因，就要求从编码器或相似器件发出角反馈。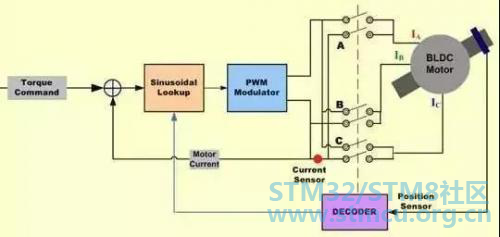

图4：BLDC 电机正弦波控制器的简化框图

由于绕组电流必须结合产生一个平稳的常量转子电流空间矢量，而且定子绕组的每个定位相距 120 度角，因此每个线组的电流必须是正弦的而且相移为 120 度。采用编码器中的位置信息来对两个正弦波进行合成，两个间的相移为 120 度。然后，将这些信号乘以转矩值，因此正弦波的振幅与所需要的转矩成正比。结果，两个正弦波电流命令得到恰当的定相，从而在正交方向产生转动定子电流空间矢量。
/ P! l% x3 ~9 K+ t; @0 L
正弦电流命令信号输出一对在两个适当的电机绕组中调制电流的P-I控制器。第三个转子绕组中的电流是受控绕组电流的负数和，因此不能被分别控制。每个P-I控制器的输出被送到一个PWM调制器，然后送到输出桥和两个电机终端。应用到第三个电机终端的电压源于应用到前两个线组的信号的负数和，用于分别间隔 120 度的三个正弦电压。

6 m$ ]; t: q. x5 w% V+ P# Y5 O) X结果，实际输出电流波形精确的跟踪正弦电流命令信号，所得电流空间矢量平稳转动，在量上得以稳定并以所需的方向定位。
3 V3 B' b7 E0 Q/ ^3 n: `6 A- O7 P, z
* b- l; p# i( t" M) S0 E# d一般通过梯形整流转向，不能达到稳定控制的正弦整流转向结果。然而，由于其在低电机速度下效率很高，在高电机速度下将会分开。这是由于速度提高，电流回流控制器必须跟踪一个增加频率的正弦信号。同时，它们必须克服随着速度提高在振幅和频率下增加的电机的反电动势。
4 e# m- r1 A) G

0 T" q3 v; ^2 L- }7 T% j! X

由于P-I控制器具有有限增益和频率响应，对于电流控制回路的时间变量干扰将引起相位滞后和电机电流中的增益误差，速度越高，误差越大。这将干扰电流空间矢量相对于转子的方向，从而引起与正交方向产生位移。
7 V# j1 Q9 Q" `
当产生这种情况时，通过一定量的电流可以产生较小的转矩，因此需要更多的电流来保持转矩，效率降低。

2 E1 p; d: w- n+ S随着速度的增加，这种降低将会延续。在某种程度上，电流的相位位移超过 90 度。当产生这种情况时，转矩减至为零。通过正弦的结合，上面这点的速度导致了负转矩，因此也就无法实现。
3 h/ Y1 i$ V# G& q* G$ F$ a& K/ }
' G% i2 F5 S- v5 D! ?

AC 电机控制算法

01

标量控制

4 z' w6 U: n, n7 z1 U

标量控制（或 V/Hz 控制）是一个控制指令电机速度的简单方法。指令电机的稳态模型主要用于获得技术，因此瞬态性能是不可能实现的。系统不具有电流回路。为了控制电机，三相电源只有在振幅和频率上变化。
) }  y, h5 M! r; G! ^( s
' P9 m8 k1 U1 X0 \) }0 q& T

02

矢量控制或磁场定向控制

在电动机中的转矩随着定子和转子磁场的功能而变化，并且当两个磁场互相正交时达到峰值。在基于标量的控制中，两个磁场间的角度显著变化。
4 C4 g0 N" W$ U/ Z1 E  V& D. {/ J
矢量控制设法在 AC 电机中再次创造正交关系。为了控制转矩，各自从产生的磁通量中生成电流，以实现 DC 机器的响应性。
; X2 d+ }6 e; B5 w- A
一个 AC 指令电机的矢量控制与一个单独的励磁 DC 电机控制相似。在一个 DC 电机中，由励磁电流 IF 所产生的磁场能量ΦF 与由电枢电流 IA 所产生的电枢磁通ΦA 正交。这些磁场都经过去耦并且相互间很稳定。因此，当电枢电流受控以控制转矩时，磁场能量仍保持不受影响，并实现了更快的瞬态响应。
0 L1 E8 ~0 E# T% }$ O; H
2 W" O! A+ }1 B' j$ M3 Q2 p三相 AC 电机的磁场定向控制（FOC）包括模仿 DC 电机的操作。所有受控变量都通过数学变换，被转换到 DC 而非 AC。其目标是独立的控制转矩和磁通。
9 J; ~( G0 D7 Y/ }, w

; {$ T( g5 R1 B: x  V5 B% u( i; P

磁场定向控制（FOC）有两种方法：

  q8 d" @. I# Q4 G直接 FOC：转子磁场的方向（Rotor flux angle）是通过磁通观测器直接计算得到的。

间接 FOC：转子磁场的方向（Rotor flux angle）是通过对转子速度和滑差（slip）的估算或测量而间接获得的。

矢量控制要求了解转子磁通的位置，并可以运用终端电流和电压（采用 AC 感应电机的动态模型）的知识，通过高级算法来计算。然而从实现的角度看，对于计算资源的需求是至关重要的。
% c, Q+ f! X& x  M

可以采用不同的方式来实现矢量控制算法。前馈技术、模型估算和自适应控制技术都可用于增强响应和稳定性。

8 k# e7 p2 S% H" J

03

AC电机的矢量控制：深入了解

矢量控制算法的核心是两个重要的转换：Clark变换，Park变换和它们的逆运算。采用 Clark 和 Park 变换，带来可以控制到转子区域的转子电流。这样做充许一个转子控制系统决定应供应到转子的电压，以使动态变化负载下的转矩最大化。

& d. j3 `) R7 a6 P* k3 hClark 变换：Clark数学转换将一个三相系统修改成两个坐标系统：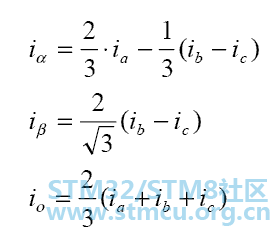

其中 Ia 和 Ib 是正交基准面的组成部分，Io 是不重要的 homoplanar 部分。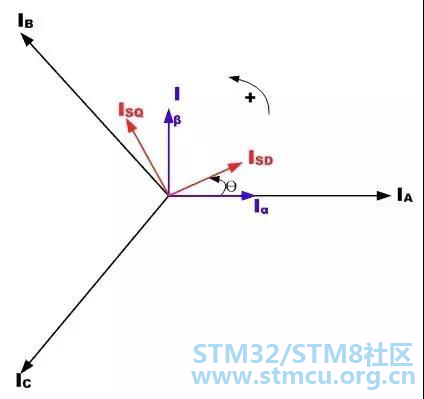
3 M/ }7 J, x9 s- h

图5：三相转子电流与转动参考系的关系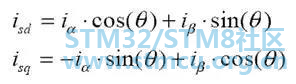
, n, z; Q) w  g+ d) M. Q- L( [

04

Park转换：Park 数学转换将双向静态系统

转换成转动系统矢量

; U" x& h' y* Y5 @' K

两相α，β帧表示通过 Clarke 转换进行计算，然后输入到矢量转动模块，它在这里转动角θ，以符合附着于转子能量的 d，q 帧。根据上述公式，实现了角度θ的转换。

AC电机的磁场定向矢量控制的基本结构Clarke 变换采用三相电流 IA，IB 以及 IC，其中 IA 和 IB 在固定座标定子相中的电流被变换成 Isd 和 Isq，成为 Park 变换 d，q 中的元素。其通过电机通量模型来计算的电流 Isd，Isq 以及瞬时流量角θ被用来计算交流感应电机的电动扭矩。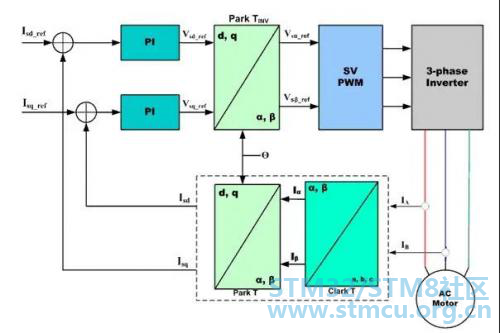

图6：矢量控制交流电机的基本原理

- w; A; ~$ E  B# O- @% I8 U: r

这些导出值与参考值相互比较，并由PI控制器更新。

/ n8 r+ H. y% K- P

表1：电动机标量控制和矢量控制的比较

& ?, `$ `& _6 P

BLDC矢量控制

$ q0 f, Q) u. f# y4 u5 m基于矢量的电机控制的一个固有优势是，可以采用同一原理，选择适合的数学模型去分别控制各种类型的 AC、PM-AC 或者 BLDC 电机。
; e8 H# C: u& K! k6 P& f
" K% U: x5 D5 z, E" s7 @BLDC电机的矢量控制BLDC电机是磁场定向矢量控制的主要选择。采用了FOC的无刷电机可以获得更高的效率，最高效率可以达到95%，并且对电机在高速时也十分有效率。
- w0 q- M) Q% Q# ^: O$ b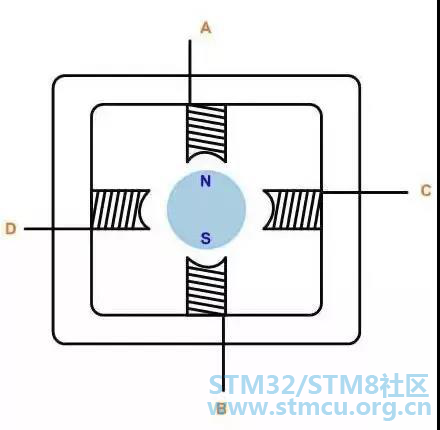
( B* l* T" M; r: L2 L7 l( b

01

步进电机控制

, j( z1 c. l2 z, ?* b- t

图7

; F0 {' X& s6 o. Y+ s; [* i' Y步进电机控制通常采用双向驱动电流，其电机步进由按顺序切换绕组来实现。通常这种步进电机有 3 个驱动顺序：
; t; n: l" N1 _
①单相全步进驱动：

; S9 y6 E* T) k  v+ U6 L5 H

在这种模式中，其绕组按如下顺序加电，AB/CD/BA/DC（BA 表示绕组 AB 的加电是反方向进行的）。这一顺序被称为单相全步进模式，或者波驱动模式。在任何一个时间，只有一相加电。
$ O# G9 u- J$ o- b( E3 \/ j
+ _- p0 h% m8 ^1 X' ?②双相全步进驱动：
7 i. o9 E- E" g- X

+ Z- M9 z3 `* J6 A7 g

在这种模式中，双相一起加电，因此，转子总是在两个极之间。此模式被称为双相全步进，这一模式是两极电机的常态驱动顺序，可输出的扭矩最大。
$ B& t2 q- ?- K8 s) A' a( u8 U$ d5 f
- P  r2 L- c9 @% l: v/ U③半步进模式：

这种模式将单相步进和双相步进结合在一起加电：单相加电，然后双相加电，然后单相加电…，因此，电机以半步进增量运转。这一模式被称为半步进模式，其电机每个励磁的有效步距角减少了一半，其输出的扭矩也较低。

以上3种模式均可用于反方向转动（逆时针方向），如果顺序相反则不行。
# M" L8 ^# \. q
4 |" Y1 X% y9 D/ A1 b% i通常，步进电机具有多极，以便减小步距角，但是，绕组的数量和驱动顺序是不变的。
5 ~# C: z) _  ]" I
1 U+ Q7 O% r% }7 t# ^

02

通用 DC 电机控制算法

通用电机的速度控制，特别是采用 2 种电路的电机：
0 o5 f/ p) _! d. h/ Z9 g
▪ 相角控制
▪ PWM 斩波控制

" |: m- r" X, b9 S" w& D①相角控制

5 r2 ^8 L$ h( e3 L% w

相角控制是通用电机速度控制的最简单的方法。通过 TRIAC 的点弧角的变动来控制速度。相角控制是非常经济的解决方案，但是，效率不太高，易于电磁干扰（EMI）。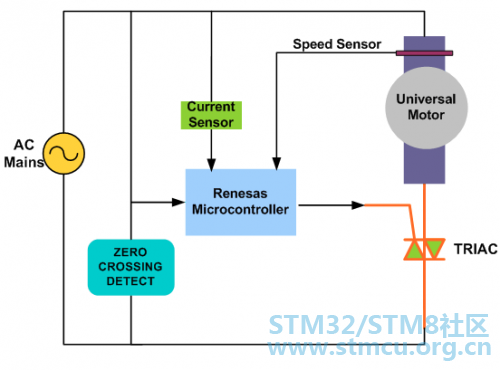

图8：通用电机的相角控制
5 f$ w- X; \+ w( N" r0 U

1 q8 p0 f8 [# G0 f图8表明了相角控制的机理，是TRIAC速度控制的典型应用。TRIAC门脉冲的周相移动产生了有效率的电压，从而产生了不同的电机速度，并且采用了过零交叉检测电路，建立了时序参考，以延迟门脉冲。

②PWM 斩波控制
! y5 S- Q0 e' `4 H5 D

2 ~2 u' x% _6 a8 f

PWM 控制是通用电机速度控制的，更先进的解决方案。在这一解决方案中，功率 MOSFET，或者 IGBT 接通高频整流 AC 线电压，进而为电机产生随时间变化的电压。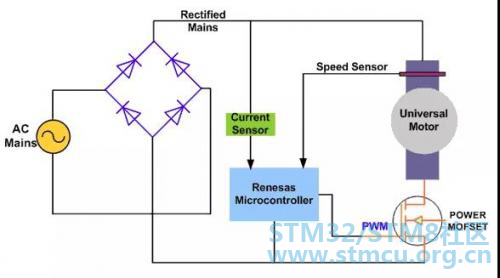
- U; K% D: v$ H7 e4 w

3 ~$ E8 ^% X1 D( Z- m

图9：通用电机的 PWM 斩波控制

2 I6 r9 C5 {" \) w其开关频率范围一般为10-20KHz，以消除噪声。这一通用电机的控制方法可以获得更佳的电流控制和更佳的EMI性能，因此效率更高。