X-Cube-Cryptolib V4

加解密算法是实现信息安全设计的重要工具，在安全启动，安全通信等多个场景都会用到，STM32一直以来都提供支持全系列的算法库软件包X-CUBE-CRYPTOLIB，今年STM32对其加解密算法库又做了进一步的改进升级，发布了V4版本，这个版本的主要亮点有哪些？

接下来我们具体看一下V4版本的加解密库有哪些新变化。

/ e, Z7 `2 s( m1 ?/ R

Cryptolib V4支持的算法

新增加的算法
0 y) J4 B# O" y; E7 a4 }5 {5 Z; ]

·支持国密SM算法
-SM4 (CBC, CFB, CTR, ECB, OFB)
4 Z, r9 x8 k- w6 v+ F-SM3
-SM2 (密钥对生成，计算ZA，签名，验签）
* Z& W. f# ]2 G1 J: [# O

$ f" ~4 v% y  t) U0 k·散列算法
1 Y& _: z# Y2 ?5 p! H) t除了SM3，还增加了SHA3 (SHA3-224, SHA3-256, SHA3-384, SHA3-512) 和SHAKE


# ^" M5 H  x" s8 E' N& N·MAC算法
HMAC (SM3), KMAC (SHAKE)
1 G  Q/ g, t/ C' O

·ECC椭圆曲线算法
除了SM2，还增加了ECDSA的Ed448


# T! h) |/ u0 U4 z$ t" X: R·ECDH算法
增加Curve448


6 D9 w$ Z$ k  }  A+ ^·RSA算法
新增加PKCS#1 V2.2 以及 RSA CRT模式（包含抵御Bellcore攻击的防护）
# s& D' ~3 f; [# j2 T5 G
; s3 h: W; }% [7 A: S2 m5 Q: C
·随机数生成
! Z8 K  K. o  x4 `增加CTR_DRBG_AES256

不再包含的算法
/ k( y' M# x3 I4 M; J
! B3 k3 b% X# O2 e·部分旧的算法，处于安全性考虑不推荐使用，因此在V4中不再包含，例如
4 ]5 l! D  I5 h  k4 @块加密算法中的ARC4, DES, TDES
" K" G" Q$ k( c' V# J4 k$ ~散列算法中的MD5

6 u& _) g7 p) ]& h
·密钥派生算法HKDF
! W+ g! M) ?% j; ~. ]4 n% r. IV3中包含的HKDF-512算法在V4中不直接以库的形式提供
: P  x2 N& h# N# y在ST wiki页面中会说明如何在HMAC基础上实现HKDF

软件包内容

新的软件包架构

新版本采用了新的软件包架构


加解密库仅按照内核提供（每个内核对应一个加解密库）
加解密库不再按照STM32系列分别提供
加解密库不再区分编译器和优化方式（Speed、Size、FPU）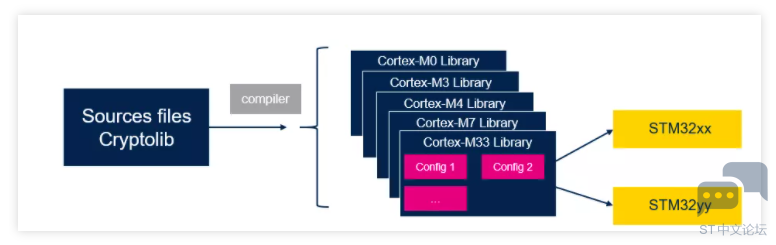
4 [8 v5 J  Z6 v9 u

V4的目录结构 vs. V3的目录结构

- [* n) L3 [7 p& Q* d: O# lV3软件包的目录结构是每一个STM32系列对应一个单独的目录
* W2 S3 R) X+ d: ^5 q- }0 Z6 y

7 k, \' V! D, }% X" u) _% o每个芯片系列都有对应的Middleware目录, 里面包含加解密库
加解密库有多个库文件，分别针对不同编译器以及不同的优化选项
! k4 q- ^% U* `参考例程工程同样也在每个STM32系列子目录的Projects目录中。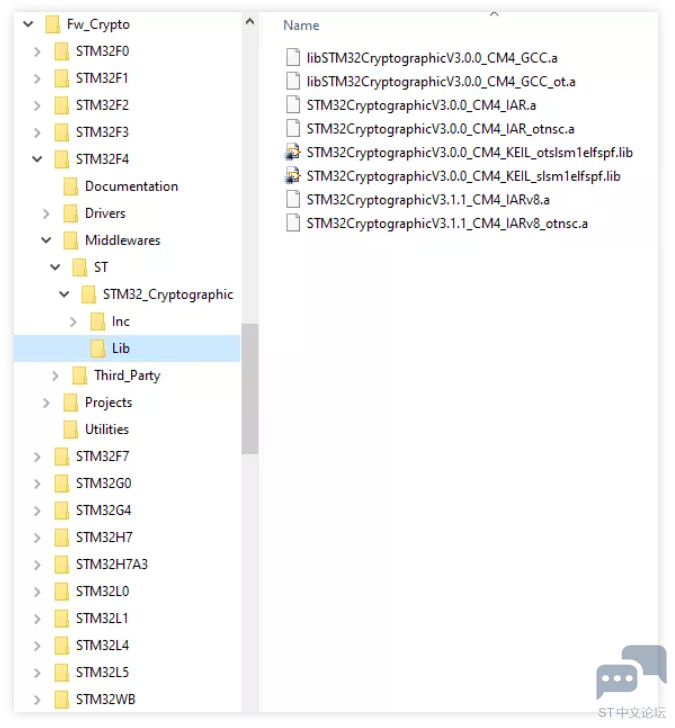
) y5 @1 Y$ v9 F  K0 Z7 l: v

V4的目录结构则完全兼容Cube/X-Cube软件包（STM32Cubexx / X-Cube-xxx）架构，方便与Cube/X-Cube包进行集成。
% B/ {( o, B. x% h+ g

  d4 q1 ^) T7 p* `1 ~' W6 WV4中包含加解密库的Middleware文件夹直接在顶层目录
/ |5 x4 Q2 r1 U2 ?& `3 r' \8 `lib目录下的库文件不针对每个STM32系列，也不再区分不同的编译器和优化方式
' a2 X5 ^) w" G- Z加解密库文件按照Cortex内核版本，每个内核提供一个统一的库文件
同一个库文件可以适用于各种编译器（AEABI兼容）
对于不同优化选项的选择可以在链接阶段进行配置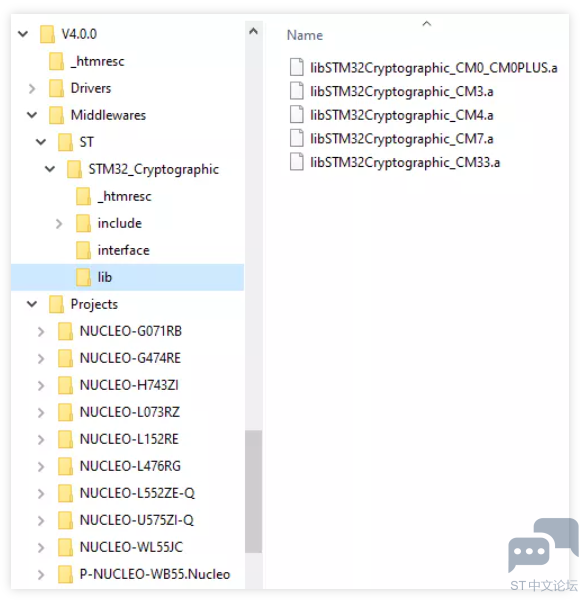

V4的参考例程则类似Cube/X-Cube包的结构，在Projects目录下的各个系列的子目录中提供。

新版本示例工程支持的系列包括
, h1 j, m7 }+ O0 ]

- v- m2 F4 G+ N4 aSTM32G0，STM32G4
2 H/ }0 g1 R/ b& {3 vSTM32H7
STM32L0，STM32L1，STM32L4，STM32L5，STM32U5 (V4.0.1中包含)
6 D7 h/ F" Z/ {$ b8 pSTM32WB，STM32WL

# S" q, d8 W$ s; f
3 y* X7 h* z5 ?. f/ K. d8 N其他STM32系列虽然没有提供直接的参考例程，但也可以参考示例代码的方式使用库文件，因为库是针对不同Cortex®-M内核提供的，并不区分产品系列。

  d  n8 {  }8 j" n) T! p代码质量进一步提升
( K% x. Q* d6 |4 L$ d& c# l
V4版本加解密库的源码经过MISRAC:2012检查，加解密库的头文件也同样符合MISRAC:2012标准，对于有MISRAC合规需求的场景，V4将提供很好的支持。
7 G$ Q& I2 V  c+ Q0 P2 E
' x8 H. H, r, b# h$ `/ g更小代码+更高性能

V4的加解密库在优化方面做了很多提升。以STM32G4为例，我们可以用下表对比一下使用CryptoLib V3.1.3和V4.0.0版本，选择最高性能配置时的运算速度比较。可以看到，无论是对称算法，散列算法还是非对称算法，V4在性能上都有了很大提升，同时加解密库的代码量比V3还要更小。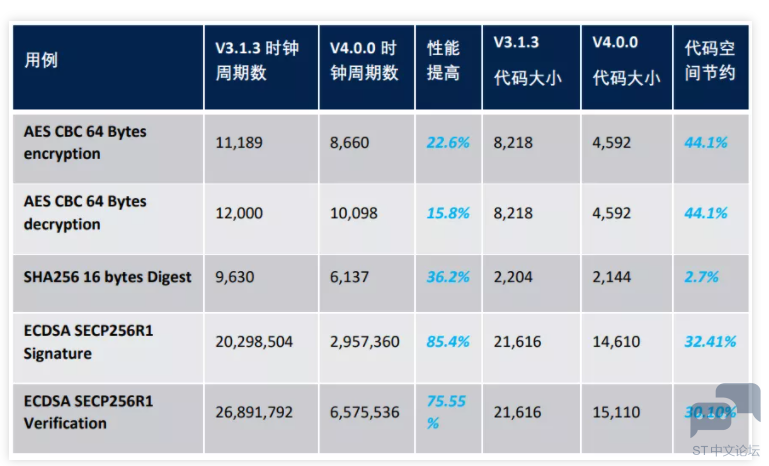

更加灵活易用

3 F& M4 g) D& i; N* e* p( B5 Y- L6 D方便灵活的方式选择加解密库的实现配置

' [5 I. H* B0 r! S+ L" r  r* TV4的加解密库为每个内核提供一个单一的库文件，但是允许客户在其应用工程中可以根据速度和代码大小的需要选择不同的配置。这个配置在链接和使用过程中完成。
9 E, u+ _; Z8 h5 a) \1 @! b' M

4 f1 N- u$ r5 u* H: nV3的加解密库在编译阶段使用不同配置，编译出不同的库文件
而V4在相同的算法服务中实现了对不同配置（性能高低和代码量大小）的支持
用户通过Construct API或者每个服务的Processing API来进行选择采用哪个实现
) n8 x: l' u. B: A$ E9 Z( Z缺省的配置以头文件形式提供

( g& m  j& E' x5 o% T. c4 ^" l- n以ECDSA签名算法为例，使用签名函数之前，首先需要调用cmox_ecc_construct（）函数，这个函数的第二个输入参数CMOX_ECC256_MATH_FUNCS就用来选择下层的具体实现使用哪一个。
" e% O! S1 [9 `# |( Z

CMOX_ECC256_MATH_FUNCS的定义决定了ECDSA的处理函数将会选择哪个实现，缺省配置为CMOX_MATH_FUNCS_SUPERFAST256，可选配置包括
6 c1 j! s0 W  T

CMOX_MATH_FUNCS_SMALL ：代码量小，性能相对低
CMOX_MATH_FUNCS_FAST ：性能高，代码量相对大
# F' t/ ]& }' t0 Z+ e( L9 V* c9 S! M4 |CMOX_MATH_FUNCS_SUPERFAST256：性能更高（针对长度为225到256的ECC曲线）
1 s/ i4 N, B: C7 e: C4 t
" K) Z2 Y* m& A( |( w* A其他算法的配置也可以使用类似的方法进行性能和代码量大小的选择，具体请参考Middlewares\ST\STM32_Cryptographic\include\cmox_default_config.h
8 S# w0 |( E: e% P

/ b9 h3 D7 |; }如果希望所有的配置都按照最小代码量来选择，则可以直接使用相同目录下的cmox_small_config.h头文件的定义，如果希望所有配置都按照最高性能来选择，则可以直接使用相同目录下的cmox_fast_config.h头文件的配置。
8 z& E  a1 C( ^8 v2 @! b

应用代码调用更加简洁
同样以ECDSA为例，使用V3版本加解密库，应用程序需要调用多个API才能完成 一个ECDSA Verification，而使用V4的加解密库只需要两个API即可完成。
# d- [- T# R6 q( k$ i2 Q% \

V3

1. int32_t rv;
   
2. EC_stt EC_st;
   
3. membuf_stt Crypto_Buffer;
   : ?& q& T- i' T" p5 J! Y
4. ECpoint_stt *PubKey = NULL;
   " p* p- o+ q" I. i0 `9 _; U! ]
5. ECDSAsignature_stt *sign = NULL;
   
6. uint8_t membuf[MAX_MEMBUF_SIZE];
   
7. ECDSAverifyCtx_stt verctx;
   
8. 
   % n  u+ M* p5 K, O) m' ]" F# S
9. uint8_t pub_x[] = {…}, pub_y[] = {…};
   
10. uint8_t sign_r[] = {…}, sign_s[] = {…};
    6 Z3 S; h# d( M: f1 I2 k
11. uint8_t digest[] = {…};
    
12. 
    
13. Crypto_Buf.pmBuf = membuf;
      P8 q5 W: Y+ n( R9 A
14. Crypto_Buf.mUsed = 0;
    % k7 R& B3 z) A
15. Crypto_Buf.mSize = sizeof(membuf);
    2 P9 o2 {- M8 R& n
16. 
    
17. /* Init the EC main struct */
    8 V# r, b8 `/ ^( m' q
18. rv = ECCinitEC(&EC_st, &Crypto_Buf);
    4 D4 d; V2 U" Q3 P
19. 
    
20. /* Init the public key */
    ! R# W" F& n5 n, m3 ~: o
21. ECCinitPoint(&PubKey,
    9 t1 G, y4 ?. S/ g
22.              &EC_st,
    
23.              &Crypto_Buf);
    5 [1 Y& g7 b( G& Z/ L1 ^
24. ECCsetPointCoordinate(PubKey,
    + W& `% Q0 u* c* m7 _4 U  Q
25.                E_ECC_POINT_COORDINATE_X,
    
26.                pub_x,
    / h7 f1 b. |2 x) Q
27.                sizeof(pub_x));
    
28. ECCsetPointCoordinate(PubKey,
    . {3 M* a* h$ D. M- c' e
29.                E_ECC_POINT_COORDINATE_Y,
    
30.                pub_y,
    - u3 ?# t8 O1 K: r
31.                sizeof(pub_y));
    
32. 
    
33. /* Init the signature */
    * S! [/ o+ T" }+ l+ C) ]& d
34. ECDSAinitSign(&sign,
    
35.               &EC_st,
    ' i% h9 ~: ]7 L, L' }4 ^
36.               &Crypto_Buf);
    
37. ECDSAsetSignature(sign,
    : q5 n* u8 K6 |. L) J
38.               E_ECDSA_SIGNATURE_R_VALUE,
    & f& }* @7 R! u+ O1 b/ G  D# `& \3 e
39.               sign_r, sizeof(sign_r));
    
40. ECDSAsetSignature(sign,
    / K# A& l7 w3 M
41.               E_ECDSA_SIGNATURE_S_VALUE,
    2 W6 ]2 `2 N. y2 I2 ?) K
42.               sign_s, sizeof(sign_s));
    
43. 
    8 b3 ]* Q8 b% `3 m/ G/ F
44. /* Verification */
    1 h/ i& Q, [' d! t
45. verif_ctx.pmEC = &EC_st;
    
46. verif_ctx.pmPubKey = PubKey;
    : g3 \  @' f2 d8 l
47. rv = ECDSAverify(digest,
    0 X9 q1 W/ Q/ ^* ~1 B& c! E
48.                  sizeof(digest),
    
49.                  sign,
    
50.                  &verif_ctx,
    7 k0 _4 t  ^+ G6 ^* h: X
51.                  &Crypto_Buf);

复制代码

V4

1. 
   3 h: [' {  Q# D* Z' N
2. cmox_ecc_retval_t rv;
   
3. cmox_ecc_handle_t Ecc_Ctx;
   
4. uint8_t membuf[MAX_MEMBUF_SIZE];
   
5. uint32_t fault_check = CMOX_ECC_AUTH_FAIL;
   , H. y' H: [/ g4 o8 N$ j
6. 
   
7. uint8_t pubkey[] = {…}, digest[] = {…};
   
8. uint8_t signature[] = {…};
   & A& w' Q( e& [+ [- d
9. 
   " v) l4 d* L! T' i7 w8 a
10. /* Construct a ECC context */
    6 K5 a, P, e  Z5 |. z
11. cmox_ecc_construct(&Ecc_Ctx,
    ) `. n% q, E+ M, |& m( R! f. ~
12.         CMOX_ECC256_MATH_FUNCS,
    ) L. m. b, N4 W
13.         membuf, sizeof(membuf));
    , h3 L# V3 s# I2 Q2 v
14. 
    
15. /* Verify directly the signature passing
    
16.    all the needed parameters */
    ' Z& P5 G% D3 s# q: I; x
17. rv = cmox_ecdsa_verify(&Ecc_Ctx,
    3 l/ }9 H" Q+ `9 F# J
18.         CMOX_ECC_CURVE_SECP256R1,
    
19.         pubkey, pubkey(Public_Key),
    
20.         digest, sizeof(digest),
    
21.         signature, sizeof(signature),
    
22.         &fault_check);

复制代码

从V3到V4的快速切换



$ z/ D8 x  i8 E1 f2 J7 j0 a
在V4的软件包中，还提供了一个wrapper实现，帮助以前V3的使用者快速切换到V4的，这个wrapper允许应用继续沿用V3 API但使用V4的库。当然，这种用法虽然快速切换到V4，但却不能最大化地利用V4的新优点，不是推荐用法，仅仅作为快速切换的目的使用。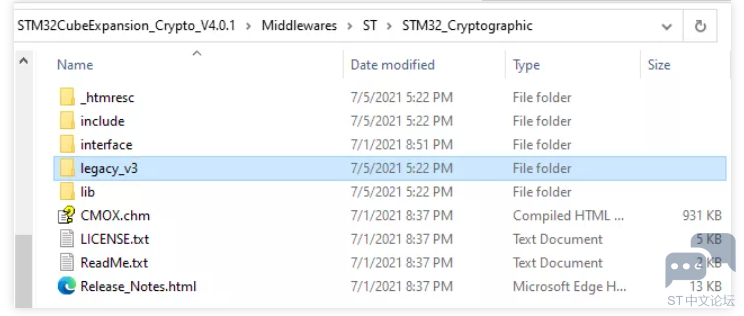

算法认证

V4提供的加解密库经过了NIST CAVP（Cryptographic Algorithm Validation Program）的认证。
0 Q+ D6 K/ B- t- z- _
# @! d( i+ \# B7 f/ d
( C' M) r6 j3 g认证测试覆盖了不同的性能和代码大小的配置方式（前面提到的可以通过头文件的宏定义进行的配置选择）
1 ~: c: y; o4 @0 ?; |认证基于Cortex®-M内核，而不是和某个特定的STM32系列绑定，所以可以适用于所有STM32系列
# S! v* P! X! g
有关加解密库认证的详细信息可以参考此链接：https://wiki.stmicroelectronics. ... rary_Certifications

7 p& _. f0 i5 m, M
% d; Q6 W6 V& f/ q( s

资源链接

文档
9 o2 u2 p" M' T# ?/ w所有Cryptolib V4相关的文档都通过STM32 MCU Wiki以网页形式提供，不再提供单独的UM和其他文档：https://wiki.st.com/stm32mcu/wiki/Category:Cryptographic_library

" ~, ]3 s5 Y3 ?. g4 L5 d
/ E0 Q0 v5 |8 ~* g- R内容包括


加解密库简介、使用指南、密码学算法的基础知识
( A8 P2 V/ M+ W1 e  O0 u9 V4 h

如何安全地使用加解密库、如何实现HKDF、加解密库认证信息、如何迁移到新版加解密库

加解密库的性能及资源占用信息

下载页面
$ |0 l- Q. \' a7 }; L" w9 ^: U) vV4版本加解密库可以从XCUBE-CRYPTOLIB常规的网址下载：
1 A( {6 m" `7 `) n8 u+ `  ]https://www.st.com/en/embedded-software/x-cube-cryptolib.html
( s6 M3 V$ C4 n# q

V3版本加解密库可以通过以下链接下载：
https://www.st.com/en/embedded-software/x-cube-crypto-v3.html

1 y! S6 ?. }( j4 A
# G+ z% Y: t8 p

/ K  t' |/ i+ M6 E6 I