【经验分享】如何使用STM32提供的DSP库进行FFT

[复制链接]

STMCU小助手发布时间：2022-1-15 23:08

文章
文章封面:
文章简介:	前些日子，因为需要在STM32F103系列处理器上，对采集的音频信号进行FFT，所以花了一些时间来研究如何高效并精确的在STM32F103系列处理器上实现FFT。在网上找了很多这方面的资料做实验并进行比较，最终选择了使用STM32提供的DSP库这种方法。

前些日子，因为需要在STM32F103系列处理器上，对采集的音频信号进行FFT，所以花了一些时间来研究如何高效并精确的在STM32F103系列处理器上实现FFT。在网上找了很多这方面的资料做实验并进行比较，最终选择了使用STM32提供的DSP库这种方法。

　　本文将以一个实例来介绍如何使用STM32提供的DSP库函数进行FFT。

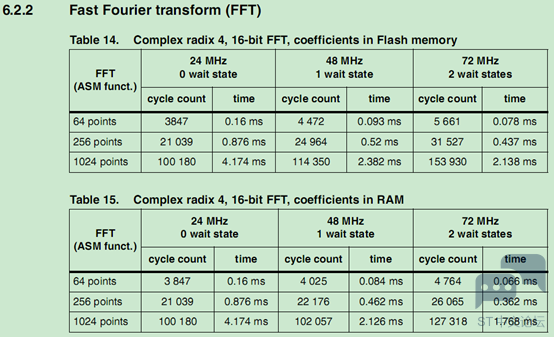
1.FFT运算效率

　　使用STM32官方提供的DSP库进行FFT，虽然在使用上有些不灵活（因为它是基4的FFT，所以FFT的点数必须是4^n），但其执行效率确实非常高效，看图1所示的FFT运算效率测试数据便可见一斑。该数据来自STM32 DSP库使用文档。

图1 FFT运算效率测试数据

　　由图1可见，在STM32F10x系列处理器上，如果使用72M的系统主频，进行64点的FFT运算，仅仅需要0.078ms而已。如果是进行1024点的FFT运算，也才需要2.138ms。

2.如何使用STM32提供的DSP库函数

2.1下载STM32的DSP库

2.2添加DSP库到自己的工程项目中

　　下载得到STM32的DSP库之后，就可以将其添加到自己的工程项目中了。

　　其中，inc文件夹下的stm32_dsp.h和table_fft.h两个文件是必须添加的。stm32_dsp.h是STM32的DSP库的头文件。

　　src文件夹下的文件可以有选择的添加（用到那个添加那个即可）。因为我只用到了256点的FFT，所以这里我只添加了cr4_fft_256_stm32.s文件。添加完成后的项目框架如图2所示。

图2 项目框架

2.3模拟采样数据

　　根据采样定理，采样频率必须是被采样信号最高频率的2倍。这里，我要采集的是音频信号，音频信号的频率范围是20Hz到20KHz，所以我使用的采用频率是44800Hz。那么在进行256点FFT时，将得到44800Hz / 256 = 175Hz的频率分辨率。

　　为了验证FFT运算结果的正确性，这里我模拟了一组采样数据，并将该采样数据存放到了long类型的lBufInArray数组中，且该数组中每个元素的高16位存储采样数据的实部，低16位存储采样数据的虚部(总是为0)。

　　为什么要这样做呢？是因为后面要调用STM32的DSP库函数，需要传入的参数规定了必须是这样的数据格式。

　　下面是具体的实现代码：

/******************************************************************. v1 V+ N" h( D3 V
函数名称:InitBufInArray()
1 v- J2 ] M. F) Y' D8 D4 h0 j
函数功能:模拟采样数据，采样数据中包含3种频率正弦波(350Hz，8400Hz，18725Hz)2 K1 n" U+ F: V' J* l/ F7 m
参数说明:
m+ A! S* m: y& i! v
备注:在lBufInArray数组中，每个数据的高16位存储采样数据的实部，
" r/ H/ }; ` s' D" r5 ~3 o
低16位存储采样数据的虚部(总是为0)8 T4 [& |: e. h
作　　者:博客园依旧淡然（http://www.cnblogs.com/menlsh/）
( c' A# i: w1 J2 b
*******************************************************************// M) d" {' ?2 h; d
void InitBufInArray()
- Y# E3 C# o/ {9 l/ @% Z
{
; i) n9 M9 u H0 }$ T$ i# Y
unsigned short i;
& D. j. U2 y7 @2 l2 M1 S
float fx;1 T2 }; `$ f& N- n7 i
for(i=0; i<NPT; i++)
! v: H0 m! {7 u7 U. q5 P: q
{1 q: }) r- D0 L
fx = 1500 * sin(PI2 * i * 350.0 / Fs) +
9 P; i9 o7 E; Q3 y0 f% r0 I
2700 * sin(PI2 * i * 8400.0 / Fs) + B% J+ f4 l) y' ?: V* H" V# F
4000 * sin(PI2 * i * 18725.0 / Fs);5 b% m3 V2 j7 O' d
lBufInArray[i] = ((signed short)fx) << 16;- U% ]5 n B/ P% s$ x
}
' k* X$ K! q, V D( M
}

复制代码

　　其中，NPT是采样点数256，PI2是2π（即6.28318530717959），Fs是采样频率44800。可以看到采样数据中包含了3种频率的正弦波，分别为350Hz，8400Hz和18725Hz。

2.4调用DSP库函数进行FFT

　　进行256点的FFT，只需要调用STM32 DSP库函数中的cr4_fft_256_stm32()函数即可。该函数的原型为：

　　void cr4_fft_256_stm32(void *pssOUT, void *pssIN, uint16_t Nbin);

　　其中，参数pssOUT表示FFT输出数组指针，参数pssIN表示要进行FFT运算的输入数组指针，参数Nbin表示了点数。至于该函数的具体实现，因为是用汇编语言编写的，我也不懂，这里就不妄谈了。

　　下面是具体的调用实例：

　　cr4_fft_256_stm32(lBufOutArray, lBufInArray, NPT);

　　其中，参数lBufOutArray同样是一个long类型的数组，参数lBufInArray就是存放模拟采样数据的采样数组，NPT为采样点数256。

　　调用该函数之后，在lBufOutArray数组中就存放了进行FFT运算之后的结果数据。该数组中每个元素的数据格式为；高16位存储虚部，低16位存储实部。

2.5计算各次谐波幅值

　　得到FFT运算之后的结果数据之后，就可以计算各次谐波的幅值了。

　　下面是具体的实现代码：

/******************************************************************# X$ m3 c4 B9 ~ ]8 G7 S9 B
函数名称:GetPowerMag()
5 S _8 l4 X6 s
函数功能:计算各次谐波幅值
& e7 c) \7 x& M" I0 R! _- G* b
参数说明:
+ e9 J4 k7 L- d. t' z( ]$ l
备　　注:先将lBufOutArray分解成实部(X)和虚部(Y)，然后计算幅值(sqrt(X*X+Y*Y)) G4 N0 m E" e# h6 o `9 H
作　　者:博客园依旧淡然（http://www.cnblogs.com/menlsh/）. Z! T! Y( B/ F; |$ D% P) F' t
*******************************************************************/
' D. n: |0 l# H6 @! l
void GetPowerMag()
' O! \5 H+ x8 u& g$ N& t
{# W; d$ {/ K' C
signed short lX,lY;" k5 _5 {/ v9 M1 m8 n
float X,Y,Mag;, Y% X( U: |, }9 R- p
unsigned short i;6 v0 R' L$ b1 ^4 G. M
for(i=0; i<NPT/2; i++)% |5 L. C" G( ?; r3 \4 M
{& G; [. t4 K. B+ D G/ ^: K& @- P
lX = (lBufOutArray[i] << 16) >> 16;
# I, x9 [) K: _6 }+ n. B' l7 g
lY = (lBufOutArray[i] >> 16);; q |+ S" S4 I; Z! `" X* H
X = NPT * ((float)lX) / 32768;7 ]1 ?8 f% m2 n0 Z% N$ B
Y = NPT * ((float)lY) / 32768;. C1 S: G" E5 W# b7 w; m0 z- q/ t
Mag = sqrt(X * X + Y * Y) / NPT;
: H# j$ C( x d) u
if(i == 0)6 c$ i9 y! ]. \
lBufMagArray[i] = (unsigned long)(Mag * 32768);3 @/ z7 M! w: [+ b" F3 d6 k
else2 o+ N9 v) a# W- a2 ?. e
lBufMagArray[i] = (unsigned long)(Mag * 65536);% ^# l1 t" C; {- |6 s
}: ]( ]8 X5 B" x7 ?) M5 B
}