对于STM32内部ADC采集时候，难免会受到外部干扰的，导致数据不稳定情况。一般在实际使用过程中，我们就需要对增加采样次数来提高分辨率的技术。而STM32cube MX 软件自带过采样的功能。下面就和大家介绍一下STM32如何使用软件配置过采样的功能，从而实现数据的稳定性。

3 P' _! Z5 H* a- v0 n下面和大家具体分享一下软件配置步骤和注意事项：
一：过采样的基本知识分享：
0 _6 E2 y% \7 Q3 H8 B, N' I; Q
1.1 基本的原理：使用STM32通过多次采取ADC的数据，并对结果进行取平均值处理，提高有效分辨率。每增加４倍的采样次数，分辨率可提高１位；我们在实际的使用过程中，可以根据自己的需求进行设置和更改。

二：软件配置步骤

+ N/ }6 Z5 C8 {2.1 配置ADC

: W' j3 w: E' o/ o1 W/ Z选择ADC通道：确定要采样的模拟输入通道。

设置采样时间：根据信号特性调整采样时间。
- X9 S) t& g! I- K8 p: O, p
配置ADC分辨率：通常设置为12位。
" F; ^5 |8 y) Q+ S7 O
2.2 配置过采样

设置过采样比率：例如16倍过采样。

设置右移位数：根据过采样比率调整，如16倍过采样需右移2位。

2.3 启动ADC
" V# h7 g$ t& q+ ~7 M/ a1 S3 |' v1 t
启动转换：ADC开始采样并存储结果。
' E5 u& D7 c0 C1 e; K% c
等待转换完成：通过轮询或中断方式检查转换状态。
$ D" \2 d9 k" w
7 M4 p2 ^. U' p# r/ c' \2.4 读取和处理数据
0 [/ ]8 s+ X( M$ ~8 Z
: w# I+ S& q$ M' T/ p. }读取ADC数据：从数据寄存器获取采样值。

计算平均值：对多次采样结果取平均，得到最终值。

: [1 g* d# B6 bSTM32 cube MX 软件配置如下：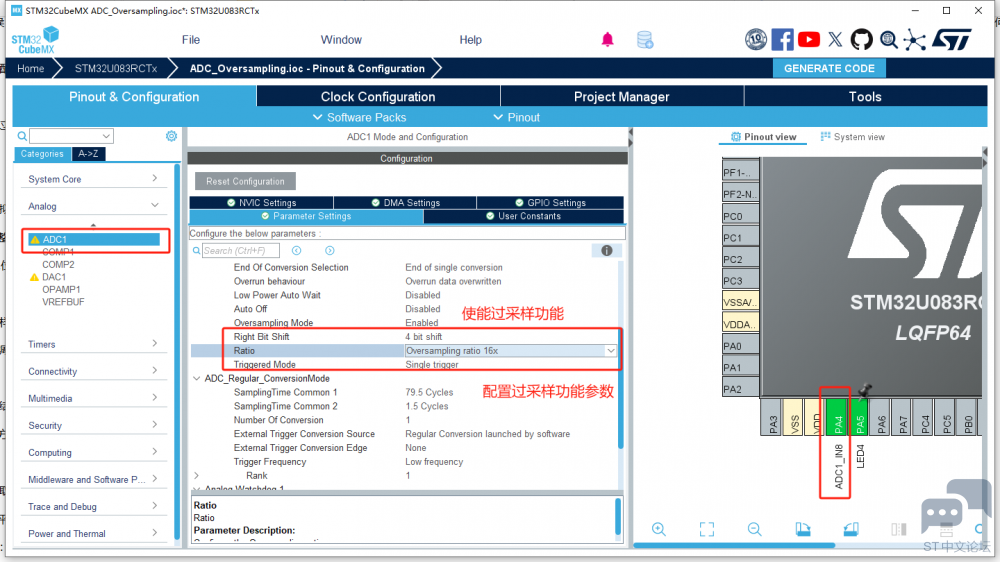
; z( C! ^! s3 O" N" n
2 m. k) i$ l9 M2 U9 |) c2 N
) L) M# Y0 A. o, Q: ?! K
" ?8 H/ s) @# i" Z$ H主要代码如下所示：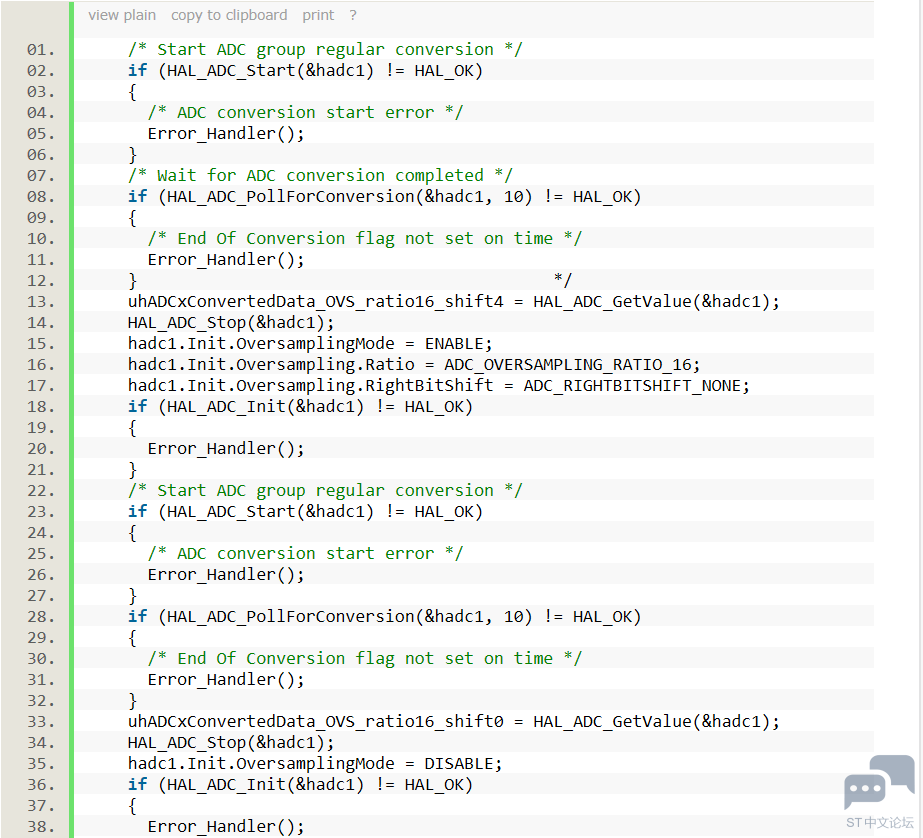
8 R" E2 u& U- j$ b
: ?. z% t3 _* m8 B' L3 Y3 g0 `

$ I$ z" e' z/ S& @5 u. t5 G                                                                                                                                                                                                         ADC 配置为在单转换模式下从 SW 触发器转换单通道。ADC 过采样功能与 3 个设置一起使用：

* l  |9 j! j+ p. T4 @3 n' d       第一步：启用 ADC 过采样：比率 16，位右移 4。
* ~' b" e1 b3 ^- T+ ~# v
       第二步：启用 ADC 过采样：比率 16，无位元右移。

) q3 ]# a& D! O: H- N       第三步：禁用 ADC 过采样。

       程序循环执行，上述步骤代码；
3 A9 L0 n% [& d* M
' \/ D' n/ t2 h! X2 u$ N        示例执行：
% [! h/ y6 r9 w- V
3 q/ Q$ n2 m, j! i9 a' [- f        在主程序执行中，ADC 组使用 3 个过采样设置定期连续转换所选通道。

7 g& z4 F3 G2 r; Q; F, Z        然后，对数据进行评估：

         数据范围有效性检查

/ j) O) o1 s( v/ r, K  ?        用户可以评估过采样的预期结果：启用过采样的 ADC 转换数据比禁用过采样的 ADC 转换数据的变化更小。
0 x3 B# P  C: j' g# R: v
9 ~3 }, O& O+ X" C+ e: `        对 16 位的过采样转换数据进行软件计算，以获得相当于浮点分辨率 12 位的精确数据。
. V" \% Y  T& b
) z/ T* q+ O% t         程序仿真效果如下所示：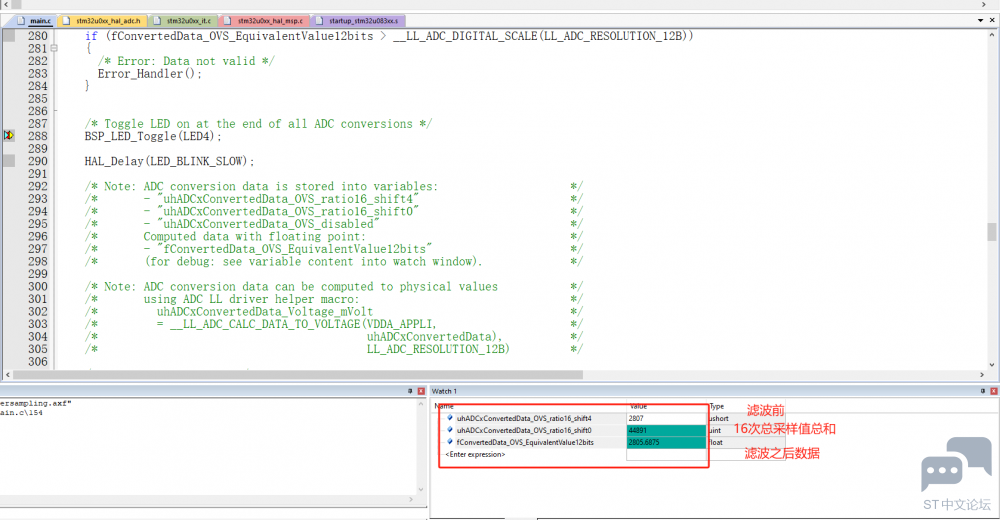

        
2 u: Q2 D: W! Y* B
                                                                                                                                                                                                           注意事项：

         噪声水平：过采样适用于噪声较大的信号。
; w' R' m( b  T% X$ _* I
0 g: o  |3 Q. Z9 Y1 i        采样时间：确保采样时间足够捕获信号。
6 g8 }- P3 y* T0 I6 T/ l" s
         时钟频率：ADC时钟频率需满足过采样要求。
& ]2 A6 l. j# V. D+ _6 [
; p; R0 R6 u+ l# C          项目总结：

          STM32 ADC过采样通过增加采样次数提高分辨率，适用于需要高精度但硬件分辨率不足的场景。合理配置过采样比率和右移位数是关键。
9 |5 K0 e4 o3 z8 Z
. v1 [8 v6 f' q0 o8 Q         几种常用得滤波算法分享：
1 X+ h/ g  c6 p7 c! L8 ]
         1：一阶互补滤波算法：

         取值：k = 0-1，本次取值滤波结果　＝（1-K），本次采样值需要加上上次滤波得结果数据

         代码如下所示：

, I6 @8 g3 A  q- ]/ T         

         从代码中，我们可以看到该种滤波算法还是有很大得弊端的，效果比较一般，对于高精度的场合不建议使用。

          2: 采用中值算法滤波

( v" j. ]" w. X5 }( O7 N! R          主要是程序在执行的时候，连续采集N次（需要注意下这里下，这里的N必须取值奇数），程序需要按大到小或者从小到达的顺序进行排序，然后取中间数值做为有效值。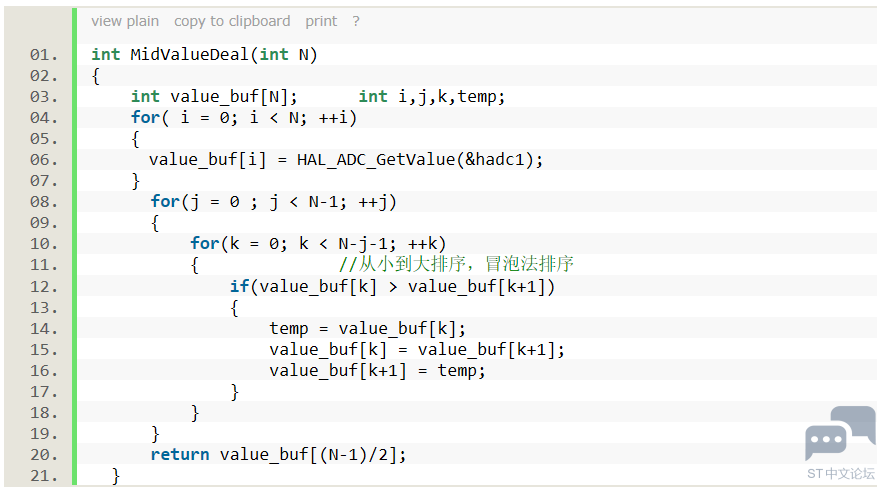

4 X' \) f: C6 K7 t$ K          代码如下：
( [: F6 a, ?: y) y5 q
. Y/ Q& e5 v+ ^" Z3 [8 Y5 x! l  

* a) {. M. `! `* i  t% U
! B! E% f! q% w; v2 t3 T可以有效的去除数据因为外界干扰引起的数据的波动，对一些大滞后系统：比如温度、液位等变化缓慢的有良好的滤波效果，上述代码可以有效消除异常数据和平稳变化的采样值效果比较好；

6 S( ^* G7 W  D        3：算术平均数滤波

        连续取值N个数据，对所有的数据进行取平均值；

         代码如下：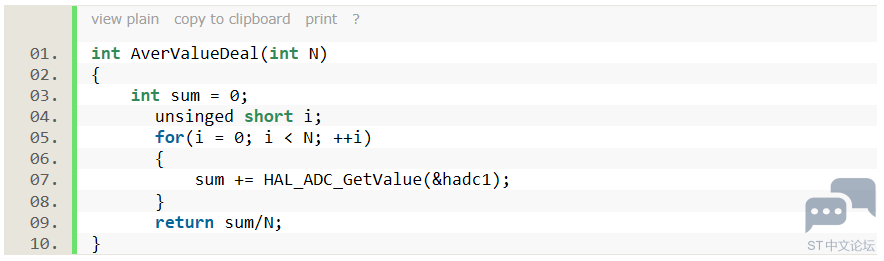
$ s! V# Z- o# N  G' |  ?
        
                                                                                                                                                                                                             这里取值时候，需要根据被控对象进行选择，N值取值过大，会导致响应过慢，数据的灵敏度过低，所以采用算术平均值滤波时候，需要我们格外的注意；

* |5 H6 I! O; A/ y         4:滑动滤波算法

% M7 M# S4 F" T6 d+ o          把连续取N个采样值看成一个队列，队列的长度固定为N。每次采样到一个新数据放入队尾，并扔掉原来队首的一次数据(先进先出原则)。把队列中的N个数据进行算术平均运算,就可获得新的滤波结果；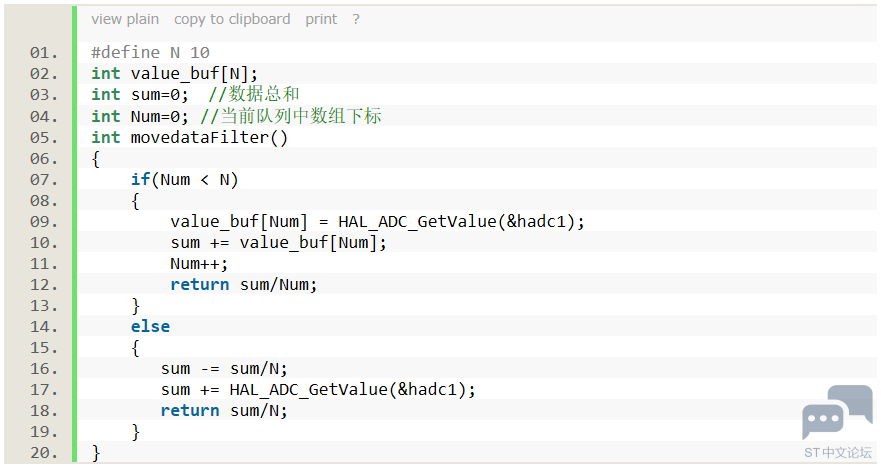
* [- p5 T( h- V
8 [0 i' R( y' @/ a- s5 l! e                                                                                                                                                                                                            好了，几种常用的滤波算法，已经和大家分享完毕，欢迎大家相互讨论。

7 s7 K* \+ O. {3 D