在STM32的应用开发过程中，我们有时可能涉及到DSP应用，需要使用到相关DSP函数。这里基于STM32H743芯片的Nucleo开发板，做个有关矩阵运算应用的演示，简单的演示下两个矩阵相乘的实现过程。

2 K8 w5 B$ a( n8 J) C开发环境选择的是ARM MDK，当然你也可以选其它的，比方IAR, STM32CubeIDE等。
) j: Y; g5 J* c2 m" s- A
  x) ]& T2 v; e
, {7 Z1 _. U: X3 [0 L  e1 j我们要用到ARM提供的DSP函数库，该库在STM32的Cube库或标准库里都可以找到。

9 K3 `; O3 n$ M9 `6 W
以STM32CubeH7的库为例，相应的DSP函数库一般在下面位置：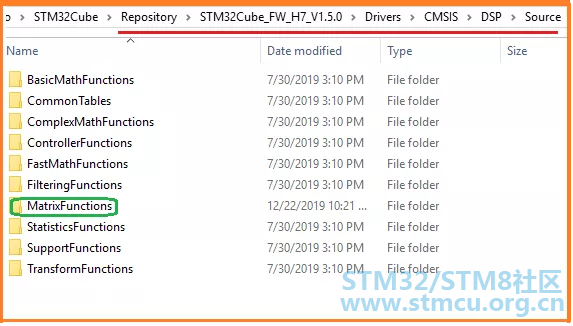
& Y% N. b) p+ h* B" r+ `
, m. H2 d. N1 Y  N' |



4 H0 @3 U# O% F8 r上图中绿色方框内的函数即为跟矩阵相关的函数库文件。

$ s7 x# i4 O1 f6 ]8 T5 e
具体使用时，我们直接添加相应的lib库进来即可，不过，添加该lib库文件时要注意两点：
0 n6 ?% u' Y! W

你选择的库文件要跟你芯片类型一致，内核类型、大小端模式、是否支持浮点运算。


你选择的库文件还要跟你所使用的编译器匹配，即IDE是MDK还是IAR等。

% b2 f( [4 {6 T' P7 M
' l2 s; I8 X( }( m! H6 O基于上面两点我们添加arm_cortexM7lfdp_math.lib文件【corex M7、小端模式、支持硬件浮点单元】。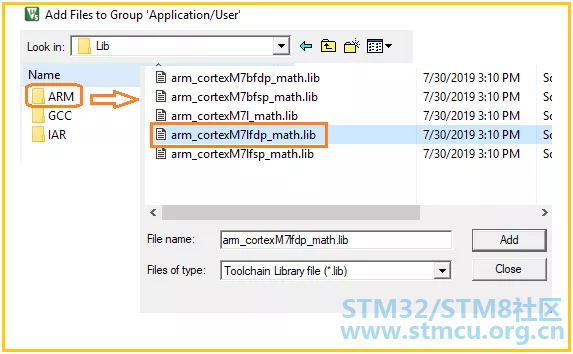


( x$ R/ H1 G- d8 o% S' M1 n; I" z


( Z2 d! q3 F, I8 F8 \) f* a! g6 J在我们的main()文件里添加arm_math.h头文件。记得在IDE环境的配置里添加相应的搜索路径。启用硬件浮点运算单元。开启有关宏定义。【宏开关不用特别去记，缺少的话编译时会报错】

' I$ d* E( I6 w( H) }
; Y* s- A3 S: a9 R- O
- k: j) w% Y9 Z' K
/ f, o" w9 T7 A
下面构造三个矩阵，A矩阵的数据表示某家芯片代理商为他的8个客户分别提供四种不同规格的芯片，数据以包为单位。不同型号的包装规格不一样。A矩阵为8X4矩阵。


, L7 ^4 H' l; V* N# LB矩阵表示A矩阵中各类包装每包的数量、价格、运费、重量，为4X4矩阵。

: x5 Q) J5 _) v
0 H: L' J' X7 u, d/ p& L二者的矩阵乘积表示各个收货方收到芯片的总数、应付货款、运费、以及货物总重量，将构成8X4矩阵。矩阵里的数据使用浮点数，数据随意设计的。
* L! v: Y) U7 }( X/ U! ^
我们知道，两个矩阵可乘有个前提，比方A*B，矩阵A的列数应该等于矩阵B的行数，相乘后所得的乘积矩阵的行数等于矩阵A的行数，其列数等于矩阵B的列数。

# r3 U3 X# s9 g
具体到这里，矩阵A的行数为8，列数为4，矩阵B的行数、列数均为4。A*B所得矩阵的行数为8，列数为4.
7 e8 V- d. ~2 P. I$ M

) q; m. y7 z6 g& a  ?' f; Y1 T4 w) d




, Q. f8 v0 P3 s
下面做相关代码的准备。


& Z2 q) D/ }+ P1 X定义三个数组，pDataA[32]数组对应矩阵A, pDataB[16]数组对应矩阵B,第3个数组pDataC[32]对应矩阵AB乘积所得的新矩阵。

! `; c7 c1 B6 A7 s1 T( Z# U


6 f! X# v4 f3 Z+ f: v. L
8 M4 d  x$ F6 K5 ?( d基于上面的3个数组定义3个如下矩阵变量：

! C4 }& }6 L0 ?+ y# ~- x5 ~# E
  |4 j/ F' e8 ~" J! ]1 {) C% t

$ d2 f/ [0 M% E1 J  L* x
3 L3 ]: |% w/ z5 h1 R( U关于结构体arm_matrix_instance_f32的定义和说明，可以在arm_math.h中看到。
' W& f8 S8 s  |- D( e0 r! M




% z4 `0 v. y% ~$ V* {; g接下来对3个矩阵进行初始化，注意行、列数别给错了。

- q9 p  c' j0 A# G# b+ E$ |( x
. g0 j3 S- ?, u. V/ G5 }( Q9 F
. j/ {% q# `7 @

一切都准备好了，就可以进行矩阵乘法计算了，调用库函数中arm_mat_mult_f32()函数。





矩阵相乘后的运算结果存放在数组pDataC[32]里面，按8*4的矩阵摆放。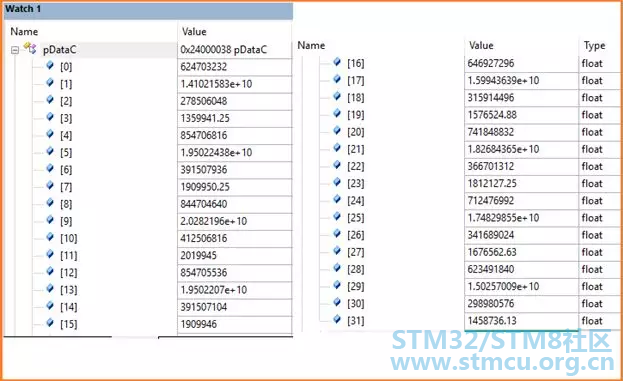

9 f% Q0 @) L) W' [" X) K& B5 i
8 E, [, t% y- c  a! ~8 U
/ i" V9 _/ a. C  L  P
% k! R* p3 a" \% x  P' K
上述运算结果跟使用MATLAB数学工具通过矩阵乘法得到的结果整体上非常一致。数据会稍有些小出入，毕竟是基于浮点运算所得结果。

我们知道，STM32H7是带Cache和FPU的。不妨基于该矩阵乘法应用比较不同情况下的运行时间。以定时器的计数时钟为单位。根据Cache和FPU的开启与关闭的不同组合进行测试,可以做些相对比较，让我们有些直观的感受。测试时ARM MDK的优化等级为-o3。顺便提醒下，如果不开启硬件FPU，调用的DSP库函数应选择另外一个不支持硬件浮点单元的函数库。
1 l4 B! a8 L; T



: t6 [4 S2 {# w7 B+ L) Y" c# U3 l# m
下面数据是基于上面测试代码所得到的，其中红色数据为十进制数据。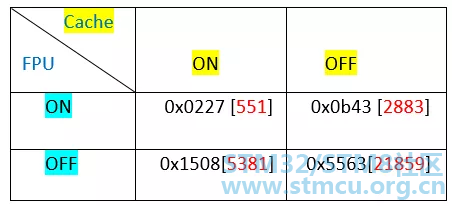
* ?2 ^( l3 c& g) \! N, }" z, V: E
9 }9 B! S* `- H. q! {6 M7 q, c

0 b! Q3 c$ g, A7 \; K6 f3 X
1 j5 K2 I' x% [: i; v4 H
8 w  p" f+ J3 r* \从这里我们可以看出，同时开启硬件FPU和Cache与同时关闭二者，运行时间相差将近40倍；开启Cache与关闭Cache运行时间上相差4倍左右；使用FPU和不用FPU，运行时间相差8倍左右。当然，或许基于不同的应用，上述数据可能存在些差异，但可以肯定，开与不开Cache、启不启用硬件FPU，运行速度上的差别还是很明显的。
) [8 L8 {1 i  n) I3 a- o

好，关于利用STM32及相关DSP函数库进行矩阵运算的演示就介绍到这里，请留意上文中谈到的那些提醒。其它更多细节，有兴趣的话可以进一步阅读和研究相关资料。