STM32的ADC配合DMA采样以及STM32利用DSP库实现快速傅里叶变换，而当二者真正的结合到一起实现一个信号采样以及频域分析才可以发挥出很强大的功能。
# ]: }0 _" T& K1 R0 w
本期我们就来演示，利用DMA+ADC+FFT实现信号采集与频域分析。

# B4 O2 T% v/ c* u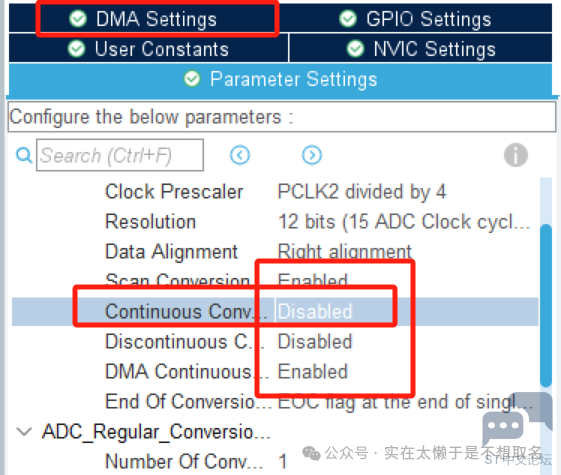) gCUBEMX配置
. p; X9 w4 ^$ j2 C9 }& `8 E3 `
7 j" W% V, Q5 {; I3 G: G

2 z: @+ a7 D% g1 JADC配置这边除了之前的配置之外有一点区别，就是我们把循环采样给关掉，因为我们打算利用定时器来触发采样，这样子的话可以精准的控制采样率。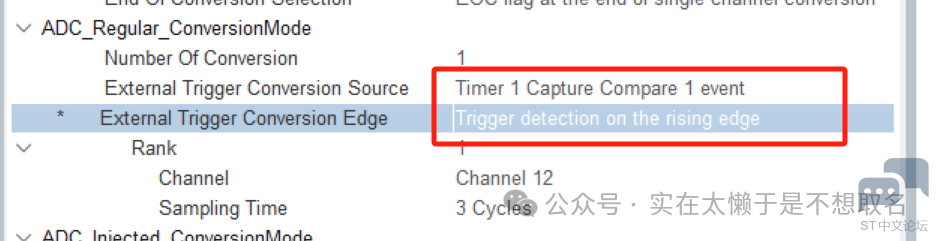

$ }, f8 w) n8 S+ [- w

这里我们选用TIM1的输入捕获来触发，当TIM1输出PWM波的时候，会选取上升沿来触发ADC采样，将采样的数据存储到DMA中。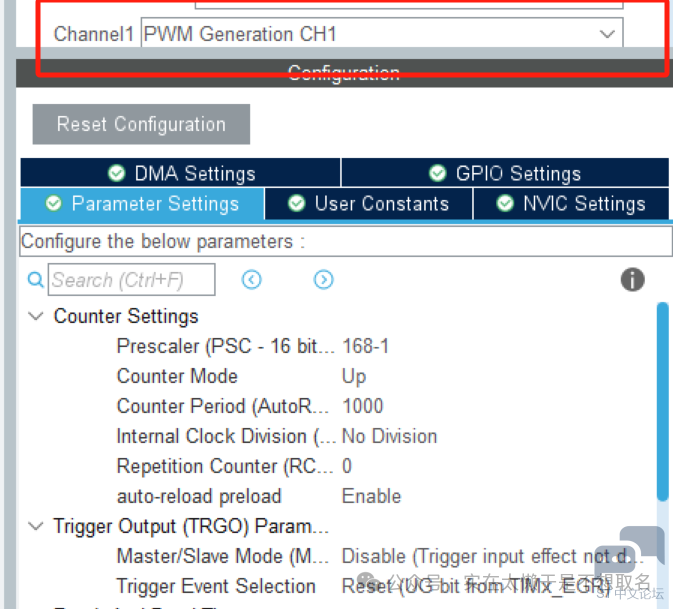
- X( i; h- r+ M4 j  V! e- e, I


+ r; q9 R" ]1 {; y2 P6 Q6 o定时器中我们设置PWM的频率为500HZ,这代表着我们的采样率为500HZ，之后生成我们的代码。（这里非常奇怪，我明明觉得这么算好像是1000HZ但实际只有500HZ，我哪里算错了？）

代码编写

1. #define FFT_LENGTH 1024//采样长度
   2 d1 i; N( F. Q7 N4 |+ u( X
2. arm_cfft_radix4_instance_f32 scfft;//定义scfft结构体
   
3. float FFT_InputBuf[FFT_LENGTH*2];  //FFT输入数组
   ) G3 U& u! n  D0 R
4. float FFT_OutputBuf[FFT_LENGTH];  //FFT输出数组
   0 x; U! Q1 B; W; I
5. uint16_t AD_Value[1024] = {0};//存放ADC的值

复制代码

' [6 w3 X% M% N+ v1 U' r上述代码需要定义在全局，否则可能会因为栈溢出（因为临时变量的定义是存放在栈中的）导致代码崩溃。

1.   HAL_TIM_PWM_Start(&htim1, TIM_CHANNEL_1);        //用来触发adc采样
   4 Q7 q( p2 ]! F
2.   HAL_ADC_Start_DMA(&hadc1, (uint32_t *)AD_Value, FFT_LENGTH);//开启ADC
   1 O+ O$ K' m1 V
3.   arm_cfft_radix4_init_f32(&scfft, FFT_LENGTH,0,1);
   
4.   HAL_Delay(1000);//稍微等待一会ADC一轮转换结束
   
5.     for(int i=0; i < FFT_LENGTH; i++)
   * f) L7 ]+ Y% A3 i0 f" L8 U
6.     {
   6 }0 B& E; }* P
7.       FFT_InputBuf[2*i]=AD_Value[i]*3.3/4096; //实部
   
8.       FFT_InputBuf[2*i+1]=0;          //虚部
   
9.     }
   
10.     arm_cfft_radix4_f32(&scfft,FFT_InputBuf);  
    - B. k" \/ q, M* G
11.     //arm_cmplx_mag_f32(FFT_InputBuf,FFT_OutputBuf,FFT_LENGTH);  //取模得幅值
    
12.     for(int i = 0;i<FFT_LENGTH;i++)
    
13.     {
    
14.       float32_t real = FFT_InputBuf[2 * i];
    
15.        float32_t imag = FFT_InputBuf[2 * i + 1];
    
16.         float32_t magnitude = sqrtf(real * real + imag * imag);
    9 z: }; n% Z" ~9 M
17.         
    4 ~! l' l' |! C$ @! w3 B3 e) j. O7 _
18.         // 打印每个频率分量的模值
    
19.         printf("Fre: %f \r\n", magnitude);
    
20.     }

复制代码

6 k+ j; b8 k4 H2 T* f' L0 M生成代码，我们由定时器触发采样，原始信号来自于一个250HZ的方波。

1 Q% a8 O3 I) r1 B

. Q! }7 L( p: V: G9 R之后我们执行我们的FFT代码，首先我们先看一下采集的波形。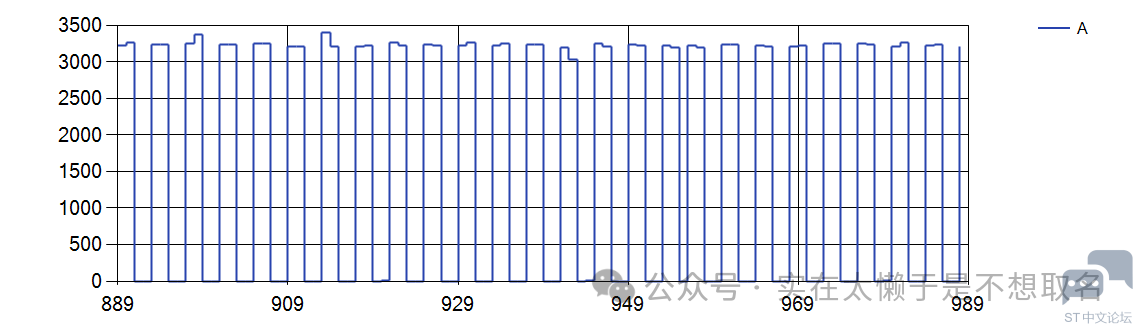
* I' O# i# I& _, t% F+ H% _6 M4 m


这里可以看到外面采集的方波。
& g$ ^% Q# v( ]4 P
注意事项
（这里我的问题，根据奈奎斯特采样定理，采样频率应该至少是信号频率的两倍，否则会出现采样失真，因此为了能够顺利的采样，我将PWM的频率修改为100HZ）



这里也非常奇怪，我觉得PWM的频率应该是100HZ的，但是不知道为什么测出来是50HZ（难不成我又算错了？）

后来发现是我的分时系数算错啦~

; r# Y, P; h* [. c& f" r# C) n变换结果
然后来看看傅里叶变换之后的结果。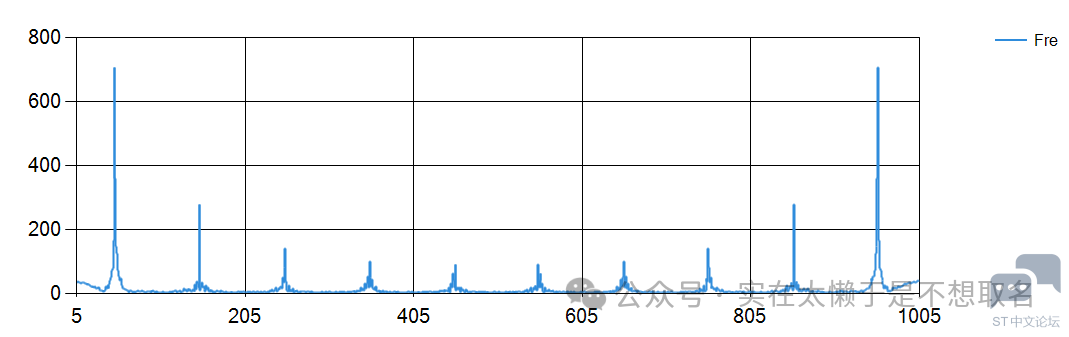
* Y% G, N; D+ |+ ^* q9 t

6 h0 s4 f; T  U4 Y# Q
0 p6 B6 ?; c6 H4 b8 W/ n（这个软件是我自己写的串口示波器）

* X  F+ k' E- s( J! T每个FFT点对应的频率（f）与采样频率（Fs）和FFT的点数（N）之间的关系可以用以下的数学公式表示：
f = k × (Fs / N)
1 x2 k& K1 Q9 U9 t; g' r
其中，k 是FFT结果的索引（从0到N-1），Fs是采样频率，N是FFT的点数（与采样点数相同）。
, a4 ]! T9 e' p7 @9 {( X
2 \" J# _, f* \4 B这里外设定的采样长度是1024，采样频率是500HZ，因此每个点之间的频率差是500/1024（这里按理来说1000更加方便计算但是不知道为什么1000就会卡死，1024就不会，这个也等我研究一下）。

然后用Vofa+来算一下频率（自己的串口示波器不能显示下标，真是失败，我这两天就加上去这个功能）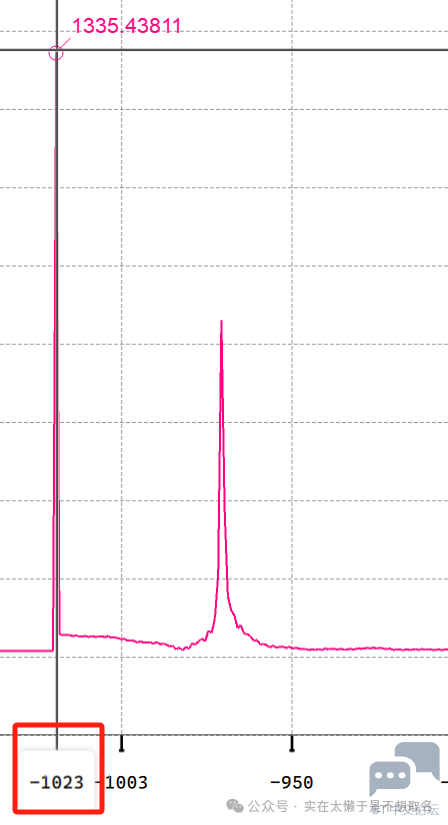
3 M# F9 P5 b+ h! D5 H


首先是开始的这个大信号，毫无疑问就是是直流信号（低频）所带来的幅度。

1 J) L% z/ ^. Q4 G3 \. Y. |2 o这里我给数据加一个直流滤波，就可以把这个很大的直流量给滤掉了。

1.   for(int i = 0;i<FFT_LENGTH;i++)
   8 {( G6 C5 Z) @7 ^9 K$ r
2.   {
   
3.     sum+=AD_Value[i];
   
4.   }
   
5.   sum/=1024;
   
6.     for(int i=0; i < FFT_LENGTH; i++)
   
7.     {
   
8.       FFT_InputBuf[2*i]=(AD_Value[i]-sum)*3.3/4096; //实部
   
9.       FFT_InputBuf[2*i+1]=0;          //虚部
   
10.     }

复制代码

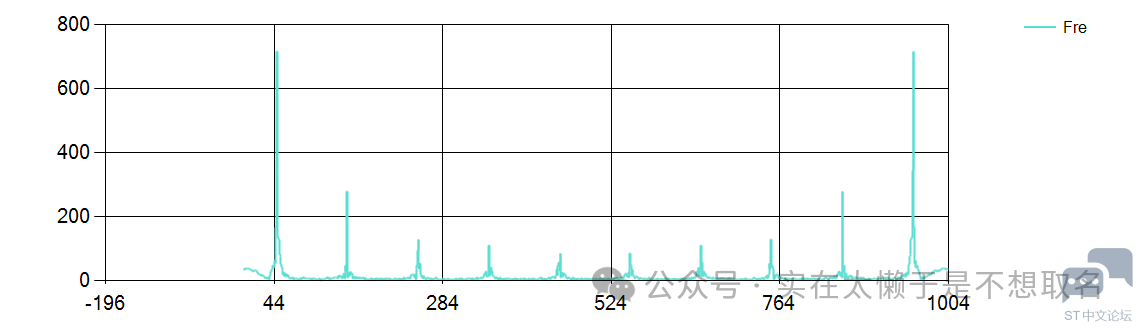
4 u, m, l" r5 @+ z5 X从图中也可以看到，FFT的结果不是一个单边频谱，而是一个双边频谱。
" {% T( n2 X# F; g9 L2 C, H& J$ v# x
3 E8 ?/ k2 u  |3 x- n+ AFFT（快速傅里叶变换）的结果默认是双边频谱，这主要是因为FFT是一种处理复数信号的方法，而复数信号在频域中既有正频率分量也有负频率分量。即使你输入的是实数信号，FFT算法也会将其视为复数信号来处理，并返回包括正频率和负频率在内的双边频谱。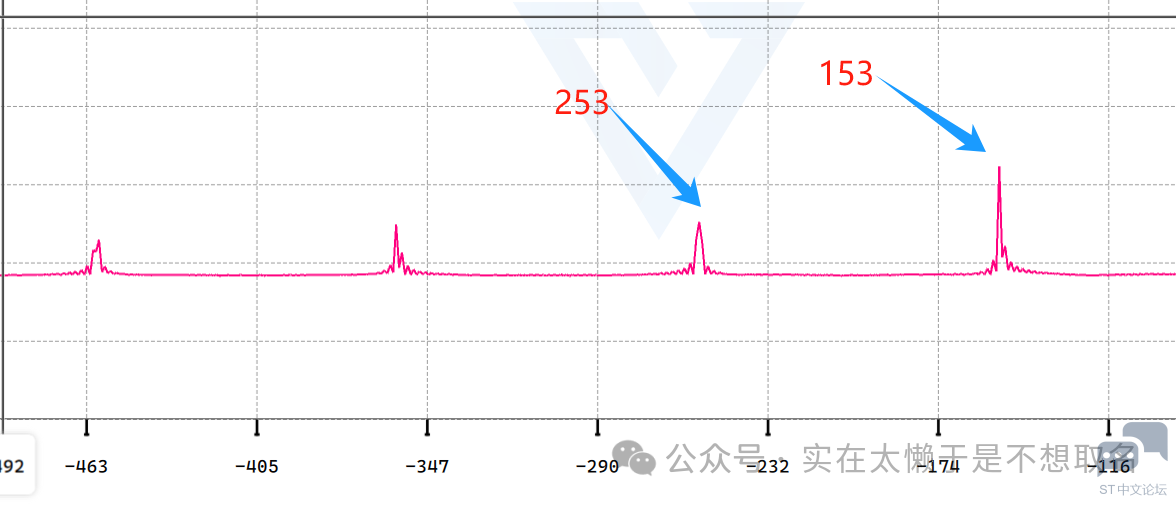
& C+ \, Y+ C4 N* w% |# V" z
$ ^$ Q; ^  B' h/ ~" z$ D; `
: N) R; i; w8 t$ Z9 Y: k
两个峰值之间相差100个点，也就是存在50HZ的倍数波。
/ X2 ]% A1 H, ~0 u

" z$ l# ^" p/ L; c& X
3 C0 p- B: l! v6 u! D# C& W. p3 z这是因为方波是由它的基波频率以及高次谐波所组成。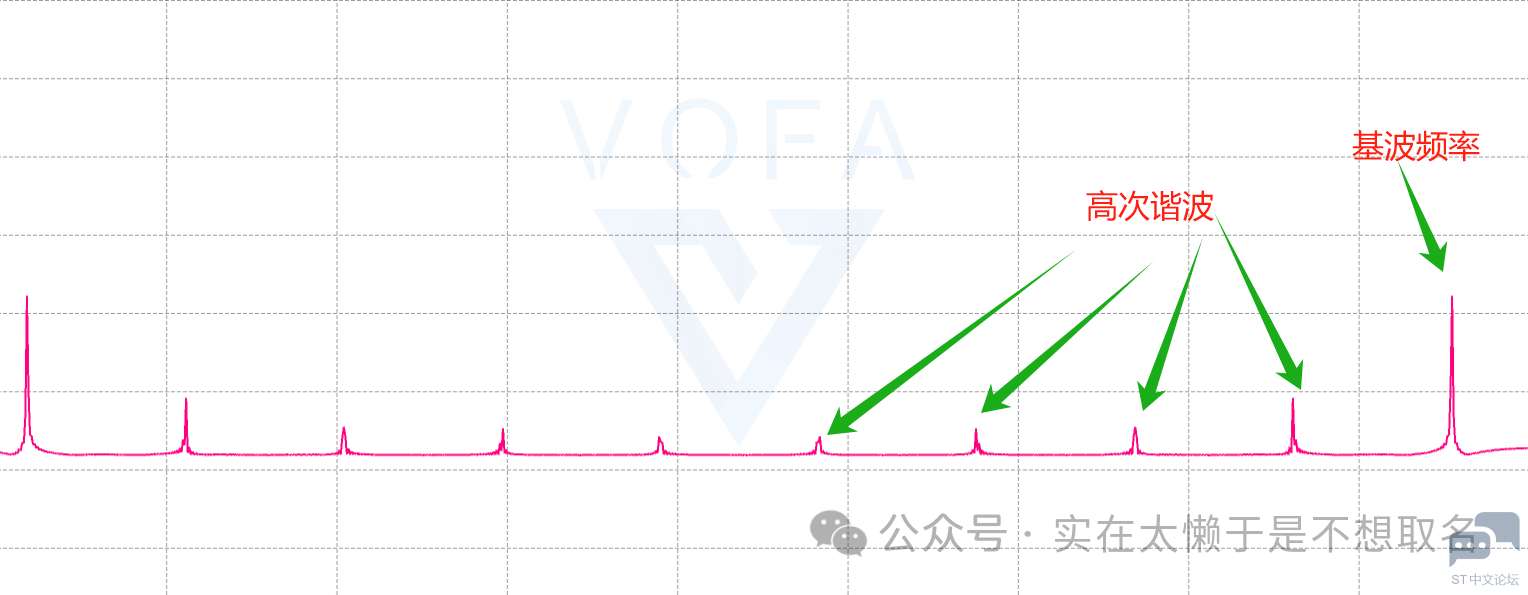
9 @, K! w* P# x  t
! ~: F9 R$ P) g  R) N) U# h

% w2 ~% {& [- i
& E7 G6 l1 x1 s

! i2 K! a* O  S; f转载自：电路小白
如有侵权请联系删除

8 C8 S  r8 g3 w: O. `1 n6 {! w/ Z
- |0 w1 \8 Q; ]4 `9 q

学习学习，正好需要FFT频谱分析