目的和益处
本设计建议阐释了如何分析和识别 MEMS 传感器中的噪声。解释了 Allan 和 Hadamard 方差及其变体（重叠、修正和总体）。还提到了理论方差#1（Theo1）。
优势：
如何通过 Allan 和其他方差来表征 MEMS 传感器
信号和噪声
基本假设是：测量期间目标信号是恒定且平稳的。但是传感器输出是目标信号和噪声的总和。大体上，从长期看噪声应该平均为零。
测量期间采集多个样本。噪声的分析和识别可以帮助确定要使传感器输出的方差最小，需要对 多少个样本取平均。
标准方差的问题在于，它不能很好地表征增加数据运行长度时的情形。为了解决此问题，开发出了 Allan 方差。Allan 方差 σ2被计算为连续“样本”（2 样本方差）之间的平方差的平均值。
通过在时间间隔 τ = m*Ts 中对 m 个样本求平均来计算“样本”，其中 Ts=1/Fs 是采样间隔，Fs 是采样频率。


Allan 方差等等
Allan 偏差 σ(τ)是 Allan 方差 σ2(τ)的平方根。对数-对数图的斜率取决于噪声类型。该斜率能够识别噪声类型。参见下表。
可以使用数字滤波器链来计算 Allan 方差（非重叠 AVAR，重叠 OAVAR，修正 MAVAR）和Hadamard 方差（非重叠 HVAR 和重叠 OHVAR）：
M(m)是 m 个样本的移动平均值，
D1(m)是第 n 个样本与第(n+m+1) 个样本之间的一阶差，
m：通过从 m 个样本中选择 1 个样本进行 1 次下采样

瞬态不得出现在输出中。通过对输出样本求平方和求平均来计算方差。偏差是方差的平方根。可以将偏差的置信度估计为偏差本身除以平均输出样本数的平方根。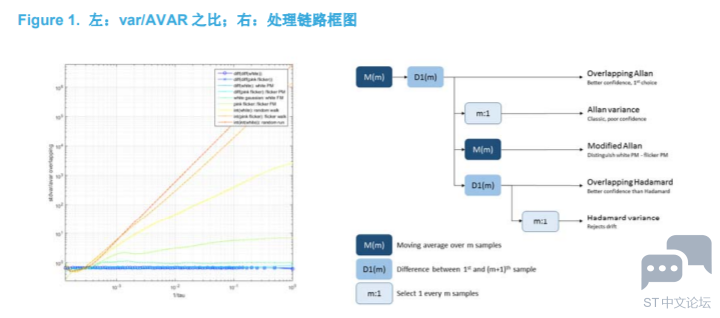





一些重要说明：
重叠 Allan（OAVAR）和重叠 Hadamard 方差（OHVAR）具有更好的置信度，应该用于 m = 10%的数据运行长度情况下。
时间方差（TVAR）是修正 Allan 方差（MAVAR）的缩放版本，缩放因子是 τ2/3。对于白相位噪声它是最佳的（这意味着：白高斯噪声的导数，称为白频噪声）。
Allan 总体、修正总体和 Hadamard 总体方差在 m = 30-50%的数据运行长度时具有更好的置信度。通过在两侧反射来扩展数据运行长度，以此来计算总体方差。对于Allan，反射样本数量为 2m，对于修正 Allan 和 Hadamard，反应样本数量为 3m。
理论#1 方差（Theo1）在 m = 75%的数据运行长度下具有更好的置信度。对于所有其他方差，步幅时间与用于计算“样本”的平均时间相同，var(τ=m*Ts)。对于 Theo1，步幅时间是 m*Ts 减去平均时间；平均时间从 m/2 下降到 1；步幅时间从 m/2 降到m-1；平均步幅时间为 0.75*m*Ts：Theo1(τ=0.75*m*Ts)。Theo1 有偏差，Theo1BR（去除偏差）是无偏的，m <10%时 Theo1H 是 Allan，而 m> 10%时是Theo1BR。

用来计算方差的 MatLab 代码
这是将上述方差计算为数字滤波器链的参考 MatLab 代码。

% Allan 作为一个数字滤波器
n % 平均因子，平均 n 个样本
Fs % 采样频率
Ts=1/Ts;
tau=n*Ts;

%---- STDVAR 和 OSTDVAR
Mn=ones(1,n)/n; % 平均滤波器
dataM=filter(Mn,1,data); dataM=dataM(n:end); % 滤波并去除瞬态
ostdvar()=var(dataM);
stdvar()=var(dataM(1:n:end));


%---- AVAR 和 OAVAR
D1n=zeros(1,n+1); D1n(1)=+1; D1n(end)=-1; % 差分滤波器
dataMD=filter(D1n,1,dataM); dataMD=dataMD(n+1:end); % 滤波并去除瞬态
L=length(dataMD); oavar()=0.5*sum(dataMD.^2)/(L);
L=length(dataMD(1:n:end)); avar()=0.5*sum(dataMD(1:n:end).^2)/(L);


%---- MAVAR
dataMDM=filter(Mn,1,dataMD);
dataMDM=dataMDM(n:end);
L=length(dataMDM); mavar()=0.5*sum(dataMDM.^2)/(L);


%---- HVAR 和 OHVAR
dataMDD=filter(D1n,1,dataMD); dataMDD=dataMDD(n+1:end); % 滤波并去除瞬态
L=length(dataMDD); ohvar()=0.5*sum(dataMDD.^2)/(L);
L=length(dataMDD(1:n:end)); hvar()=0.5*sum(dataMDD(1:n:end).^2)/(L);

上述代码中最慢的一行是移动平均滤波器。如果在添加新项的同时丢弃旧项并保持运行总量不变，则执行速度会快很多。
% OAVAR 最优化
n2=n*n;
acc(1)=sum(data(1:n)); % 初始化运行总数
for i=1:N-n, acc(i+1)=acc(i)-data(i)+data(i+n); end; % 运行总数
oavar()=0.5*sum( (acc(1:N-2*n+1) - acc(1+n:N-n+1)).^2 )/(N-2*n+1)/n2;


% AVAR
diffL=fix((N-2*n+1 -1)/n)+1;
avar()=0.5*sum( (acc(1:n:N-2*n+1)-acc(1+n:n:N-n+1)).^2 )/(diffL)/n2;


% STDVAR 和 OSTDVAR
stdvar()=var(acc(1:n:N-n+1))/n2;
ostdvar()=var(acc(1:N-n+1))/n2;


% MAVAR 最优化
n4=n2*n2;
acc2(1)=sum(acc(1:n)); % 初始化运行总数
for i=1:N-2*n+1, acc2(i+1)=acc2(i)-acc(i)+acc(i+n); end; % 运行总数
mavar()=0.5*sum( (acc2(1:N-3*n+2) - acc2(1+n:N-2*n+2)).^2 )/(N-3*n+2)/n4;


% OHVAR
ohvar()=0.5*sum( ( (acc(1 :N-3*n+1) - acc(1+ n:N-2*n+1)) - ...
(acc(1+n:N-2*n+1) - acc(1+2*n:N- n+1)) ).^2 )/(N-3*n+1)/n2;


% HVAR
diffL=fix((N-3*n+1 -1)/n)+1;
hvar()=0.5*sum( ( (acc(1 :n:N-3*n+1) - acc(1+ n:n:N-2*n+1)) - ...
(acc(1+n:n:N-2*n+1) - acc(1+2*n:n:N- n+1)) ).^2 )/(diffL)/n2;
代码可以进一步优化。例如，对于优化的 C 代码，有可能计算一次得出方差（但通常需要两次计算：第一次用于求均值，第二次用来求实际方差）。

完整版请查看：附件