尝试制作这个四旋翼飞控的过程，感触颇多，整理了思绪之后，把重要的点一一记下来；

这个飞控是基于STM32，整合了MPU6050，即陀螺仪和重力加速计，但没有融合电子罗盘；

另外，四旋翼飞行器的运动方式请百度百科，不太复杂，具体不再赘述；

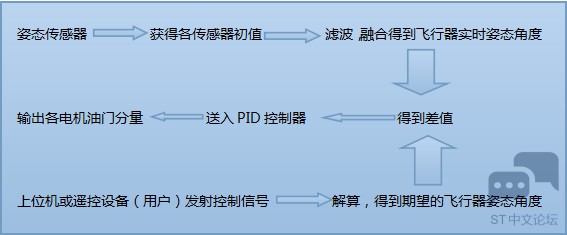
这是飞控程序的控制流程（一个执行周期）：

比较重要的地方：

1.i2c通信方式；

　　因为我不是学电类专业，最开始对i2c这些是没有一点概念，最后通过Google了解了一些原理，然后发现STM32的开发库是带有i2c通信的相关函数的，但是我最后还是没有用这些函数。

我通过GPIO模拟i2c,这样也能获得mpu6050的数据，虽然代码多了一些，但是比较好的理解i2c的原理。

　　STM32库实现的模拟i2c代码（注释好像因为编码问题跪了）：

1. /*******************************************************************************
   
2. // file                :    i2c_conf.h
   
3. // MCU                : STM32F103VET6
   
4. // IDE                : Keil uVision4
   
5. // date                £º2014.2.28
   
6. *******************************************************************************/
   
7. #include "stm32f10x.h"
   
8. 
   
9. #define   uchar unsigned char
   
10. #define   uint unsigned int
    
11. 
    
12. #define      FALSE 0  
    
13. #define   TRUE  1
    
14. 
    
15. void I2C_GPIO_Config(void);
    
16. void I2C_delay(void);
    
17. void delay5ms(void);
    
18. int I2C_Start(void);
    
19. void I2C_Stop(void);
    
20. void I2C_Ack(void);
    
21. void I2C_NoAck(void);
    
22. int I2C_WaitAck(void);
    
23. void I2C_SendByte(u8 SendByte);
    
24. unsigned char I2C_RadeByte(void);
    
25. int Single_Write(uchar SlaveAddress,uchar REG_Address,uchar REG_data);
    
26. unsigned char Single_Read(unsigned char SlaveAddress,unsigned char REG_Address);

复制代码

1. /*******************************************************************************
   
2. // file                :  i2c_conf.c
   
3. // MCU                : STM32F103VET6
   
4. // IDE                : Keil uVision4
   
5. // date                £º2014.2.28
   
6. *******************************************************************************/
   
7. 
   
8. #include "i2c_conf.h"
   
9. 
   
10. #define SCL_H         GPIOB->BSRR = GPIO_Pin_6      
    
11. #define SCL_L         GPIOB->BRR  = GPIO_Pin_6         
    
12. #define SDA_H         GPIOB->BSRR = GPIO_Pin_7
    
13. #define SDA_L         GPIOB->BRR  = GPIO_Pin_7
    
14. 
    
15. #define SCL_read      GPIOB->IDR  & GPIO_Pin_6        //IDR:¶Ë¿ÚÊäÈë¼Ä´æÆ÷¡£
    
16. #define SDA_read      GPIOB->IDR  & GPIO_Pin_7
    
17. 
    
18.                      
    
19. 
    
20. 
    
21. void I2C_GPIO_Config(void)
    
22. {
    
23.   GPIO_InitTypeDef  GPIO_InitStructure;
    
24. 
    
25.   GPIO_InitStructure.GPIO_Pin =  GPIO_Pin_6;
    
26.   GPIO_InitStructure.GPIO_Speed = GPIO_Speed_50MHz;
    
27.   GPIO_InitStructure.GPIO_Mode = GPIO_Mode_Out_OD;   //¿ªÂ©Êä³öģʽ
    
28.   GPIO_Init(GPIOB, &GPIO_InitStructure);
    
29. 
    
30.   GPIO_InitStructure.GPIO_Pin =  GPIO_Pin_7;
    
31.   GPIO_InitStructure.GPIO_Speed = GPIO_Speed_50MHz;
    
32.   GPIO_InitStructure.GPIO_Mode = GPIO_Mode_Out_OD;
    
33.   GPIO_Init(GPIOB, &GPIO_InitStructure);
    
34. }
    
35. 
    
36. 
    
37. void I2C_delay(void)
    
38. {
    
39.         
    
40.    int i=6; //ÕâÀï¿ÉÒÔÓÅ»¯ËٶȠ   £¬¾­²âÊÔ×îµÍµ½5»¹ÄÜдÈë
    
41.    while(i)
    
42.    {
    
43.      i--;
    
44.    }  
    
45. }
    
46. 
    
47. void delay5ms(void)
    
48. {
    
49.         
    
50.    int i=5000;  
    
51.    while(i)
    
52.    {
    
53.      i--;
    
54.    }  
    
55. }
    
56. 
    
57. 
    
58. int I2C_Start(void)
    
59. {
    
60.     SDA_H;                                            //II2ЭÒé¹æ¶¨±ØÐëÔÚʱÖÓÏßΪµÍµçƽµÄÇ°ÌáÏ£¬²Å¿ÉÒÔÈà Êý¾ÝÏßÐźŸıä
    
61.     SCL_H;
    
62.     I2C_delay();
    
63.    
    
64.     if(!SDA_read)
    
65.         return FALSE;                //SDAÏßΪµÍµçƽÔò×ÜÏßæ,Í˳ö
    
66.     SDA_L;                                
    
67.    
    
68.     I2C_delay();
    
69.    
    
70.     if(SDA_read)
    
71.         return FALSE;                //SDAÏßΪ¸ßµçƽÔò×ÜÏß³ö´í,Í˳ö
    
72.     SDA_L;                                
    
73.    
    
74.     I2C_delay();                    
    
75.    
    
76.     return TRUE;
    
77. }
    
78. 
    
79. 
    
80. 
    
81. void I2C_Stop(void)
    
82. {
    
83.     SCL_L;
    
84.     I2C_delay();
    
85.     SDA_L;
    
86.     I2C_delay();
    
87.    
    
88.     SCL_H;
    
89.     I2C_delay();
    
90.     SDA_H;
    
91.     I2C_delay();
    
92. }
    
93. 
    
94. 
    
95. void I2C_Ack(void)
    
96. {   
    
97.     SCL_L;
    
98.     I2C_delay();
    
99.     SDA_L;
    
100.     I2C_delay();
     
101.     SCL_H;
     
102.     I2C_delay();
     
103.     SCL_L;
     
104.     I2C_delay();
     
105. }   
     
106. 
     
107. 
     
108. void I2C_NoAck(void)
     
109. {   
     
110.     SCL_L;
     
111.     I2C_delay();
     
112.     SDA_H;
     
113.     I2C_delay();
     
114.     SCL_H;
     
115.     I2C_delay();
     
116.     SCL_L;
     
117.     I2C_delay();
     
118. }
     
119. 
     
120. 
     
121. 
     
122. int I2C_WaitAck(void)      //·µ»ØΪ:=1ÓÐACK,  =0ÎÞACK
     
123. {
     
124.     SCL_L;
     
125.     I2C_delay();
     
126.     SDA_H;            
     
127.     I2C_delay();
     
128.     SCL_H;
     
129.     I2C_delay();
     
130.     if(SDA_read)
     
131.     {
     
132.       SCL_L;
     
133.       I2C_delay();
     
134.       return FALSE;
     
135.     }
     
136.     SCL_L;
     
137.     I2C_delay();
     
138.     return TRUE;
     
139. }
     
140. 
     
141. 
     
142. 
     
143. 
     
144. void I2C_SendByte(u8 SendByte) //Êý¾Ý´Ó¸ßλµ½µÍλ//
     
145. {
     
146.     u8 i=8;
     
147.     while(i--)
     
148.     {
     
149.         SCL_L;
     
150.         I2C_delay();
     
151.             
     
152.       if(SendByte&0x80)        // 0x80 = 1000 0000;
     
153.         SDA_H;  
     
154.       else
     
155.         SDA_L;   
     
156.             
     
157.         SendByte<<=1;   // SendByte×óÒÆһλ¡£
     
158.         I2C_delay();
     
159.             
     
160.                 SCL_H;
     
161.         I2C_delay();
     
162.     }
     
163.     SCL_L;
     
164. }  
     
165. 
     
166. 
     
167. 
     
168. 
     
169. unsigned char I2C_RadeByte(void)  //Êý¾Ý´Ó¸ßλµ½µÍλ//
     
170. {
     
171.     u8 i=8;
     
172.     u8 ReceiveByte=0;
     
173. 
     
174.     SDA_H;               
     
175.     while(i--)
     
176.     {
     
177.       ReceiveByte<<=1;      //×óÒÆһ룬
     
178.             
     
179.       SCL_L;
     
180.       I2C_delay();
     
181.             
     
182.             SCL_H;
     
183.       I2C_delay();   
     
184.             
     
185.       if(SDA_read)
     
186.       {
     
187.         ReceiveByte|=0x01; //дÈë
     
188.       }
     
189.     }
     
190.     SCL_L;
     
191.     return ReceiveByte;
     
192. }
     
193. 
     
194. 
     
195. 
     
196. int Single_Write(uchar SlaveAddress,uchar REG_Address,uchar REG_data)            
     
197. {
     
198.       if(!I2C_Start())
     
199.             return FALSE;
     
200.     I2C_SendByte(SlaveAddress);   //·¢ËÍÉ豸µØÖ·+дÐźŠ   //I2C_SendByte(((REG_Address & 0x0700) >>7) | SlaveAddress & 0xFFFE);    //ÉèÖøßÆðʼµØÖ·+Æ÷¼þµØÖ·
     
201.    
     
202.         if(!I2C_WaitAck())
     
203.         {
     
204.             I2C_Stop();
     
205.             return FALSE;
     
206.         }
     
207.    
     
208.         I2C_SendByte(REG_Address );   //ÉèÖõÍÆðʼµØÖ·      
     
209.     I2C_WaitAck();   
     
210.    
     
211.         I2C_SendByte(REG_data);
     
212.     I2C_WaitAck();   
     
213.    
     
214.         I2C_Stop();
     
215.     delay5ms();
     
216.     return TRUE;
     
217. }
     
218. 
     
219. 
     
220. 
     
221. unsigned char Single_Read(unsigned char SlaveAddress,unsigned char REG_Address)
     
222. {   
     
223.     unsigned char REG_data;
     
224. 
     
225.    
     
226.         if(!I2C_Start())
     
227.             return FALSE;
     
228.     I2C_SendByte(SlaveAddress); //I2C_SendByte(((REG_Address & 0x0700) >>7) | REG_Address & 0xFFFE);//ÉèÖøßÆðʼµØÖ·+Æ÷¼þµØÖ·
     
229.     if(!I2C_WaitAck())
     
230.         {
     
231.             I2C_Stop();
     
232. 
     
233.             return FALSE;
     
234.         }
     
235.     I2C_SendByte((u8) REG_Address);   //ÉèÖõÍÆðʼµØÖ·      
     
236.     I2C_WaitAck();
     
237.         I2C_Start();
     
238.    
     
239.         I2C_SendByte(SlaveAddress+1);
     
240.     I2C_WaitAck();
     
241. 
     
242.         REG_data= I2C_RadeByte();
     
243.     I2C_NoAck();
     
244.     I2C_Stop();
     
245. 
     
246.     return REG_data;
     
247. 
     
248. }

复制代码

2.mpu6050;

　　然后用写好的模拟i2c函数读取mpu6050，根据mpu6050手册的各寄存器地址，读取到了重力加速计和陀螺仪的各分量;

传感器采样率设置为200Hz,这个值是因为我电调频率为200Hz，也就是说，我的程序循环一次0.005s,一般来说，采样率高点没问题，别比执行一次闭环控制的周期长就行了；

陀螺仪量程±2000°/s，加速计量程±2g， 量程越大，取值越不精确；

这里注意，由于我们没有采用磁力计，而陀螺仪存在零偏，所以最终在yaw方向上没有绝对的参考系，不能建立绝对的地理坐标系，这样最好的结果也仅仅是在yaw上存在缓慢漂移。

3.互补滤波；

　　融合时，陀螺仪的积分运算很大程度上决定了飞行器的瞬时运动情况，而重力加速计通过长时间的累积不断矫正陀螺仪产生的误差，最终得到准确的机体姿态。

　　这里我们采用Madgwick提供的UpdateIMU算法来得到姿态角所对应的四元数，之后只需要经过简单运算便可转换为实时欧拉角。感谢Madgwick大大为开源做出的贡献。

1. #define sampleFreq    512.0f        // sample frequency in Hz
   
2. #define betaDef        0.1f        // 2 * proportional gain
   
3. 
   
4. 
   
5. volatile float beta = betaDef;
   
6. volatile float q0 = 1.0f, q1 = 0.0f, q2 = 0.0f, q3 = 0.0f;
   
7. 
   
8. float invSqrt(float x);
   
9. 
   
10. void MadgwickAHRSupdateIMU(float gx, float gy, float gz, float ax, float ay, float az) {
    
11.     float recipNorm;
    
12.     float s0, s1, s2, s3;
    
13.     float qDot1, qDot2, qDot3, qDot4;
    
14.     float _2q0, _2q1, _2q2, _2q3, _4q0, _4q1, _4q2 ,_8q1, _8q2, q0q0, q1q1, q2q2, q3q3;
    
15. 
    
16.     // Rate of change of quaternion from gyroscope
    
17.     qDot1 = 0.5f * (-q1 * gx - q2 * gy - q3 * gz);
    
18.     qDot2 = 0.5f * (q0 * gx + q2 * gz - q3 * gy);
    
19.     qDot3 = 0.5f * (q0 * gy - q1 * gz + q3 * gx);
    
20.     qDot4 = 0.5f * (q0 * gz + q1 * gy - q2 * gx);
    
21. 
    
22.     // Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation)
    
23.     if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) {
    
24. 
    
25.         // Normalise accelerometer measurement
    
26.         recipNorm = invSqrt(ax * ax + ay * ay + az * az);
    
27.         ax *= recipNorm;
    
28.         ay *= recipNorm;
    
29.         az *= recipNorm;
    
30. 
    
31.         // Auxiliary variables to avoid repeated arithmetic
    
32.         _2q0 = 2.0f * q0;
    
33.         _2q1 = 2.0f * q1;
    
34.         _2q2 = 2.0f * q2;
    
35.         _2q3 = 2.0f * q3;
    
36.         _4q0 = 4.0f * q0;
    
37.         _4q1 = 4.0f * q1;
    
38.         _4q2 = 4.0f * q2;
    
39.         _8q1 = 8.0f * q1;
    
40.         _8q2 = 8.0f * q2;
    
41.         q0q0 = q0 * q0;
    
42.         q1q1 = q1 * q1;
    
43.         q2q2 = q2 * q2;
    
44.         q3q3 = q3 * q3;
    
45. 
    
46.         // Gradient decent algorithm corrective step
    
47.         s0 = _4q0 * q2q2 + _2q2 * ax + _4q0 * q1q1 - _2q1 * ay;
    
48.         s1 = _4q1 * q3q3 - _2q3 * ax + 4.0f * q0q0 * q1 - _2q0 * ay - _4q1 + _8q1 * q1q1 + _8q1 * q2q2 + _4q1 * az;
    
49.         s2 = 4.0f * q0q0 * q2 + _2q0 * ax + _4q2 * q3q3 - _2q3 * ay - _4q2 + _8q2 * q1q1 + _8q2 * q2q2 + _4q2 * az;
    
50.         s3 = 4.0f * q1q1 * q3 - _2q1 * ax + 4.0f * q2q2 * q3 - _2q2 * ay;
    
51.         recipNorm = invSqrt(s0 * s0 + s1 * s1 + s2 * s2 + s3 * s3); // normalise step magnitude
    
52.         s0 *= recipNorm;
    
53.         s1 *= recipNorm;
    
54.         s2 *= recipNorm;
    
55.         s3 *= recipNorm;
    
56. 
    
57.         // Apply feedback step
    
58.         qDot1 -= beta * s0;
    
59.         qDot2 -= beta * s1;
    
60.         qDot3 -= beta * s2;
    
61.         qDot4 -= beta * s3;
    
62.     }
    
63. 
    
64.     // Integrate rate of change of quaternion to yield quaternion
    
65.     q0 += qDot1 * (1.0f / sampleFreq);
    
66.     q1 += qDot2 * (1.0f / sampleFreq);
    
67.     q2 += qDot3 * (1.0f / sampleFreq);
    
68.     q3 += qDot4 * (1.0f / sampleFreq);
    
69. 
    
70.     // Normalise quaternion
    
71.     recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
    
72.     q0 *= recipNorm;
    
73.     q1 *= recipNorm;
    
74.     q2 *= recipNorm;
    
75.     q3 *= recipNorm;
    
76. }
    
77. 
    
78. 
    
79. float invSqrt(float x) {
    
80.     float halfx = 0.5f * x;
    
81.     float y = x;
    
82.     long i = *(long*)&y;
    
83.     i = 0x5f3759df - (i>>1);
    
84.     y = *(float*)&i;
    
85.     y = y * (1.5f - (halfx * y * y));
    
86.     return y;
    
87. }

复制代码

4.获取期望姿态；

　　也就是遥控部分了，让用户介入控制。

　　本着拿来主义的原则，用上”圆点博士开源项目”提供的安卓的开源蓝牙控制端。

　　圆点博士给出了数据包格式，同过HC-06蓝牙模块接连到STM32串口1，再无线连接到控制端，这样我们就可以获得控制端不断发送的数据包了，并实时更新期望姿态角，这里只需要注意输出的姿态角和实时姿态角方向一致以及数据包的校验就行了。

5.PID控制算法；

　　由于简单的线性控制不可能满足四轴飞行器这个灵敏的系统，引入PID控制器来更好的纠正系统。

　　简介：PID实指“比例proportional”、“积分integral”、“微分derivative”，这三项构成PID基本要素。每一项完成不同任务，对系统功能产生不同的影响。

以Pitch为例：

　　

error为期望角减去实时角度得到的误差；

iState为积分i参数对应累积过去时间里的误差总和；

if语句限定iState范围，繁殖修正过度；

微分d参数为当前姿态减去上次姿态，估算当前速度（瞬间速度）；

总调整量为p,i,d三者之和；

这样，P代表控制系统的响应速度，越大，响应越快。

I，用来累积过去时间内的误差，修正P无法达到的期望姿态值（静差）；

D，加强对机体变化的快速响应，对P有抑制作用。

PID各参数的整定需要综合考虑控制系统的各个方面，才能达到最佳效果。

输出PWM信号：

PID计算完成之后，便可以通过STM32自带的定时资源很容易的调制出四路pwm信号，采用的电调pwm格式为50Hz，高电平持续时间0.5ms-2.5ms；

我以1.0ms-2.0ms为每个电机的油门行程，这样，1ms的宽度均匀的对应电调的从最低到最高转速。

至此，一个用stm32和mpu6050搭建的飞控系统就算实现了。

剩下的调试PID参数了。

转载自：Moran_