
前面介绍过一期在STM32中进行傅里叶变换的教程,我们成功的对一段信号进行了傅里叶变换,获得其频率谱。+ h3 }0 O: ~6 r) J3 j( x![3B_8}BWR[]ZBFD2U~56EA@W.png 3B_8}BWR[]ZBFD2U~56EA@W.png](data/attachment/forum/202405/29/165309ibaavj5bjymklwlj.png)
同样的,我们也同样介绍了双边频谱:FFT的结果是一个双边频谱,他不仅仅包含了实数的频谱也包含了负频率的频谱。 我们的采样长度为FFT_Lenth,同样的傅里叶变换的长度也是FFT_Lenth,而由于双边频谱的存在,我们的FFT结果数组长度是2*FFT_Lenth,并且通常直流信号会被统计两次。 事实上对于我们的时域信号而言,我们采集到的数据仅仅只是实部信号(虚部信号之所以叫做虚部信号也正是因为在复平面上)。 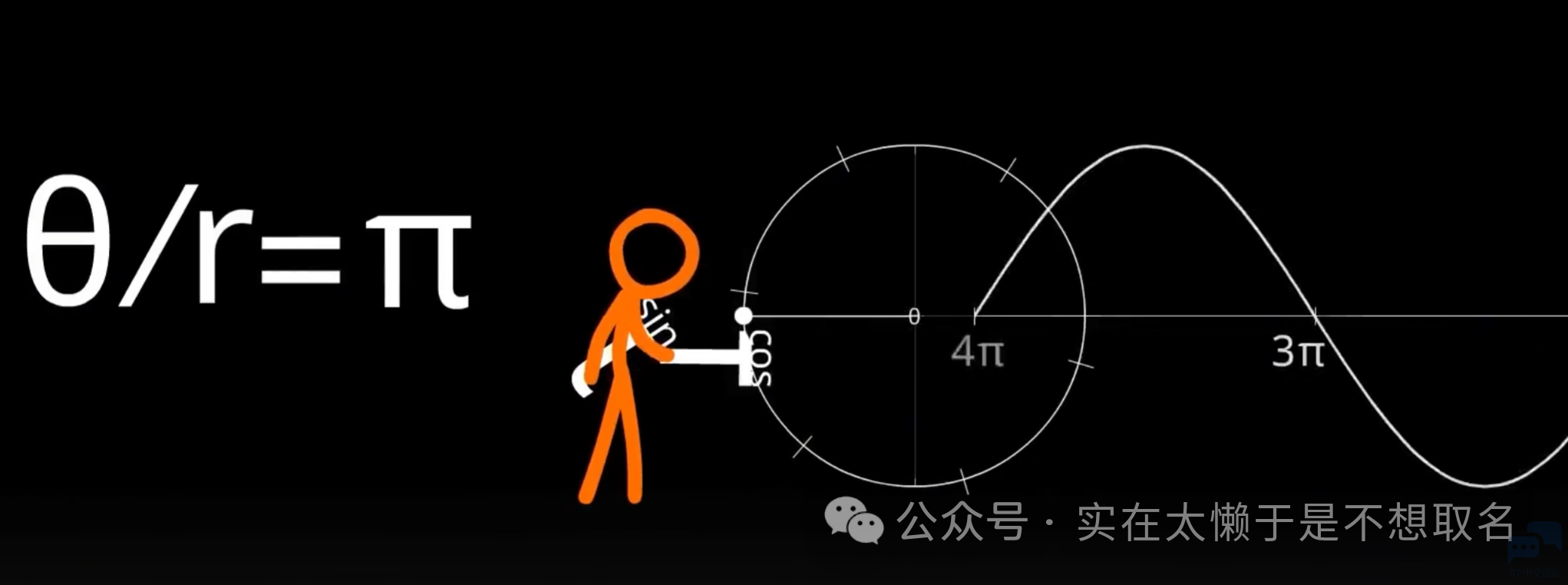
在大名鼎鼎的火柴人数学中也体现了这一点。0 { k/ D" }# p0 b& z- g " m+ L3 { p/ {% v+ E% \ 
; Q5 q% r- `& M1 E+ M 而真正的信号应该是一个在复平面上的合信号,但是对于我们而言虚数轴上并没有什么意义。! P8 m0 L: E; K5 F- q 5 _& M% \8 o l2 l7 z 因此我们在计算FFT的时候也会主动的不向原始信号虚数轴上填充数据。' f7 j8 r, Q& ]2 ~# m" g+ E/ Q
但是,即便是我们主动的忽略了时域信号中的虚部,但是FFT的结果中依旧包含了负频率的双边频谱 + x& T9 U9 b' r5 v 
0 x* E5 s( u5 b3 c J3 @( a 因此,当我们利用得到频谱的时候,通常情况下只考虑他的单边频谱,而负频率通常是不考虑的。 ) C( C/ O8 c+ y+ o8 H, e 好了,说了那么多我们还是聊聊我们接下去要干什么,FFT在STM32中的应用有许多文章都在对其进行介绍,但是几乎没有文章有介绍IFFT也就是傅里叶反变换。 也对,通常我们知道的时域信号,我们通过傅里叶变换之后将其转换为频域信号,但是很少有知道频域的情况下对其进行傅里叶反变换,因为首先是应用场合比较少,其次是好像没什么必要。! _- q& B4 i& {+ q- J 但是如果我们可以实现傅里叶反变换,那能不能通过对其频率信息的修改,即修改频域的值,实现一种滤波效果。 ' X& w! S$ F2 O7 K; Z) ? 假如我们的信号采样率为10KHZ即10240,而我们的FFT长度是1024,那么我们的输出数组结果所对应的频率差,即相邻两个数据对应的频率差为10240/1024 = 10HZ2 @1 A0 t$ K9 [2 [ U7 u' r6 a: `" _3 l 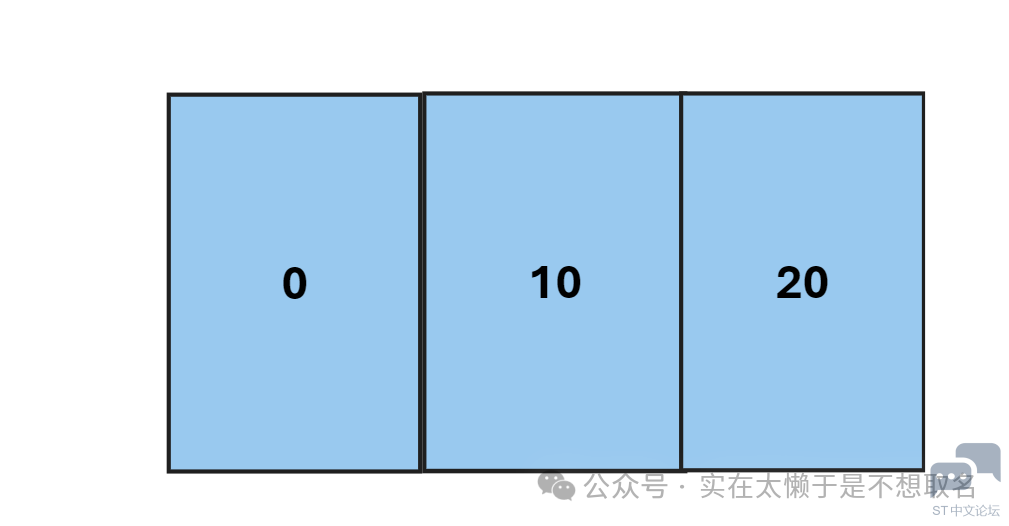
0 J) ~2 d0 h" B 那么例如我们将FFT的结果中前2*X项赋值为0(因为输出的结果中包含了一个实部数据和一个虚部数据)并且FFT_Lenth~FFT_Lenth*2的值均为负频率。 这样子我们就可以实现一个X*10(频率差)的一个高通滤波器(低频段被删除了),之后我们通过傅里叶反变换实现还原原始信号。 ) a5 A0 z2 [$ v9 n2 \8 `& t 这里需要注意的是,DSP库中没有给出IFFT的算法,因此我们选用最常见到的累加法求其IFFT的结果。 $ s+ C9 K# H& M H( K* B
这里不具体介绍原理,总之我们看看效果。1 a6 r4 n; K0 Z! T( k& z9 I4 Z 
将信号采集之后经过FFT变换之后再通过IFFT反变换为时域信号。7 F+ Z! b1 [* f6 H' q3 e & r. R/ X7 z b% x9 p' P 这里我们采集了3KHZ的信号并进行了还原,可以看到并没有什么失真。 
三角波的还原,可以看到似乎叠加了一个什么信号,但是不是很明显。( o% Z/ j4 \: k& I" l . e; a$ p" s, T' T! s+ y& { 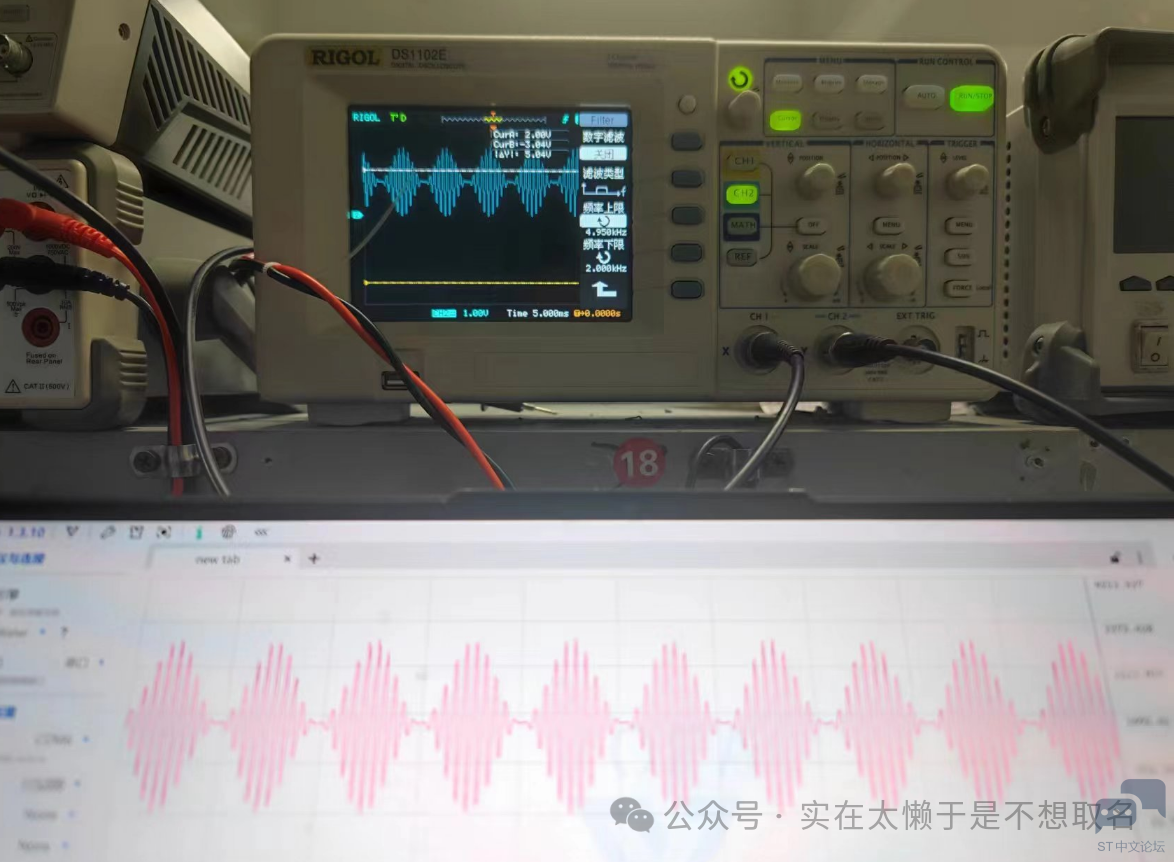
6 k3 C; u7 m4 X/ U6 T' ^+ c 调制信号的还原,可以看到信号还原度还是非常高的。' `# O8 `3 \) c _% g6 p( O& ~ 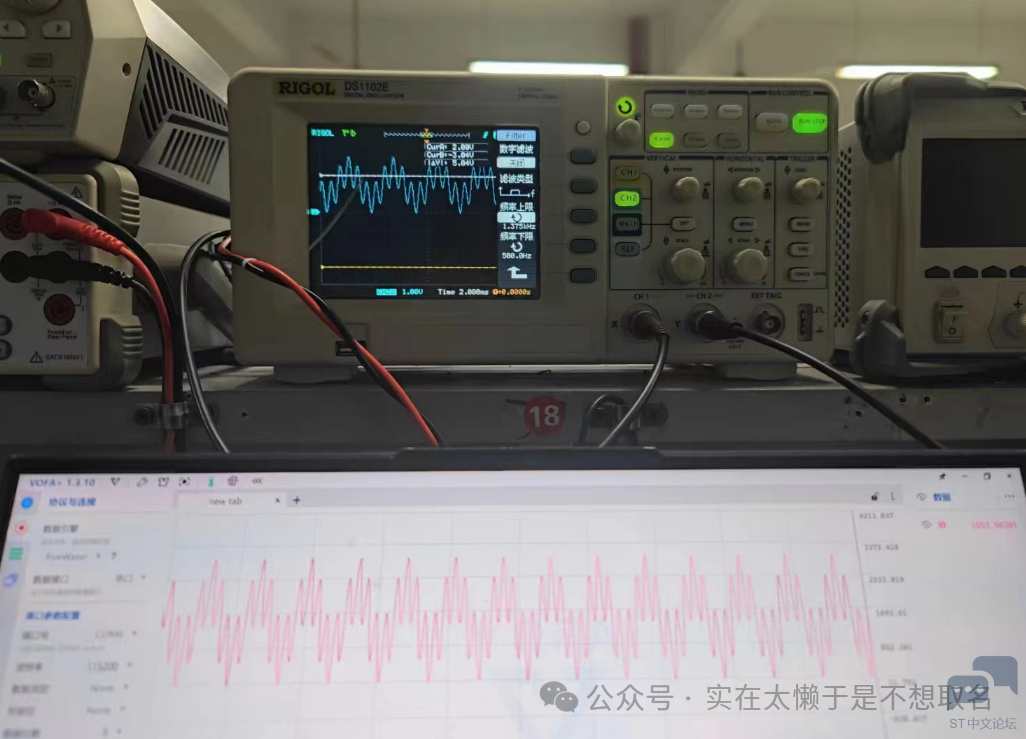
0 b, ?8 R$ c* |' a4 v9 V0 [ V 两个正弦波,100HZ+500HZ的累加信号,可以看到其还原度也是非常高的。0 [6 C0 m9 W, {, j9 G" v) M( J & c6 P% c' ]$ `. g* e9 r) b 在这里我们应用一下我们之前的方法,将某个频段的信号去除。 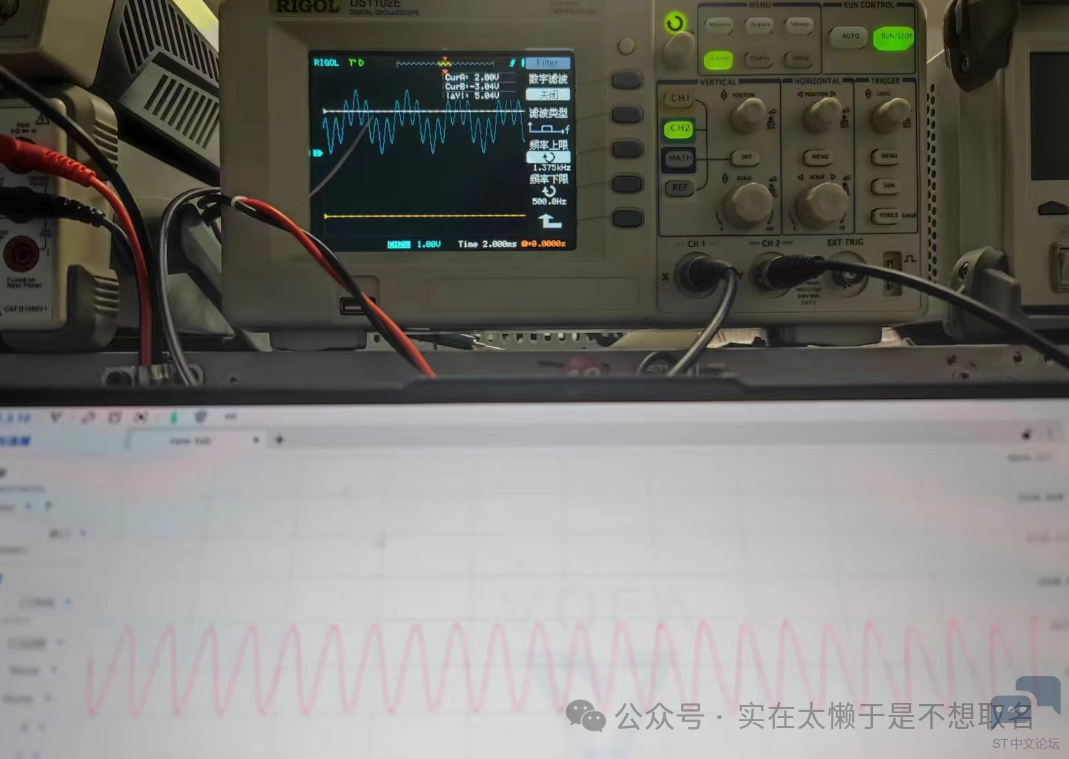
可以看到,我们非常轻松的从500HZ的信号中提取到了100HZ的信号。 3 `, a: V4 }0 l0 n" @: E 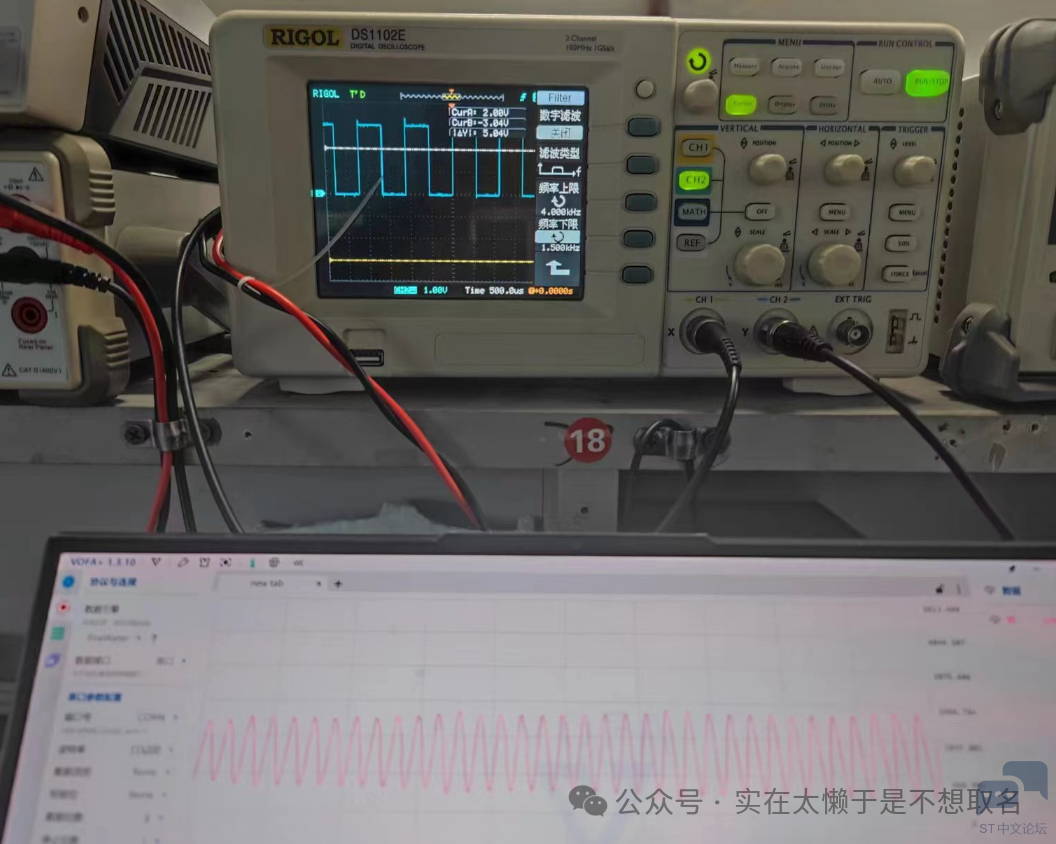
方波中提取其基波频率。6 V/ x( \/ {# p 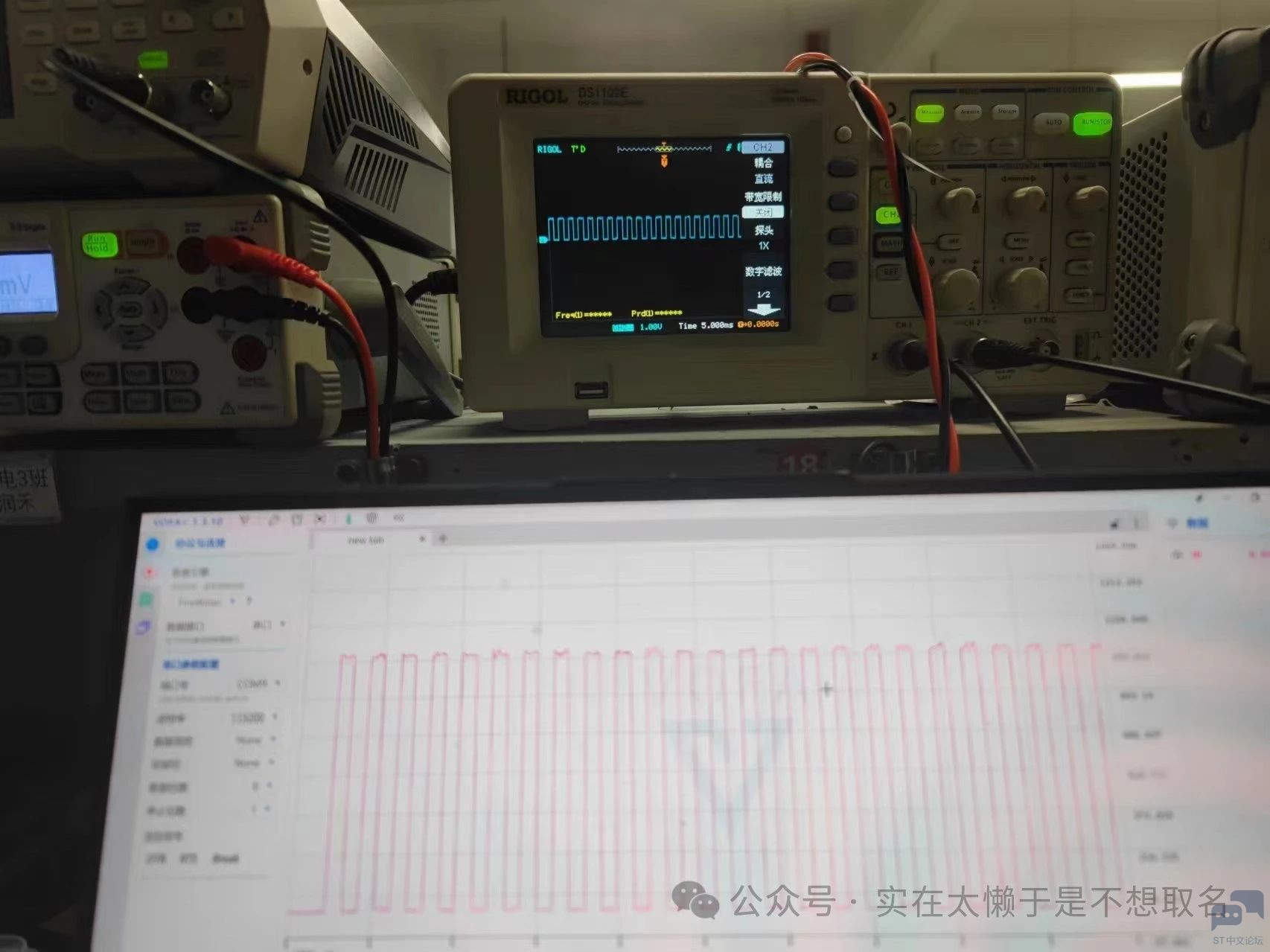
# N, o& K9 P; u# _ 以及还有方波信号的 还原。( U" {$ {" t( a. x & g4 x0 j$ u h1 _, l 并且这个方法 的滤波精度相当之高。 $ l' v9 Z8 M4 P9 x6 ] 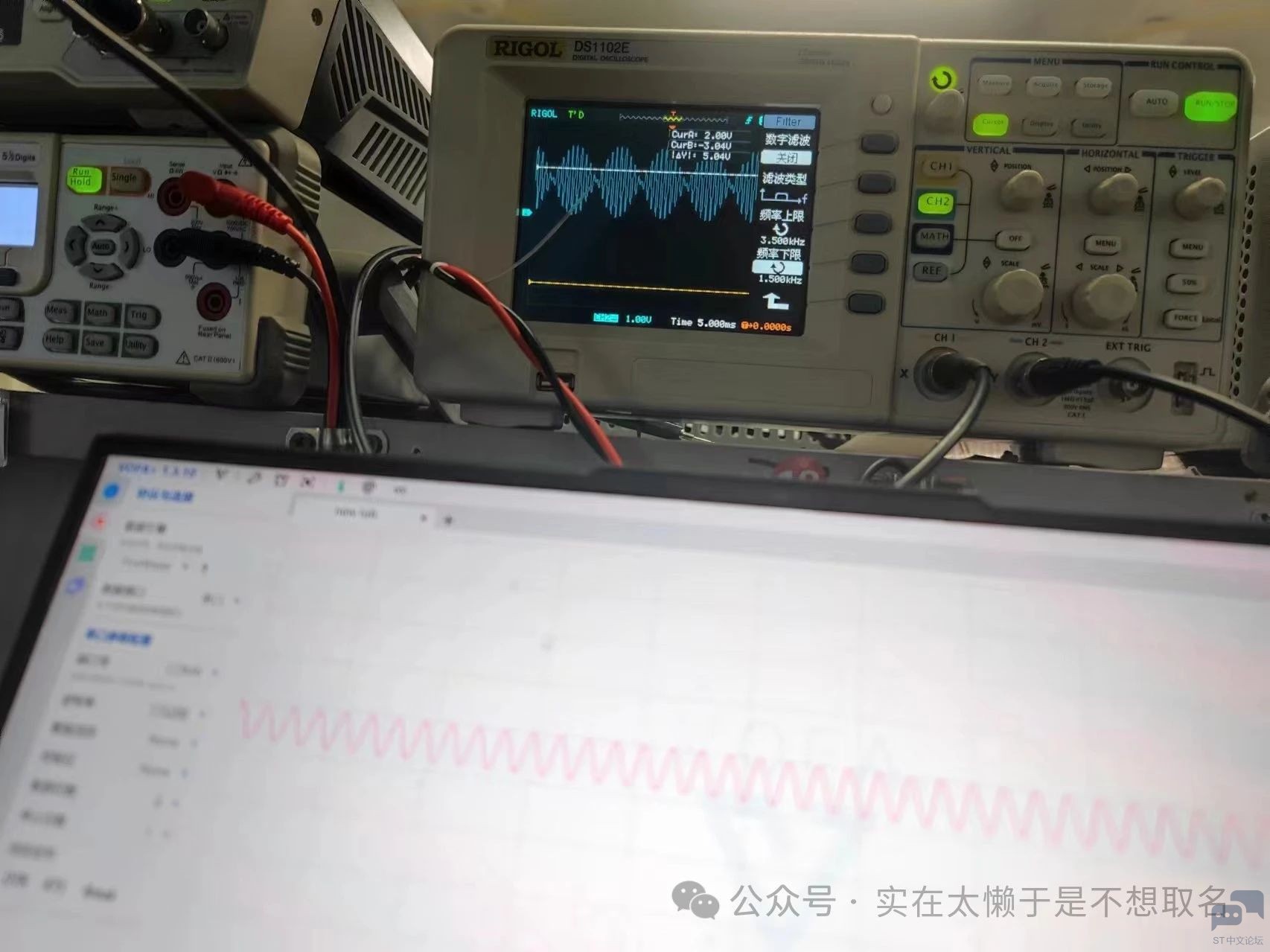
从一个900HZ叠加1000HZ的信号中将1000HZ的分量去掉。4 C+ c8 y) i C# f% n6 c' D" }# S% F 9 l p& M' N) e4 J 1 d5 _9 h) t; x2 C 转载自:电路小白9 D2 k) m" t+ h 如有侵权请联系删除$ _# ]( _+ s: g8 y5 i- h" H # {3 L4 H: s/ j5 U7 R" K) o |
【2025·STM32峰会】GUI解决方案实训分享2-编译运行TouchGFX咖啡机例程(含桌面仿真)
实战经验 | Keil工程使用NEAI库的异常问题
STM32 ISP IQTune:真正零门槛的免费ISP调整软件
【经验分享】STM32 新建基于STM32F40x 固件库的MDK5 工程
意法半导体MCU双供应链策略,打消中国客户后顾之忧
【经验分享】基于STM32使用HAL库实现USB组合设备CDC+MSC
2024意法半导体工业峰会:赋能智能电源和智能工业,构筑可持续未来
ST推出灵活、面向未来的智能电表通信解决方案,助力能源转型
意法半导体 x Qu-Bit Electronix:推动新一轮的数字声音合成革命
从STM32 MPU产品看嵌入式系统中微处理器的新变化
 微信公众号
微信公众号
 手机版
手机版
