前面介绍过一期在STM32中进行傅里叶变换的教程，我们成功的对一段信号进行了傅里叶变换，获得其频率谱。


同样的，我们也同样介绍了双边频谱：FFT的结果是一个双边频谱，他不仅仅包含了实数的频谱也包含了负频率的频谱。

我们的采样长度为FFT_Lenth，同样的傅里叶变换的长度也是FFT_Lenth，而由于双边频谱的存在，我们的FFT结果数组长度是2*FFT_Lenth，并且通常直流信号会被统计两次。

事实上对于我们的时域信号而言，我们采集到的数据仅仅只是实部信号（虚部信号之所以叫做虚部信号也正是因为在复平面上）。



在大名鼎鼎的火柴人数学中也体现了这一点。



而真正的信号应该是一个在复平面上的合信号，但是对于我们而言虚数轴上并没有什么意义。

因此我们在计算FFT的时候也会主动的不向原始信号虚数轴上填充数据。

1.     for(int i=0; i < FFT_LENGTH; i++)
   
2.     {
   
3.       FFT_InputBuf[2*i]=(ADC_1_Value_DMA )*3.3/4096; //实部
   
4.       FFT_InputBuf[2*i+1]=0;          //虚部
   
5.     }

复制代码

但是，即便是我们主动的忽略了时域信号中的虚部，但是FFT的结果中依旧包含了负频率的双边频谱



因此，当我们利用得到频谱的时候，通常情况下只考虑他的单边频谱，而负频率通常是不考虑的。

好了，说了那么多我们还是聊聊我们接下去要干什么，FFT在STM32中的应用有许多文章都在对其进行介绍，但是几乎没有文章有介绍IFFT也就是傅里叶反变换。

也对，通常我们知道的时域信号，我们通过傅里叶变换之后将其转换为频域信号，但是很少有知道频域的情况下对其进行傅里叶反变换，因为首先是应用场合比较少，其次是好像没什么必要。

但是如果我们可以实现傅里叶反变换，那能不能通过对其频率信息的修改，即修改频域的值，实现一种滤波效果。

假如我们的信号采样率为10KHZ即10240，而我们的FFT长度是1024，那么我们的输出数组结果所对应的频率差，即相邻两个数据对应的频率差为10240/1024 = 10HZ



那么例如我们将FFT的结果中前2*X项赋值为0(因为输出的结果中包含了一个实部数据和一个虚部数据)并且FFT_Lenth~FFT_Lenth*2的值均为负频率。

这样子我们就可以实现一个X*10（频率差）的一个高通滤波器（低频段被删除了），之后我们通过傅里叶反变换实现还原原始信号。

这里需要注意的是，DSP库中没有给出IFFT的算法，因此我们选用最常见到的累加法求其IFFT的结果。

1.     for (int i = 0; i < FFT_LENGTH; i++) {  
   
2.     FFT_OutputBuf = 0.0f;   
   
3.     for (int k = 0; k < FFT_LENGTH; k++) {  
   
4.         // 累加复数乘法结果到原始信号  
   
5.         float32_t phase = -2.0f * 3.1415926 * i * k / FFT_LENGTH; // 计算相位  
   
6.         float32_t real_part = cosf(phase) * FFT_InputBuf[2*k] + sinf(phase) * FFT_InputBuf[k*2+1];  
   
7.         //float32_t imag_part = -sinf(phase) * FFT_InputBuf[k*2+0] + cosf(phase) * FFT_InputBuf[k*2+1];虚部信号  
   
8.         FFT_OutputBuf += real_part; // 只取实部累加，因为原始信号是实数  
   
9.     }  
   
10.   
    
11. }

复制代码

这里不具体介绍原理，总之我们看看效果。


将信号采集之后经过FFT变换之后再通过IFFT反变换为时域信号。

这里我们采集了3KHZ的信号并进行了还原，可以看到并没有什么失真。



三角波的还原，可以看到似乎叠加了一个什么信号，但是不是很明显。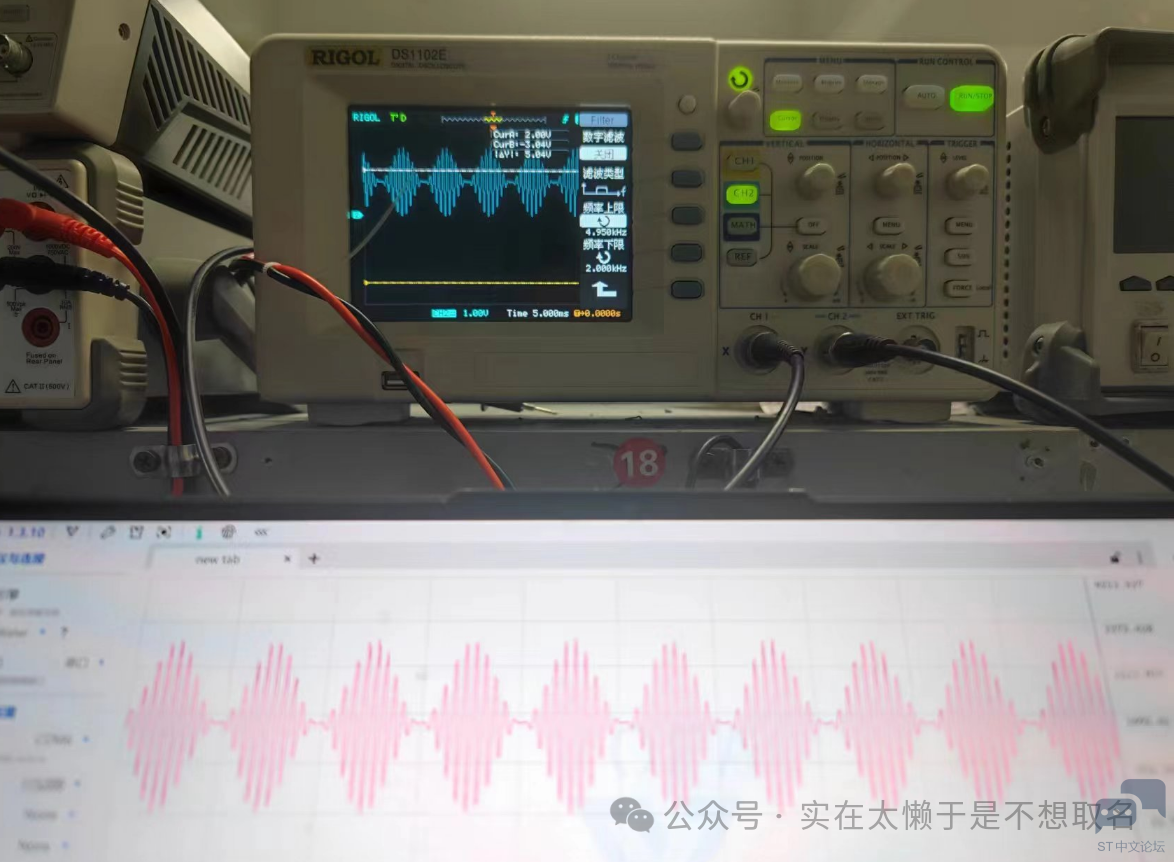



调制信号的还原，可以看到信号还原度还是非常高的。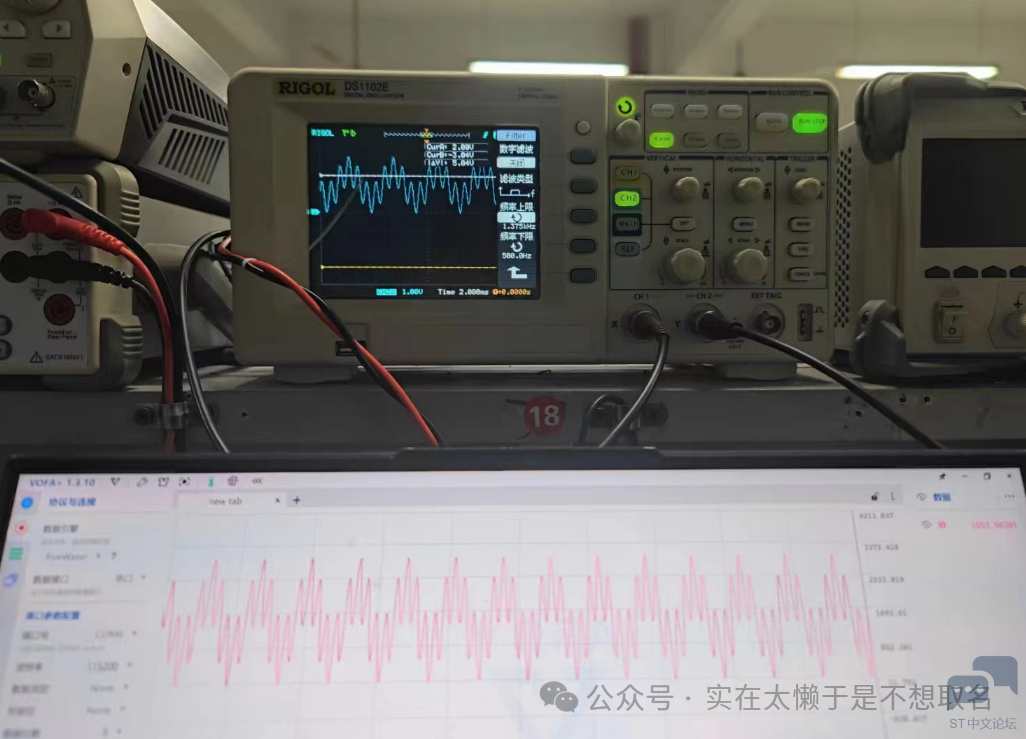



两个正弦波，100HZ+500HZ的累加信号，可以看到其还原度也是非常高的。

在这里我们应用一下我们之前的方法，将某个频段的信号去除。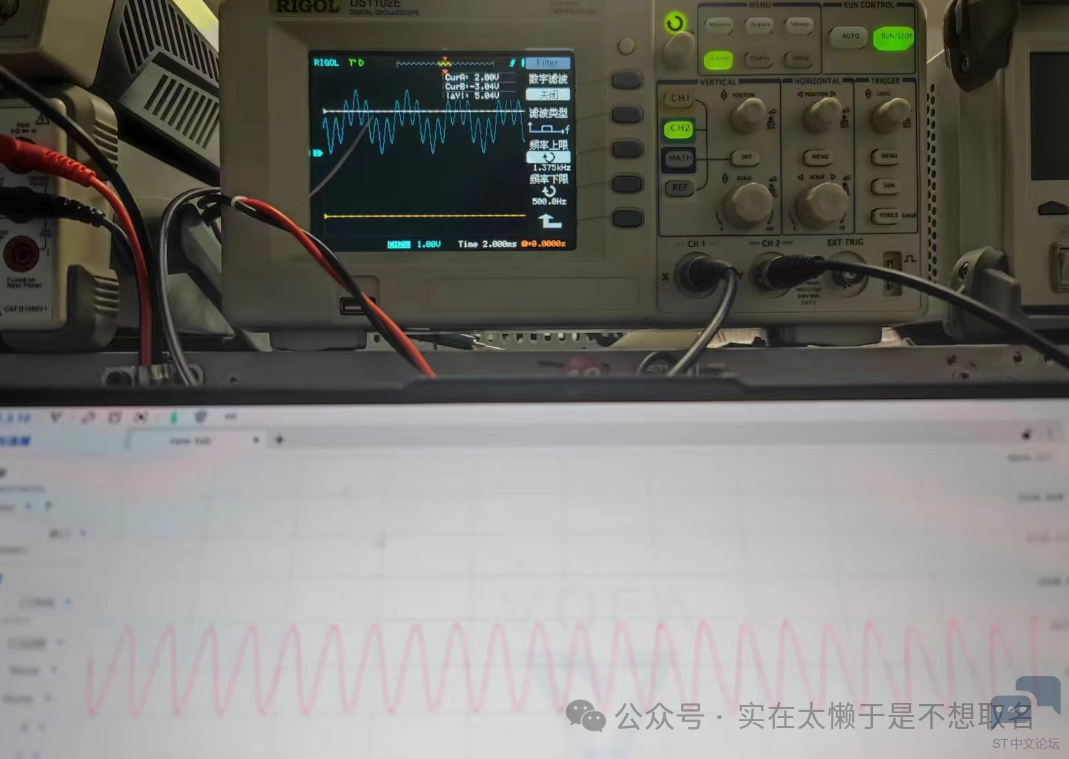



可以看到，我们非常轻松的从500HZ的信号中提取到了100HZ的信号。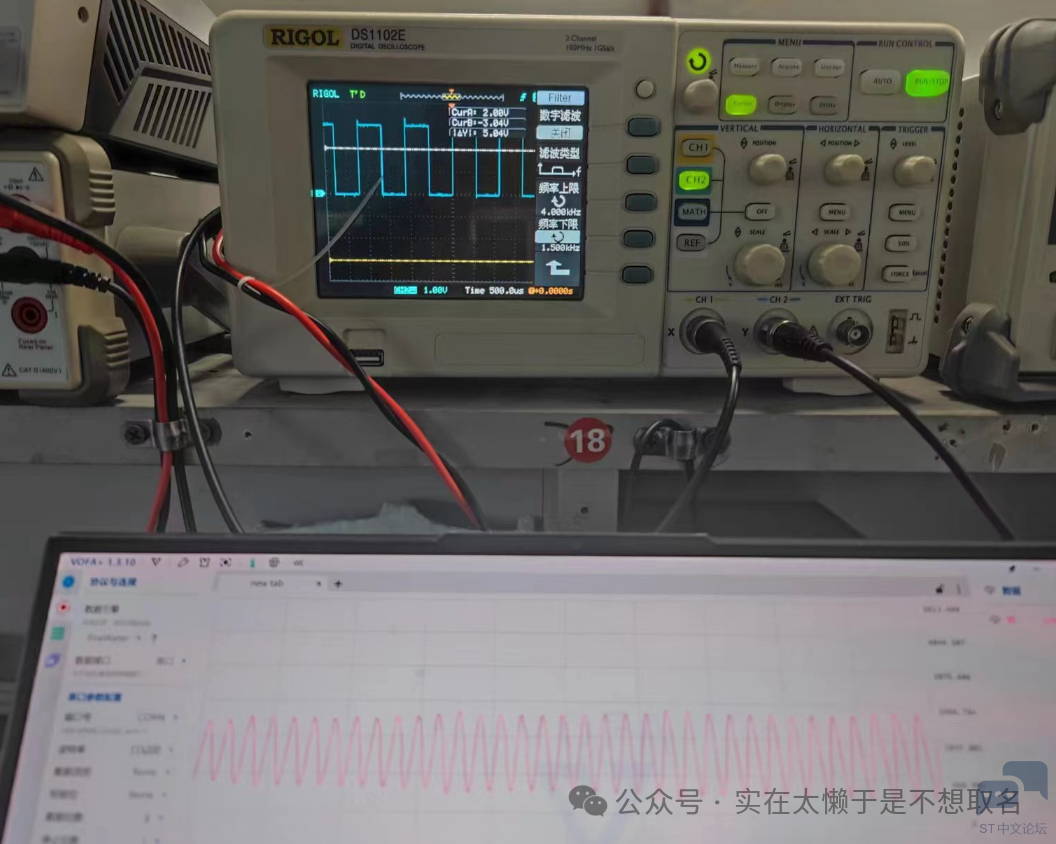



方波中提取其基波频率。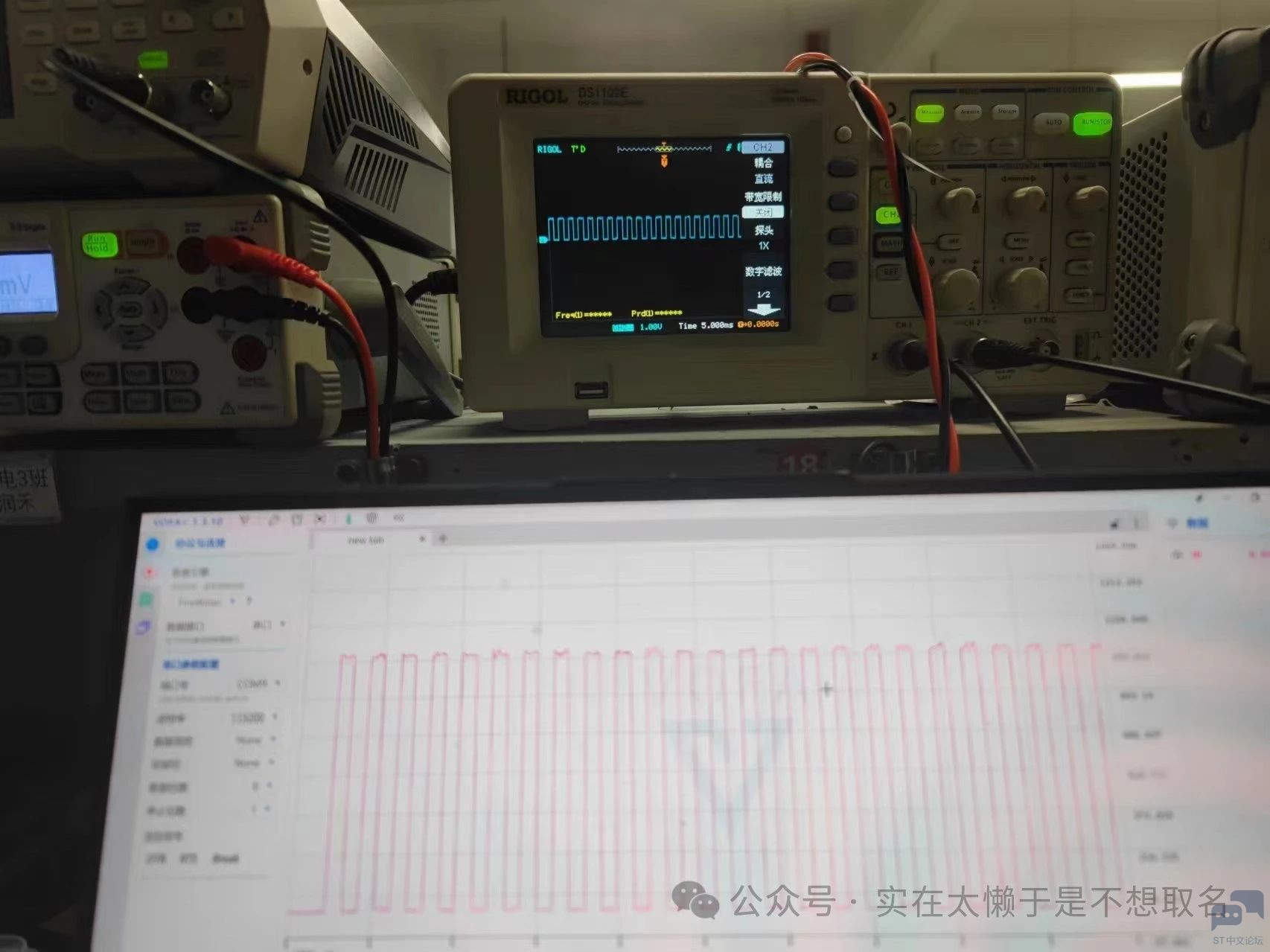



以及还有方波信号的 还原。

并且这个方法 的滤波精度相当之高。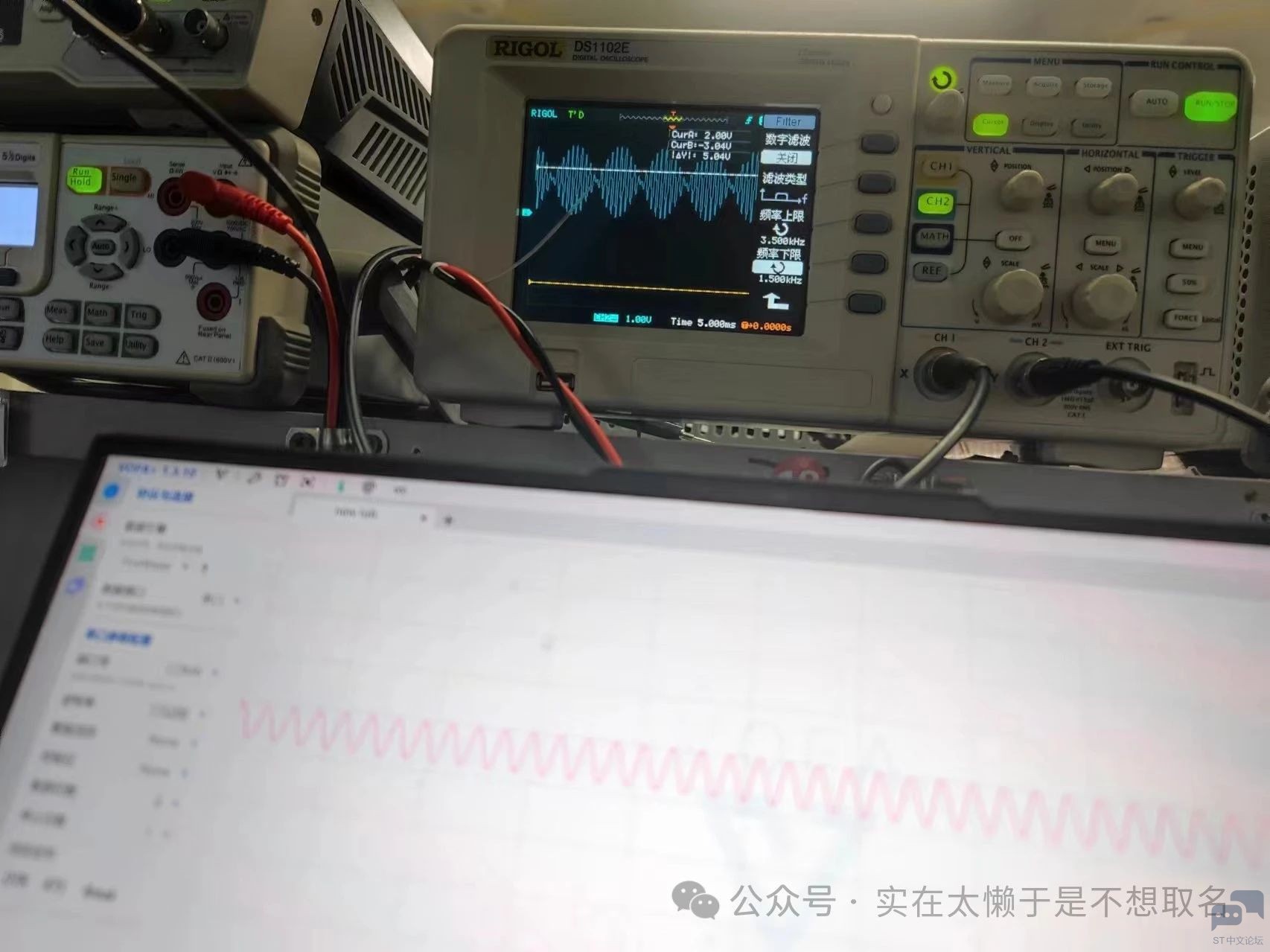



从一个900HZ叠加1000HZ的信号中将1000HZ的分量去掉。


转载自：电路小白
如有侵权请联系删除