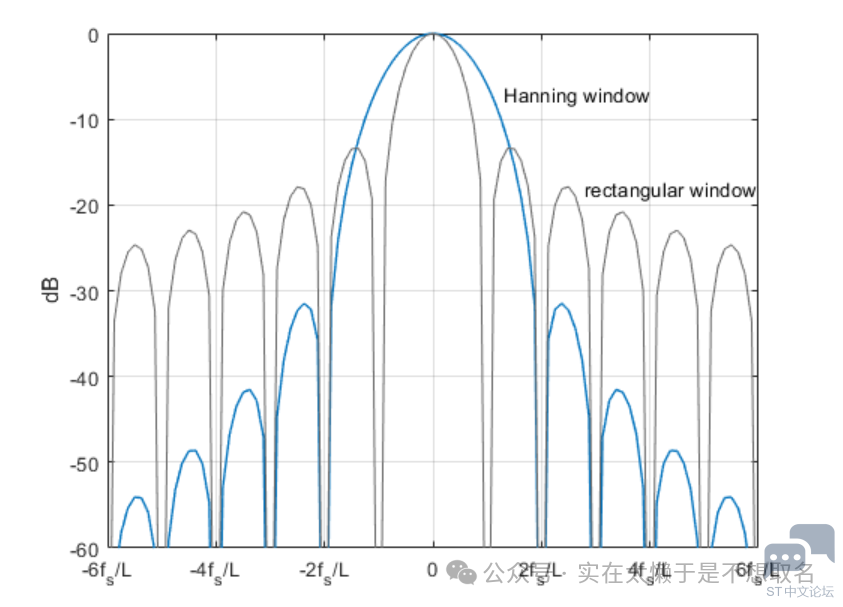
快速傅里叶变换(FFT)是一种数字信号处理中常用的技术,用于将快速序列转换为频域表示。在嵌入式系统中,如基于STM32的微控制器,实现FFT可以帮助解决信号处理的需求,例如声音处理、图像处理等。本文将介绍基于STM32的离散傅里叶变换的原理、实现方法和应用。
4 Z- Y1 S: A9 z* } h4 \8 M' G# l5 G- _- n$ E4 j4 p: D8 m) I8 U5 n# l
 4 P4 S+ |6 g5 c# r
4 P4 S+ |6 g5 c# r
8 R6 Z+ T' g! `6 _2 I
FFT是一种将时域序列转换为频域表示的技术,它将一个序列的N个采样点映射到频域中N个频率分量。其数学表达式如下:; F3 K" _$ \7 ]& ?0 |( C
8 K& g. L% O% p! ? D( c% Y0 Q
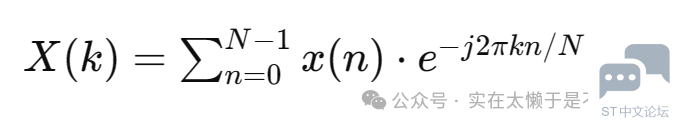
- G6 r; W' L" Q; g
; C- l ~$ |* T* ?- l: c其中,x(n) 是输入序列,X(k) 是输出的频域表示。# T7 \ ]3 Y$ R1 h5 R! f: j& l8 k2 f
9 _/ T- }' ~: I0 g3 l
准备工作:# j0 w1 \$ s1 s( K0 Q! ^
1 I5 O U! U" f" s* V1 a( m, k+ ^# U; T6 O( q# [# F* [! P# f
 6 x- ?8 M* M/ [9 g
6 x- ?8 M* M/ [9 g
2 e" ?& q$ d, e x+ `- S% \
G/ D2 U- ~3 S$ a3 @
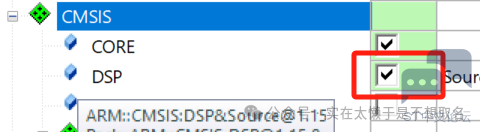
* f6 ?* j- P) `. ?/ ZKeil中的DSP库(Digital Signal Processing Library,数字信号处理库)是针对ARM Cortex-M处理器系列的一组软件库,用于提供各种数字信号处理功能的支持。这些库提供了一系列优化过的算法,可以帮助开发人员在嵌入式系统中高效地实现音频处理、图像处理、通信系统等各种信号处理应用。
2 p$ B0 @2 i( W
* v$ `4 ^/ W! ~5 Z因此我们需要在Keil中安装我们的DSP库。
3 K" \0 u/ O7 {4 t( d+ n# q7 I- #include "arm_math.h" // 包含DSP库
首先包含我们的DSP库。
& F( {! s" N" e5 B) I9 r% v
7 {# i I8 o& f7 S
" }8 j3 {& J! \( ~3 G. p$ B- #define FFT_LENGTH 100
9 R5 p" |8 S5 \6 M, v - // 输入序列! A3 `) J8 ~2 q* B# D
- float32_t inputSignal[FFT_LENGTH*2];
; ?& a/ e% S7 M$ x' m - 5 S+ N5 U h3 F$ _: _! \0 k& U
- // 输出序列,存储变换后的结果$ R2 g% P4 C& I) E
- float32_t outputSignal[FFT_LENGTH];
定义FFT的的输入和输出数组还有数组长度 m2 _2 Z4 O6 R4 W5 @; F0 j4 N; q
- arm_status status;; ^# E+ O5 u, v2 p* |
- arm_cfft_radix4_instance_f32 fft_inst;' T5 x4 F* ]6 b# s
- status = arm_cfft_radix4_init_f32(&fft_inst, FFT_LENGTH,0,1);
- void arm_cfft_radix4_init_f32(. a) }5 N) }3 j* S( t
- arm_cfft_radix4_instance_f32 * S,
; f3 j; n" c' U2 N7 m5 i - uint16_t fftLen,) _& B# G$ B5 t4 Q5 I
- uint8_t ifftFlag,5 C! f. Q+ }( m% T; n H' k
- uint8_t bitReverseFlag
6 |- r- w$ ^. I5 l8 z6 b6 N - );
定义一个状态变量用来显示FFT的初始化是否成功。
2 V* F0 [ f- { v; H- W7 i定义一个FFT的配置变量。: S1 Q) C5 z- `( C* N2 A, @ K
初始化FFT。3 t, J& d8 T, c, Z
S:指向 arm_cfft_radix4_instance_f32 结构体的指针,该结构体定义了 FFT 实例的状态信息。' C# m9 o+ I, x# r# ^+ v+ ?6 o
9 i4 d1 O& T& b. r* \- I
fftLen:FFT 的长度。' e5 U x% c4 u% ^: L
, q1 L6 s! f' R. o. F; L1 l
ifftFlag:指定是否进行逆变换。如果为 1,则表示初始化的是逆变换的 FFT;如果为 0,则表示初始化的是正变换的 FFT。6 r1 |. a8 O+ G) [9 ~% J
5 H7 E8 e* z8 ~( {& y# r8 w7 rbitReverseFlag:指定是否进行比特翻转。如果为 1,则表示进行比特翻转;如果为 0,则表示不进行比特翻转。
7 m) w' J' q; t% l* V
6 t; T6 p6 d1 e3 _& k) Z3 M" c在FFT算法中,比特(bit)反转是一种关键的步骤,用于将输入数据重新排列为正确的顺序,以便在后续的计算中进行有效处理。- }7 D7 K, E# R% |: E! x
- ~9 ]7 n" n' N4 b/ J& ~0 S* k当进行快速傅立叶变换时,算法要求输入数据的顺序是按照特定的方式排列的。特别是在使用基于分治法的算法(如Cooley-Tukey算法)时,输入数据的顺序必须满足按照一定规律的排列。7 _5 x! y3 U2 W+ `* l
+ G# z( K1 p! H1 [
在实际的FFT实现中,最常见的方式是通过比特反转来重新排列输入数据。比特反转就是将输入数据的比特位(二进制位)的顺序进行颠倒。这是因为在FFT算法中,数据会被分组,并按照一定规则进行反转,以便在每个阶段的运算中,数据可以正确地与其它组合进行配对。
/ \) l5 p- i% C. j6 _ H. }* n) q
* x v, e' {& K6 z; ~3 ?举个简单的例子,假设有一个长度为8的数据序列,按照0到7的顺序排列:% `1 M" f- Z' b$ X7 q# p& N1 D
. P5 Q0 S, c9 g4 M0 1 2 3 4 5 6 7! y+ J! ~" M J8 ~; [1 J
' O1 L+ G: k& c4 L% S( R3 N
在进行FFT时,需要按照一定规则重新排列这些数据。比特反转操作将会对这个数据序列进行如下的重新排列:
5 v1 {; |: {- F0 o; {9 _# N0 v$ r. z
0 4 2 6 1 5 3 7
: X' v4 i1 `) j6 J
. h- p# \1 l* X: O在FFT算法的每个阶段中,这种重新排列都会使得数据正确地与其它组合进行配对,从而实现快速傅立叶变换的计算。
3 g# ^ Y3 o& }$ {4 H
. X6 m) i% _9 M3 t: d0 a! P进行FFT并转换为模值
2 J5 L9 ~, `0 \% O* d- arm_cfft_radix4_f32(&fft_inst,inputSignal); //FFT计算
6 Y+ w7 a4 r, w8 o" f/ ^ - arm_cmplx_mag_f32(inputSignal,outputSignal,FFT_LENGTH); //取模得幅值
/ I0 I3 k7 k/ l% B; d. O6 l( K+ \对输入数组进行FFT变换,并将FFT的结果转化为模值。3 I7 W# u0 ~ H2 p
& N, g5 C; i# p# t& ~& F
测试+ j5 @$ L* h8 p- r! o0 n4 b. T
我们进行一个简单的测试# A, _: T* u A( r( g) T
- #define FFT_SIZE 1024& \& x* _/ [" z7 S' S& ]( B
- #define SAMPLE_RATE 1000+ ~6 D+ {7 A* u# f; E8 S5 E
- #define NUM_SAMPLES 1000
# b. U8 V+ V! X- i! w0 m* K - #define FREQ_OF_INTEREST 100
+ L" l# Y+ X+ o - for (int i = 0; i < NUM_SAMPLES; i++) {1 I' Y, g" c; f) e2 q1 \% s
- float32_t t = (float32_t)i / SAMPLE_RATE;
9 k/ w6 m Z7 V& v# a - float32_t sin_value = sinf(2 * PI * FREQ_OF_INTEREST * t); // 计算正弦波值
& U7 I. ]0 F" n1 }) y: Y2 H7 m7 W/ V - inputSignal[i * 2] = sin_value; // 实部
# m( H- n6 a4 k4 `5 h - inputSignal[i * 2 + 1] = 0; // 虚部% H; q. C% v! | w- p4 d
- }
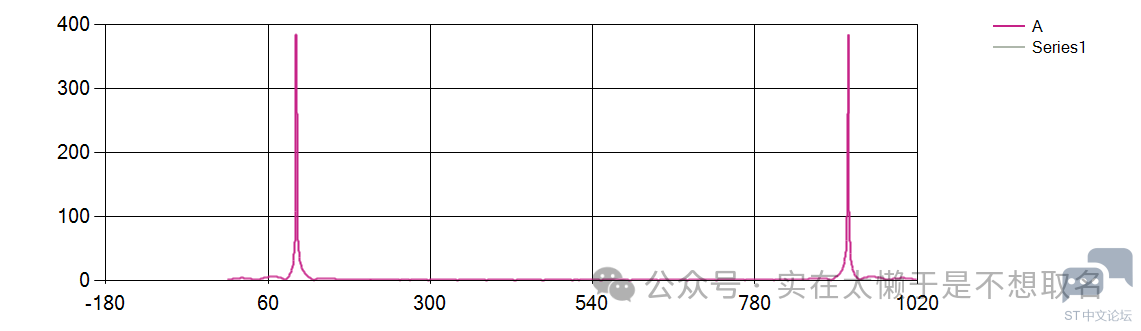
一千个点的采样值,频率假设为100HZ作为输入信号。* v2 |% t0 ?0 c k- T e: L
- for (int i = 0; i < FFT_SIZE; i++) {9 {" n7 G4 v3 X: ~" @, {
- // 计算复数的模值! V6 @+ l4 j6 n+ `# X7 B
- float32_t real = inputSignal[2 * i];( n- t6 i. m7 }4 v" h& B- B
- float32_t imag = inputSignal[2 * i + 1];
7 z: U9 o1 f0 A5 H/ w. P, m9 g# ` - float32_t magnitude = sqrtf(real * real + imag * imag);
% f" k/ H1 G- i* Z5 H/ H# z -
4 x% ]0 m5 u. V7 c7 f - // 打印每个频率分量的模值
! y, |5 y7 b: X& `7 n3 t' z+ t - printf("Magnitude: %f\n", magnitude);
6 D3 b7 M `' O - }
进行傅里叶变换后打印模值。+ j7 l& \2 o* K, a9 B" g! S
! {% K$ X6 I" X6 d: W. x2 k! x
" N. _# Q, `$ A h7 ?
/ d9 E4 X5 O; W9 Y, M2 h$ g可以看到傅里叶变换执行成功。; a/ O/ Q+ B) T8 S, a: f5 w
- for (int i = 0; i < NUM_SAMPLES; i++) {
3 o& \6 H( |; h6 t& Q: y* P - float32_t t = (float32_t)i / SAMPLE_RATE;
- z+ t7 `$ f5 L/ } - float32_t sin_value = sinf(2 * PI * FREQ_OF_INTEREST * t)+sinf(2 * PI * FREQ_OF_INTEREST * t*2)+sinf(3*2 * PI * FREQ_OF_INTEREST * t); // 计算正弦波值6 y3 p5 N; ?8 v' @
- inputSignal[i * 2] = sin_value; // 实部4 }$ L3 t) i3 M' ?+ \4 \% ~ j
- inputSignal[i * 2 + 1] = 0; // 虚部
/ n7 r# [' A5 G& |0 F! x5 R$ _% R: P - }
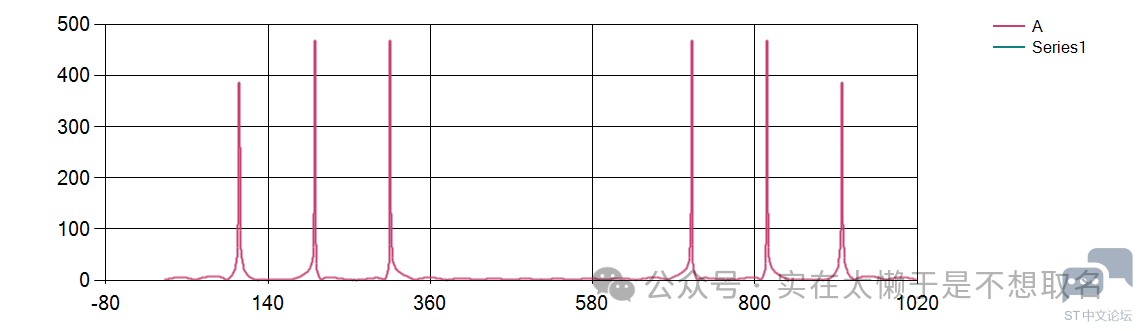
我们将信号制作成100HZ+200HZ+300HZ的信号。
5 w0 f/ ]! Z: d3 p1 P" L( @* z* J4 c$ o5 q; j+ n _: Z# t; T
 $ \1 e! B K3 H3 n+ F7 X
$ \1 e! B K3 H3 n+ F7 X
9 `3 J N/ s g# X! ^) p
8 J, k3 D% J+ \
' k# I, j/ L" V/ w/ n) w转载自:电路小白
) B' h0 }9 o% H" H6 F n a如有侵权请联系删除
. p( H# F2 h( {7 n9 I& Q* A' l2 e3 f* y- z
|


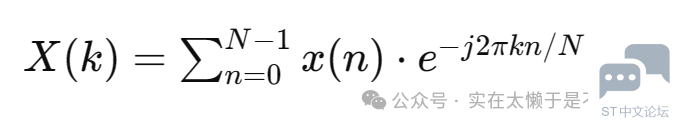




 微信公众号
微信公众号
 手机版
手机版

这个FFT不错,学习参考一下