快速傅里叶变换（FFT）是一种数字信号处理中常用的技术，用于将快速序列转换为频域表示。在嵌入式系统中，如基于STM32的微控制器，实现FFT可以帮助解决信号处理的需求，例如声音处理、图像处理等。本文将介绍基于STM32的离散傅里叶变换的原理、实现方法和应用。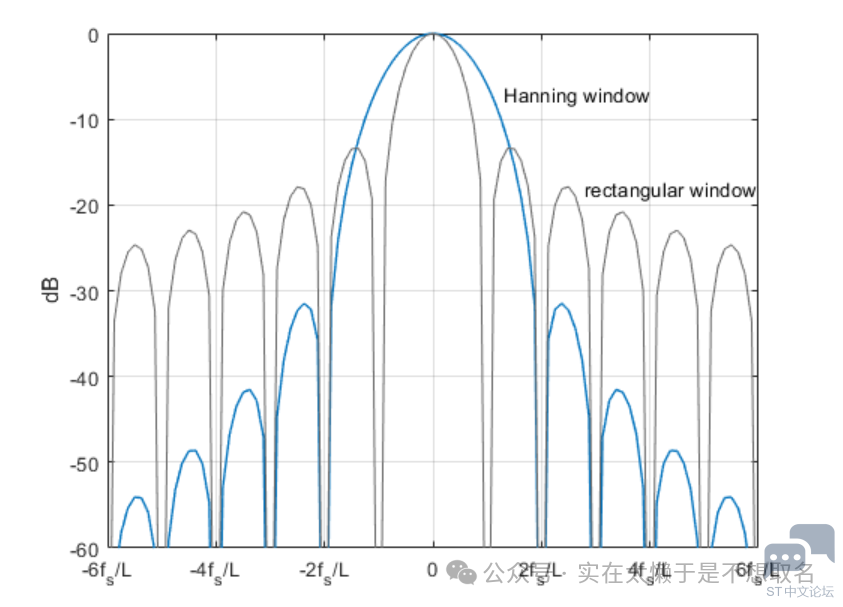



FFT是一种将时域序列转换为频域表示的技术，它将一个序列的N个采样点映射到频域中N个频率分量。其数学表达式如下：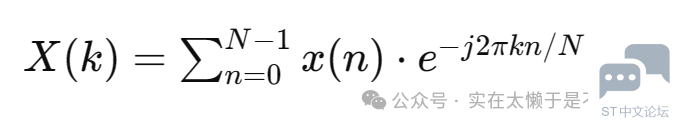



其中，x(n) 是输入序列，X(k) 是输出的频域表示。

准备工作：






Keil中的DSP库（Digital Signal Processing Library，数字信号处理库）是针对ARM Cortex-M处理器系列的一组软件库，用于提供各种数字信号处理功能的支持。这些库提供了一系列优化过的算法，可以帮助开发人员在嵌入式系统中高效地实现音频处理、图像处理、通信系统等各种信号处理应用。

因此我们需要在Keil中安装我们的DSP库。

1. #include "arm_math.h" // 包含DSP库

复制代码

首先包含我们的DSP库。

1. #define FFT_LENGTH 100
   
2. // 输入序列
   
3. float32_t inputSignal[FFT_LENGTH*2];
   
4. 
   
5. // 输出序列，存储变换后的结果
   
6. float32_t outputSignal[FFT_LENGTH];

复制代码

定义FFT的的输入和输出数组还有数组长度

1. arm_status status;
   
2.     arm_cfft_radix4_instance_f32 fft_inst;
   
3.     status = arm_cfft_radix4_init_f32(&fft_inst, FFT_LENGTH,0,1);

复制代码

1. void arm_cfft_radix4_init_f32(
   
2.   arm_cfft_radix4_instance_f32 * S,
   
3.   uint16_t fftLen,
   
4.   uint8_t ifftFlag,
   
5.   uint8_t bitReverseFlag
   
6. );

复制代码

定义一个状态变量用来显示FFT的初始化是否成功。
定义一个FFT的配置变量。
初始化FFT。
S：指向 arm_cfft_radix4_instance_f32 结构体的指针，该结构体定义了 FFT 实例的状态信息。

fftLen：FFT 的长度。

ifftFlag：指定是否进行逆变换。如果为 1，则表示初始化的是逆变换的 FFT；如果为 0，则表示初始化的是正变换的 FFT。

bitReverseFlag：指定是否进行比特翻转。如果为 1，则表示进行比特翻转；如果为 0，则表示不进行比特翻转。

在FFT算法中，比特（bit）反转是一种关键的步骤，用于将输入数据重新排列为正确的顺序，以便在后续的计算中进行有效处理。

当进行快速傅立叶变换时，算法要求输入数据的顺序是按照特定的方式排列的。特别是在使用基于分治法的算法（如Cooley-Tukey算法）时，输入数据的顺序必须满足按照一定规律的排列。

在实际的FFT实现中，最常见的方式是通过比特反转来重新排列输入数据。比特反转就是将输入数据的比特位（二进制位）的顺序进行颠倒。这是因为在FFT算法中，数据会被分组，并按照一定规则进行反转，以便在每个阶段的运算中，数据可以正确地与其它组合进行配对。

举个简单的例子，假设有一个长度为8的数据序列，按照0到7的顺序排列：

0 1 2 3 4 5 6 7

在进行FFT时，需要按照一定规则重新排列这些数据。比特反转操作将会对这个数据序列进行如下的重新排列：

0 4 2 6 1 5 3 7

在FFT算法的每个阶段中，这种重新排列都会使得数据正确地与其它组合进行配对，从而实现快速傅立叶变换的计算。

进行FFT并转换为模值

1. arm_cfft_radix4_f32(&fft_inst,inputSignal);          //FFT计算
   
2.     arm_cmplx_mag_f32(inputSignal,outputSignal,FFT_LENGTH);  //取模得幅值

复制代码

对输入数组进行FFT变换，并将FFT的结果转化为模值。

测试
我们进行一个简单的测试

1. #define FFT_SIZE 1024
   
2. #define SAMPLE_RATE 1000
   
3. #define NUM_SAMPLES 1000
   
4. #define FREQ_OF_INTEREST 100
   
5. for (int i = 0; i < NUM_SAMPLES; i++) {
   
6.         float32_t t = (float32_t)i / SAMPLE_RATE;
   
7.         float32_t sin_value = sinf(2 * PI * FREQ_OF_INTEREST * t); // 计算正弦波值
   
8.         inputSignal[i * 2] = sin_value; // 实部
   
9.         inputSignal[i * 2 + 1] = 0; // 虚部
   
10.     }

复制代码

一千个点的采样值，频率假设为100HZ作为输入信号。

1. for (int i = 0; i < FFT_SIZE; i++) {
   
2.         // 计算复数的模值
   
3.         float32_t real = inputSignal[2 * i];
   
4.         float32_t imag = inputSignal[2 * i + 1];
   
5.         float32_t magnitude = sqrtf(real * real + imag * imag);
   
6.         
   
7.         // 打印每个频率分量的模值
   
8.         printf("Magnitude: %f\n", magnitude);
   
9.     }

复制代码

进行傅里叶变换后打印模值。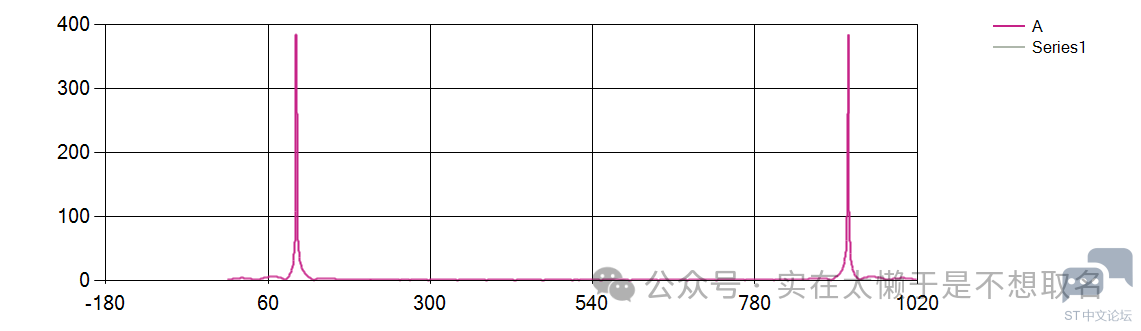



可以看到傅里叶变换执行成功。

1. for (int i = 0; i < NUM_SAMPLES; i++) {
   
2.         float32_t t = (float32_t)i / SAMPLE_RATE;
   
3.         float32_t sin_value = sinf(2 * PI * FREQ_OF_INTEREST * t)+sinf(2 * PI * FREQ_OF_INTEREST * t*2)+sinf(3*2 * PI * FREQ_OF_INTEREST * t); // 计算正弦波值
   
4.         inputSignal[i * 2] = sin_value; // 实部
   
5.         inputSignal[i * 2 + 1] = 0; // 虚部
   
6.     }

复制代码

我们将信号制作成100HZ+200HZ+300HZ的信号。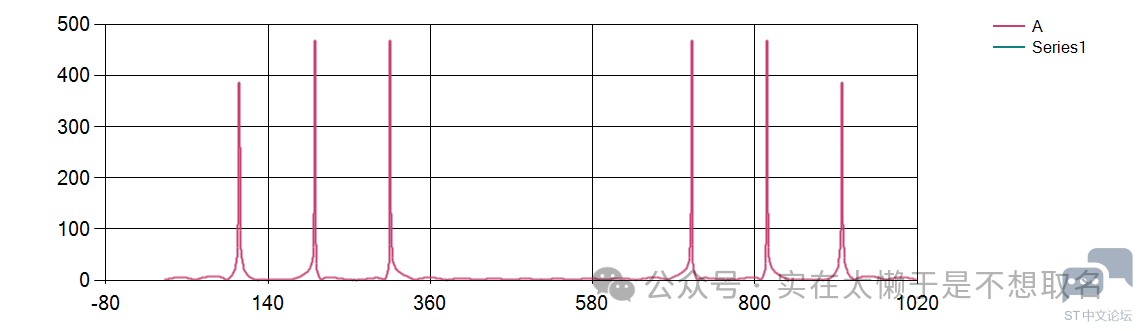





转载自：电路小白
如有侵权请联系删除

这个FFT不错，学习参考一下