基于STM32直流电机中PID的控制

[复制链接]

攻城狮Melo 发布时间：2023-3-18 11:59

文章
文章封面:
文章简介:	基于STM32直流电机中PID的控制

一.PID控制算法
1.什么是PID
PID：Proportion-Integral-Differential

在过程控制中，我们经常使用的一种算法就是PID算法了，所谓PID控制算法就是对偏差进行比例、积分、微分控制，来使偏差趋于某一固定的值，PID核心由三个单元组成：比例单元（P）、积分单元（I）、微分单元（D），PID实际上就是误差控制。

PID控制系统（模拟）的框图如下：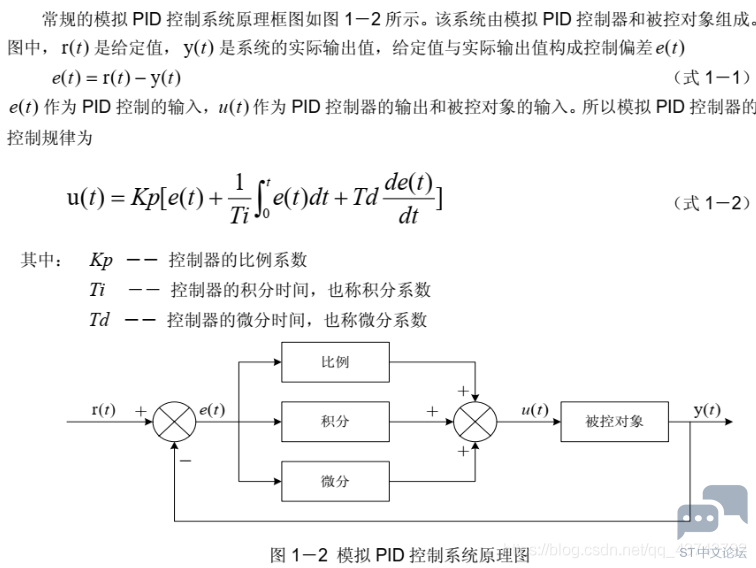

2.PID系数的理解
理解PID的三个系数，可以结合PID调节时候的响应曲线，要使实际中的响应曲线趋近于理想状态下的响应曲线，无非就是三点灵魂：快速（P）、准确（I）、稳定（D），要想控制的变量保持在完美的状态，这三个灵魂就必须调整好。

以下分析中的：P、I、D都指的是PID的三个系数

下面从三个系数对整体控制的影响做出分析

Ⅰ.比例（P）部分
输入值一旦与目标值产生偏差e，就需要缩小偏差，P就是用来缩小偏差的，使控制量向减少偏差的方向改变，而且P越大，偏差缩小的速度就越快，所以P的作用就是使控制量更快地接近目标值。

但是！十肇九快！！！P过大的时候，就容易刹不住，很容易超出目标值，当超出目标值时，又会反向朝目标值飞奔，然后又太快了，再次偏离目标值，然后又朝目标值…这样反反复复的在目标值附近震荡，这就是P太大的弊端：不够稳定。

所以，P大了虽然可以快速响应，但也容易产生震荡，破坏系统的稳定性，可以适当增大D来提高稳定性。

Ⅱ.积分（I）部分
积分的表达式如下：

从其表达式中可以看出，只要存在偏差，积分结果就会不断增加，也就是控制作用会不断增加；当偏差为0时，积分结果是一个常数，此时控制作用才可能是一个稳定的值。

所以直观的来看，积分可以消除系统的静态偏差，因为一旦有误差，积分就会增加，系统就会做出反应，直到偏差为0，也就是积分保证了控制的准确性。

积分的作用虽然会消除静态偏差，但是也会拉低系统的响应速度，就是说I对P有抑制作用。

Ⅲ.微分（D）部分
上面说了，P过大会引起震荡，降低系统稳定性，可以通过提高D来减小震荡。

微分的作用就是根据偏差的变化趋势预先给出纠正！怎么个预先法呢？因为微分可以看作是求导，上过高中同鞋都知道：求导可以反映函数的变化趋势。所以，通过微分，可以对偏差的变化进行预判地抑制，防止矫枉过。

微分的引入，有助于减小震荡，使系统趋于稳定，D越大，抑制P的效果就越强。

3.PID的数字化处理
由于计算机控制是一种采样控制，只能根据采样时刻的偏差值计算控制量，所以我们是通过软件实现控制算法的，要对PID进行离散化处理（也就是数字化处理），就是根据离散采样点的偏差值进行控制，在离散化处理后，相比于模拟控制由如下改变：
由差分代替微分
由累加代替积分
数字化处理后的PID系统如下：

采样的周期越小，就越接近模拟控制，控制的效果也就越好。

二.位置闭环控制
位置闭环控制，也叫位置式PID控制，就是传统的PID控制，控制的偏差逐渐接近0，从而使控制量趋于目标值。

对电机使用位置闭环控制的时候，就是控制电机的转动位置，通过编码器的脉冲累加测量电机的位置信息，与目标位置进行比较，得到偏差值，通过比例、积分、微分的PID算法进行控制，使偏差趋于0。

电机控制中，输出量就是电机控制模块输出的占空比，作用于电机转速，此时离散PID的公式如下：

其控制框图如下：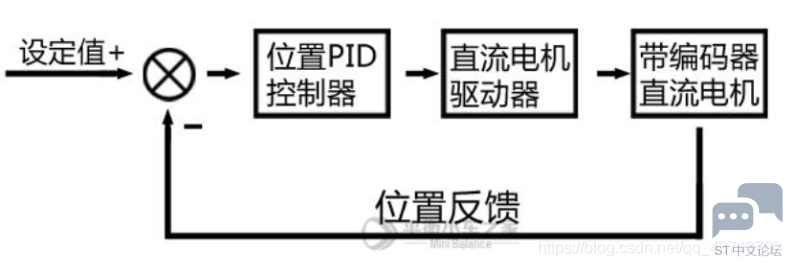

控制实现代码如下：

/* 返回输出
* Encoder为输入（编码器测量的信号，也就是电机转速）
* Target为目标值
*/
//KP、KI、KD为PID的系数
int Postition_PID( int Encoder, int Target )
{ //依次的变量代表：偏差、输出、偏差积分、偏差微分
static float Bias,Pwm,Integral_bias,Last_bias;
Bias = Encoder-Target;//计算偏差
Integral_bias += Bias;//计算偏差积分，累加
Pwm = KP*Bias+KI*Integral_bias+KD*(Bias-Last_bias);//计算输出，根据PID
Last_bias = Bias;//保存为上一次偏差
return Pwm;//返回输出
}

复制代码

在定时中断里实现PID控制，定时中断相当于离散的采样点，中断服务函数中可调用控制函数：

//中断中如下调用
Moto = Postition_PID( Encoder, Target );
//最终的控制落回到控制电机转速上
Set_Pwm( Moto );

复制代码

最终的控制要落回到电机的控制上，也就是电机的转速控制——PWM控制。

位置控制的调节经验：先只使用P控制，逐渐增大P，系统震荡后加入微分控制D来抑制震荡，调整KD直至消除震荡，之后再根据系统对响应和静差的要求，调节P、I参数。

三.速度闭环控制
速度闭环控制也可叫增量式PID控制，与位置式PID控制不同，位置式PID输出的是控制量新的状态，而增量式PID输出的是控制量的增值，增量式PID的离散公式如下：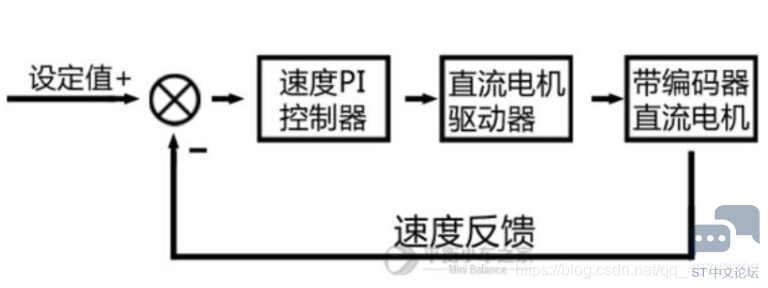

位置闭环控制是使电机准确转到某一位置，速度闭环控制是使电机以某一速度转动，在速度闭环控制里，我们只需要使用PI控制即可，所以简化后的公式如下：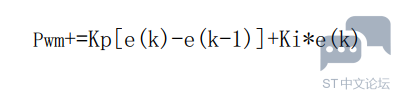

注意：公式直接将控制量的增量加在上一次控制量的状态上了！！！

控制框图如下：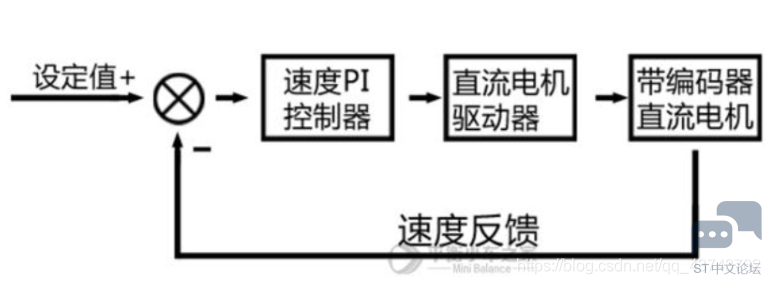

控制代码如下：

/* 返回输出
* Encoder为输入（编码器测量的信号，也就是电机转速）
* Target为目标值
*/
//KP、KI为PID的系数
int Incremental_PI( int Encoder, int Target )
{ //依次的变量代表：偏差、输出、偏差微分
static float Bias,Pwm,Last_bias;
Bias = Encoder-Target;//计算偏差
Pwm += KP*(Bias-Last_bias)+KI*Bias;//增量式PI
Last_bias = Bias;//保存为上一次偏差
return Pwm;//返回输出
}

复制代码

在定时中断里实现PID控制，定时中断相当于离散的采样点，中断服务函数中可调用控制函数：

//中断中如下调用
Moto = Incremental_PI( Encoder, Target );
//最终的控制落回到控制电机转速上
Set_Pwm( Moto );

复制代码

要注意速度闭环控制采用PI控制，公式与PID有所不同，输出的也是控制量的增量，这里将增量直接加在了上一次的状态量上，所以输出的还是控制量的新状态。

最后附上我找到的PID参数调整口诀：

常用口诀：
参数整定找最佳，从小到大顺序查
先是比例后积分，最后再把微分加
曲线振荡很频繁，比例度盘要放大
曲线漂浮绕大湾，比例度盘往小扳
曲线偏离回复慢，积分时间往下降
曲线波动周期长，积分时间再加长
曲线振荡频率快，先把微分降下来
动差大来波动慢。微分时间应加长
理想曲线两个波，前高后低4比1
一看二调多分析，调节质量不会低
————————————————
版权声明：Aspirant-GQ
如有侵权请联系删除