本文开始前我们先简单的介绍一下什么是THD?

总谐波失真（Total Harmonic Distortion，简称THD）是衡量信号失真程度的重要指标，特别是在音频、电力电子设备和通信系统等领域。THD表示一个信号中谐波分量（除了基波之外的频率分量）相对于基波的比例。具体来说，THD是所有谐波分量的平方和与基波分量平方的比值的平方根，通常用百分比表示。

公式表示为：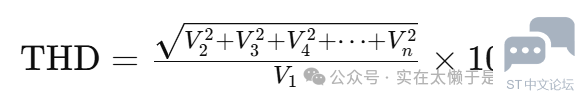


其中的V1是基波幅度，V2,V3……Vn是谐波幅度。

这个公式很好理解，一个信号的谐波幅度平方和占谐波频率的百分比。

那么如何获取基波幅度和谐波幅度，就是我们的FFT需要进行的事情。

利用FFT我们可以获取信号的频率谱。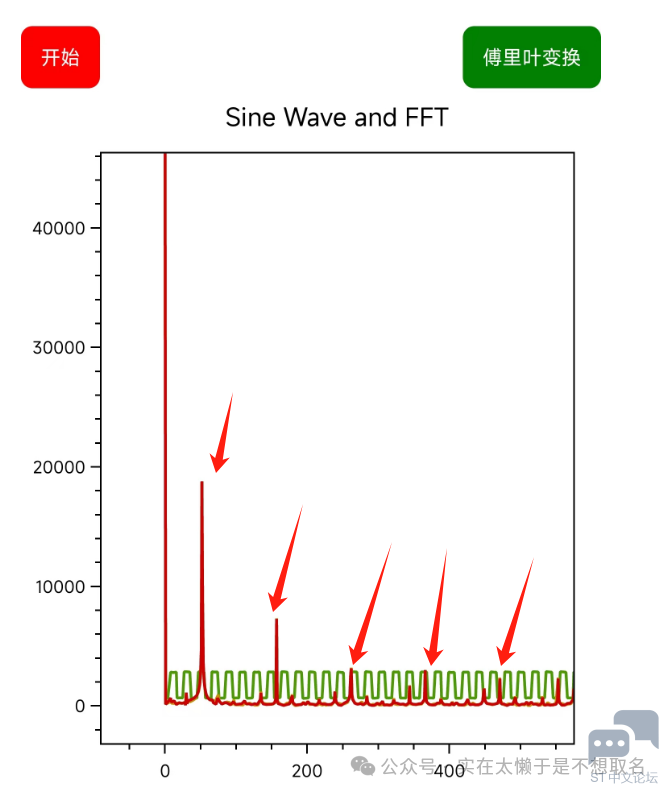



例如一段信号方波信号经过FFT之后，这些突出的方波信号就是谐波的幅值，而第一段（不包括第一个点）的则是其基波幅度。但是这里不包含第一个点，因为那个点是直流的幅度（两倍）。

因此我们只需要进行FFT之后统计谐波的平方和即可获得我们的THD。

快速傅里叶变换
关于FFT我们在之前的文章中有过介绍，我们在Keil中可以利用DSP库来进行快速的FFT（手搓的FFT算法效率通常很低）。我们在之前的文章中介绍过如何使用ADC+DMA的快速采样配合DSP库进行FFT。



STM32的DMA采样+FFT时域分析（STM32F407）

我们同样的在这篇文章的基础上进行。

1. #define ADCLenth 1024
   
2. uint16_t ADCValue[ADCLenth];
   
3. arm_cfft_radix4_instance_f32 scfft;//定义scfft结构体
   
4. float FFT_InputBuf[ADCLenth*2];  //FFT输入数组
   
5. float FFT_OutputBuf[ADCLenth];  //FFT输出数组

复制代码

我们定义一个FFT的结构体变量，以及存放ADC采样结果的数组还有FFT的输入输出数组，这里的输入数组之所以长度翻倍是因为对于FFT的输入来说是一个复数即包含实部和虚部，因此长度是两倍。

1.         for(int i=0; i < ADCLenth; i++)
   
2.         {
   
3.           FFT_InputBuf[2*i]=(ADCValue[i] )*3.3/4096; //实部
   
4.           FFT_InputBuf[2*i+1]=0;          //虚部
   
5.         }
   
6.         arm_cfft_radix4_f32(&scfft,FFT_InputBuf);  
   
7.         arm_cmplx_mag_f32(FFT_InputBuf,FFT_OutputBuf,ADCLenth);  //取模得幅值
   
8.         
   
9. 
   
10.         for(int i = 2;i<ADCLenth/2;i++)
    
11.         {
    
12.           if(FFT_OutputBuf[i]>maxValue)
    
13.           {
    
14.          
    
15.             maxValue = FFT_OutputBuf[i];
    
16.             max = i;
    
17.          
    
18.           }
    
19.         }

复制代码

一轮ADC采样结束之后，我们将其的实部信号和虚部信号（0）存放FFT的输入数组，之后执行快速傅里叶变换获得FFT的模值，模值存放在FFT_OutputBuf中。

我们通过一个比较循环来寻找FFT结果的最大值，这里我们忽略前几个元素尤其是索引为0的位置，因为他是直流分量的模值。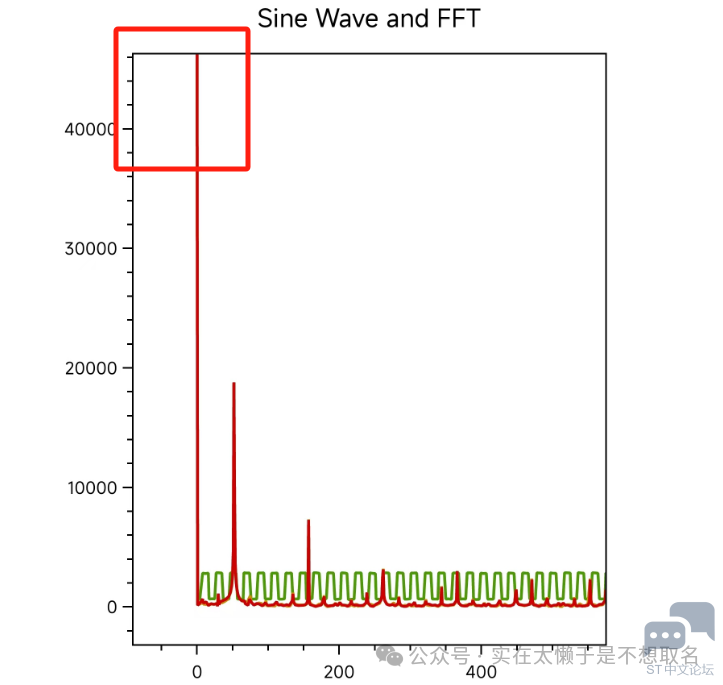



之后我们就需要统计各个谐波的幅度。

1. float FindMax(float * fft,int index,int wind)
   
2. {
   
3.   int max = 0;
   
4.   for(int i = index-wind ;i <index+wind;i++)
   
5.   {
   
6.     if(fft[i]>max)
   
7.     {
   
8.       max =fft[i];
   
9.     }
   
10.    
    
11.   }
    
12.   return max;
    
13.   
    
14. }

复制代码

我们定义一个函数来寻找某点附近的最大值，这里之所以要寻找某点附近的最大值在这里说明一下。

FFT的索引和频率有关系，每个索引对应的频率之差为：采样频率/采样长度。我们的采样长度是1024，而采样频率是20kHZ,因此索引差为对应的频率差为19.53HZ，因为根据计算，1000HZ的频率对应的索引为51.2而由于索引只能是整数，因此在频谱上基波的最大值并不会是51.2而是51，因为int类型会抛弃小数。

所以我们实际统计的是984.3HZ或者1015.56HZ的频率，这样子我们计算谐波幅度进行翻倍的时候并不会是刚刚好好的对应的2KHZ的频率，而是其最大幅度会发生便宜。

因此我们因为是寻找我们认为的谐波索引的附近最大值。

1.         for(int i = max;i<ADCLenth/2;i+=max)
   
2.         {
   
3.           maxW = FindMax(FFT_OutputBuf,i,max*0.3);
   
4.           all =all +  maxW*maxW;
   
5.         }
   
6.         all = all - maxValue*maxValue;
   
7.         
   
8.         DHT = sqrtf(all)/maxValue;
   
9.         printf("DHT:%f%c\r\n",DHT*100,'%');
   
10.         all = 0;
    
11.         max = 2;
    
12.         maxValue = 0;

复制代码

这样子就是统计我们的THD的值，之后将其打印，这里计算谐波幅度的时候我把基波的幅度也加了上去，我们将其去除。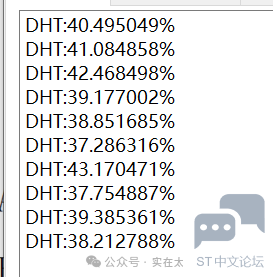



可以看到外面的THD（图中打错了）计算外面的方波频率的THD在40%左右。
我们利用MatLab生成一下方波信号之后用FFT来看一下理论结果。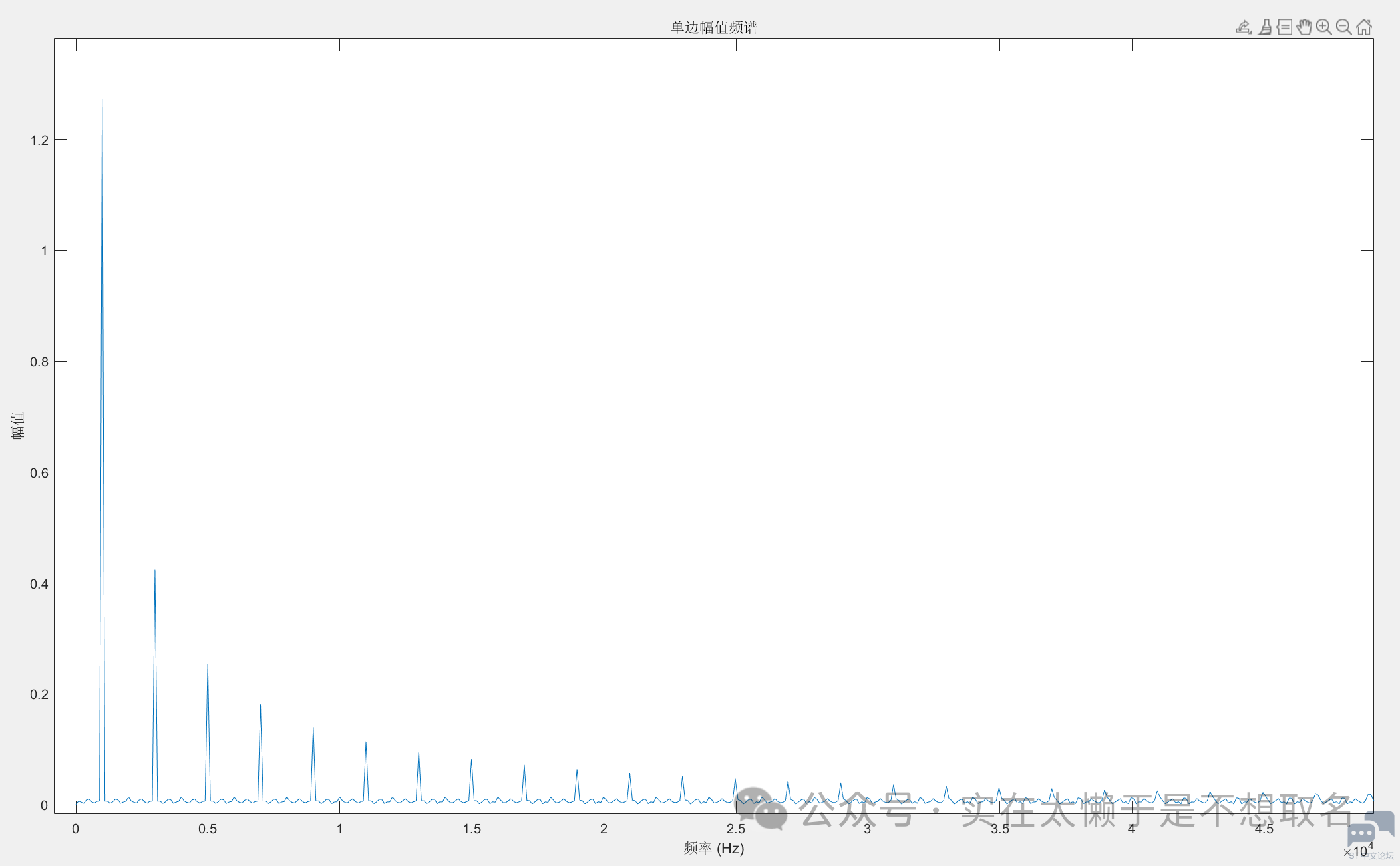





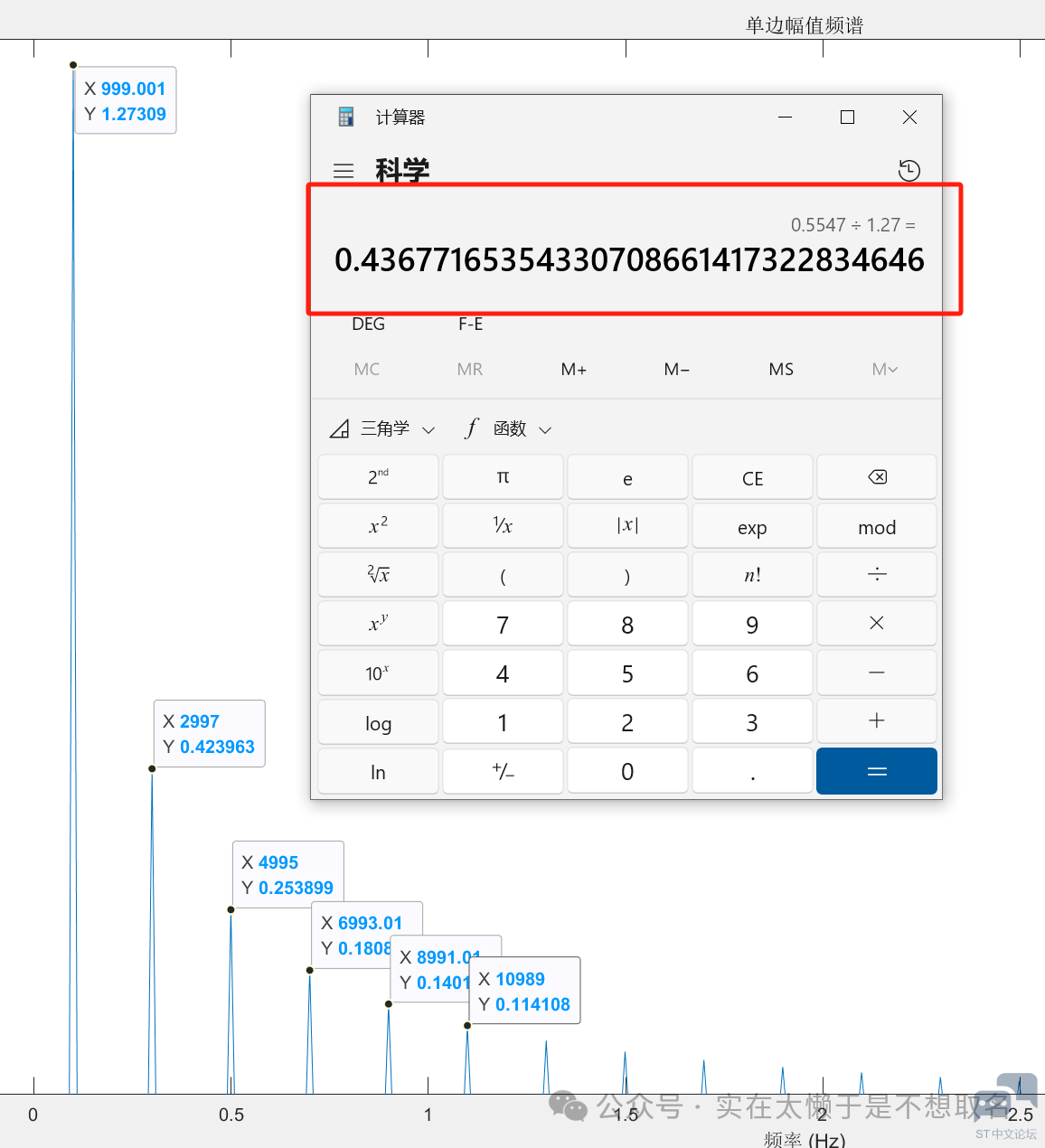
其统计到5次谐波对应的值计算出的THD的值43%，这和我们的计算结果也很接近了。
我们同样的看一下手机上的显示内容。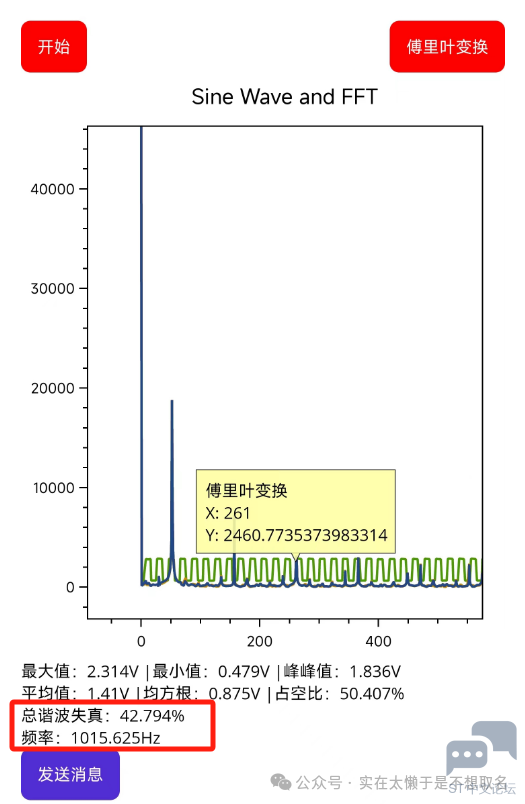



总谐波失真为42.7%


转载自：电路小白
如有侵权请联系删除