【经验分享】FFT变换结果的物理意义

[复制链接]

STMCU小助手发布时间：2021-12-25 22:00

文章
文章封面:
文章简介:	FFT变换结果的物理意义

26.1 初学者重要提示
下个章节为大家介绍两个重要知识点：频谱泄露和栅栏效应，推荐学习完毕本章后看一下。

26.2 FFT变换结果的物理意义
26.2.1 理论阐释
虽然很多人都知道FFT是什么，可以用来做什么，怎么去做，但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。

一个模拟信号，经过ADC采样之后，就变成了数字信号。采样定理告诉我们，采样频率要大于信号频率的两倍（要满足奈奎斯特采样定律）。

采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。

假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即0Hz），而最后一个点 N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被 N-1个点平均分成N等份，每个点的频率依次增加。例如某点n所表示的频率为：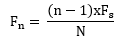

aHR0cHM6Ly9pbWcyMDIwLmNuYmxvZ3MuY29tL2Jsb2cvMTM3OTEwNy8yMDIwMDUvMTM3OTEwNy0yMDIw.png

由上面的公式可以看出，Fn所能分辨到频率为 Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是：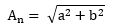

相位就是：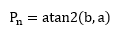

根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：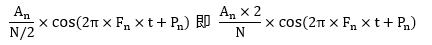

对于n=1点的信号，是直流分量，幅度即为A1/N。由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。
$ J* G' A9 {! Q/ j1 v1 X% D
26.2.2       理论计算和Matlab实际计算结果对比
下面以一个实际的信号来做说明：

假设我们有一个信号，它含有2V的直流分量，频率为50Hz、相位为-30度、幅度为3V的交流信号，以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下：

x = 2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)

式中cos参数为弧度，所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样，总共采样256点。按照我们上面的分析，Fn=(n-1)*Fs/N，我们可以知道，每两个点之间的间距就是1Hz，第n个点的频率就是n-1。我们的信号有3个频率：0Hz、50Hz、75Hz，应该分别在第1个点、第51个点、第76个点上出现峰值，其它各点应该接近0。实际情况如何如下：

第一步：在matlab上新建.m文件，文件内容如下：
Fs = 256;       % 采样率
N  = 256;       % 采样点数
n  = 0:N-1;       % 采样序列
t  = 0:1/Fs:1-1/Fs;  % 时间序列

x = 2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180) ;  %原始信号

y = fft(x); %对原始信号做FFT变换
M = abs(y);  %求FFT转换结果的模值
plot(n, M); %绘制FFT转换模值的曲线
第二步：运行后显示效果如下：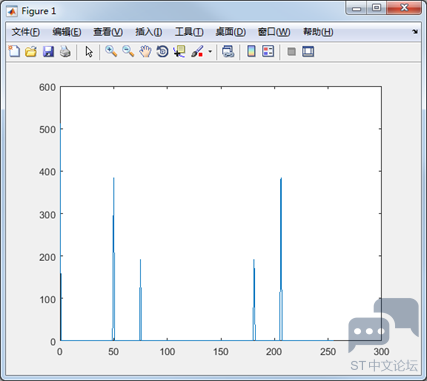

第三步：从matlab的工作区获得几个关键点及其附近两个点的幅值：

1点，2点，3点的数值如下：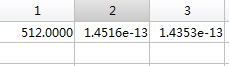

50点，51点，52点的数值如下：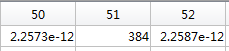

75点，76点，77点的数值如下：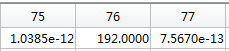

按照上面说的公式，可以计算出：

直流分量为： 512/N=512/256=2；

50Hz信号的幅度为：384/(N/2)=384/(256/2)=3；

75Hz信号的幅度为：192/(N/2)=192/(256/2)=1.5。可见，从频谱分析出来的幅度是正确的。

第四步：计算相位
计算相位要获取FFT变换后相应频率点幅值的实部和虚部，这里看第一步代码中的y变量数值即可。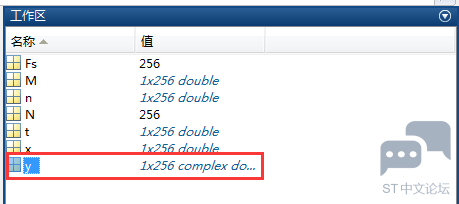

由于直流信号没有相位可言。这里主要看50Hz的相位和75Hz的相位。

1、计算50Hz信号的相位。

y变量的第51点对应数值：332.553755053225 - 192.000000000000i

那么atan2(-192, 332.553)=-0.5236，这个结果是弧度，换算成角度180*(-0.5236)/pi=-30.0001。

这个结果与cos(2*pi*50*t-pi*30/180)中相位是相符的。

2、计算75Hz信号的相位。

y变量的第76点对应数值：3.43858275186904e-12 + 192.000000000000i

那么atan2(192, 3.43858275186904e-12)=1.5708弧度，换算成角度180*1.5708/pi=90.0002。这个结果与cos(2*pi*75*t+pi*90/180)中的相位是相符的。

总结
根据FFT结果以及上面的分析计算，我们就可以写出信号的表达式了，它就是我们开始提供的信号。

总的来说，这个过程就是这样：假设采样频率为Fs，采样点数为N，做FFT之后，某一点n（n从1开始）表示的频率为：Fn=(n-1)*Fs/N；该点的模值除以N/2就是对应该频率下的信号的幅度（对于直流信号是除以N）；该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值，范围从-pi到pi。要精确到xHz，则需要采样长度为1/x秒的信号，并做FFT。要提高频率分辨率，就需要增加采样点数，这在一些实际的应用中是不现实的，需要在较短的时间内完成分析。解决这个问题的方法有频率细分法，比较简单的方法是采样比较短时间的信号，然后在后面补充一定数量的0，使其长度达到需要的点数，再做FFT，这在一定程度上能够提高频率分辨力。具体的频率细分法大家可参考相关文献。

26.3 FFT变换的频谱泄露问题
为了说明频谱泄露的问题，这里我们具一个求解方波FFT变换的例子。在matlab中运行如下代码：

Fs = 256;          % 采样率
N  = 256;          % 采样点数
n  = 0:N-1;       % 采样序列
t  = 0:1/Fs:1-1/Fs; % 时间序列
x = square(2*pi*30*t,  50);  %原始信号
y = fft(x);    %对原始信号做FFT变换
M = abs(y);  %求FFT转换结果的模值
plot(n, M); %绘制FFT转换模值的曲线
运行代码，输出结果如下：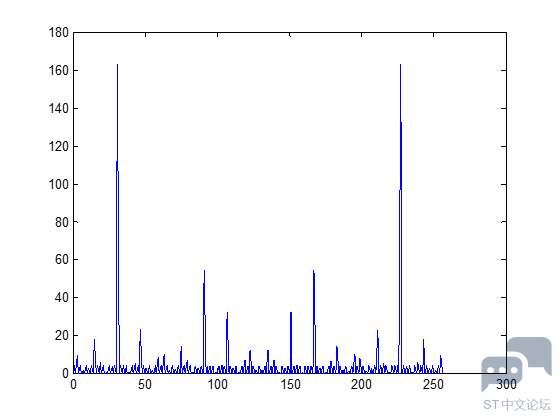

与方波的理论计算值相比，上面的幅频响应图中出现了很多小毛刺，其实这个就是频谱泄露的结果导致的。

下面就说说什么是频谱泄露：

对于频率为fs的正弦序列，它的频谱应该只是在fs处有离散谱。但是，在利用DFT求它的频谱做了截短，结果使信号的频谱不只是在fs处有离散谱，而是在以fs为中心的频带范围内都有谱线出现，它们可以理解为是从fs频率上“泄露”出去的，这种现象称为频谱“泄露"（结合上面的例子就更形象了）。

在实际问题中遇到的离散时间序列x(n)通常是无限长序列，因而处理这个序列的时候需要将它截断。截断相当于将序列乘以窗函数w(n)。根据频域卷积定理，时域中x(n)和w(n)相乘对应于频域中它们的离散傅立叶变换X(jw)和W(jw)的卷积。因此，x(n)截矩后的频谱不同于它以前的频谱。

为了减小频谱“泄露”的影响，往往在FFT处理中采用加窗技术，典型的加窗序列有Hamming、Blackman、Gaussian等窗序列。此外，增加窗序列的长度也可以减少频谱“泄露”。

时域上乘上窗函数，相当于频域进行卷积。长度为无穷长的常数窗函数，频域为delta函数，卷积后的结果和原来一样。如果是有限矩形窗，频域是Sa函数，旁瓣电平起伏大，和原频谱卷积完，会产生较大的失真。

窗的频谱，越像delta函数（主瓣越窄，旁瓣越小），频谱的还原度越高。加窗就不可避免频谱泄漏，典型的加权序列有Hamming、Blackman、Gaussian等窗序列主要是为了降低降低旁瓣，对于降低频谱泄漏效果远不如增加窗序列的长度明显。

周期信号加窗后做DFT仍然有可能引起频谱泄露，设fs为采样频率，N为采样序列长度，分析频率为：m*fs/N（m=0，1....)，以cos函数为例，设其频率为f0,如果 f0不等于m*fs/N，就会引起除f0以外的其他m*fs/N点为非零值，即出现了泄露。

DFT作为有限长的运算，对于无限长的信号必须要进行一定程度的截断，既然信号已经不完整了，那么截断后的信号频谱肯定就会发生畸变，截断由窗函数来完成，实际的窗函数都存在着不同幅度的旁瓣，所以在卷积时，除了离散点的频率上有幅度分量外，在相邻的两个频率点之间也有不同程度的幅度，这些应该就是截断函数旁瓣所造成的。

26.4 总结
通过本章节的讲解，大家应该对FFT变换结果的物理意义应该有更深入的理解了，通过后面章节的继续会让大家有更加深入的认识。